Теорема 4.3 «Условие неразрешимости задачи ЛП»

Задача ЛП не имеет решения, если среди компонентов векторов, вводимых в базис (всех возможных векторов), нет положительных компонентов.

В этом случае невозможно найти величину Q и задача считается не разрешимой.

Теорема 4.4: «Условие вырожденности оптимального плана или его неединственности»

Пусть Х^* оптимальный план. Если среди индексных оценок небазисных векторов есть нулевая оценка, а среди коэффициентов разложения вектора, соответствующего данной нулевой оценке по базису, есть хотя бы один положительный элемент, то существует, по крайней мере, еще один оптимальный план, на котором значение целевой функции такое же как и на данном.

Содержательно: это означает, что прямая, соответствующая целевой функции, параллельна одной из граней многогранника.

Метод искусственного базиса (М-метод).

Ранее было показано, что если среди ограничений в канонической формы содержится ровно m единичных векторов, то при положительных правых частях может быть сразу получено исходный решение (опорный план), отправляясь от которого с помощью преобразований симплекс-метода может быть получен оптимальный план или установлена неразрешимость задачи.

Но во многих задачах, приведенных к канонической форме, либо нет m единичных векторов, либо в правых частях есть отрицательные элементы. В этом случае для решения задач применяется метод искусственного базиса (M – метод). Идея: предполагается включение неотрицательных, искусственных переменных в левую часть каждого из уравнений, которые не содержат явных базисных переменных, обеспечивая получение исходного базиса. Эти переменные выполняют роль остаточных. Однако, так как они не имеют содержательного отношения к задаче, то их введение допустимо только в том случае, если соответствующая схема вычислений обеспечит получение оптимального решения, в котором эти переменные равны нулю. Для решения М-методом вводится понятие «расширенной задачи».

Расширенная задача.

Пусть требуется найти min Z=C₁X₁+…+C_nX_n при ограничениях:

a₁₁x₁+…+a_1nx_n=b₁

………………… (*)

a_m1x₁+…+a_mnx_n=b_m

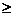x_j 0 j=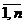

b_j>0 i=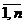

Определение: Задача, состоящая в нахождении минимума функции

F=C₁X₁+…+C_nX_n+MX_n+1+…+MX_n+m min , при ограничениях

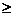x_j 0 j=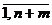

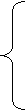a₁₁+…+a_1nx_n+x_n+1 =b₁

…………………………

a_m1x₁+a_mnx_n+…+x_n+m=b_m

где М - некоторое достаточно большое положительное число, конкретное значения которого обычно не задается, называется расширенной задачей по отношению к задаче (*).

Содержательно: Если в канонической форме задачи нет вообще единичного базиса (или он частичный), то в левой части ограничений вводится столько искусственных переменных, сколько не хватает векторов до единичного базиса, которые входят в функцию цели с коэффициентом М, конкретное значение которого может быть не задано заранее (или же его значение на 3-4 порядка больше, чем порядок коэффициента целевой функции).

В этом случае всегда существует опорное исходное решение расширенной задачи X⁰=( 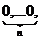b₁…b_n), которое определяется системой из n искусственных единичных векторов.

Теорема 5.1

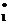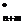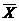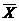
Если в оптимальном плане X*=( X … ,X ) расширенной задачи значения всех искусственных переменных равны нулю, то план *=( 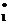, …, X ) исходной задачи является оптимальным планом исходной задачи.

Содержательно: если в найденном оптимальном плане расширенной задачи все искусственные переменные равны нулю, то имеем оптимальный план исходной задачи.

Замечание: возможна ситуация, когда в плане расширенной задачи все искусственные переменные равны нулю, но при этом он не будет оптимальным планом исходной задачи, и поэтому его следует довести до оптимального плана исходной задачи без искусственных переменных.

Исходная симплекс-таблица расширенной задачи.

Пусть X⁰=(0,…0, b₁…b_m) исходный опорный план расширенной задачи, тогда значение целевой функции f на данном плане равняется: F(X₀)=М 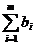, а значения оценок будут равны: Z_j-C_j=-M 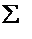a_ij-C_j , следовательно значение целевой функции и значения оценок состоит из двух частей, одна из которых содержит M, а другая нет.

Тогда в отличии от классического симплекс-метода таблица содержит две индексные строки (m+1) и (m+2). В (m+2) строку заносят коэффициент при М, а в (m+1) - часть оценки, не содержащую М.

Вычисления (пересчет симплекс-таблиц) проводятся по (m+2) строке до тех пор пока:

1. Либо все искусственные вектора не будут исключены из базиса.

2. Либо не все искусственные вектора будут исключены, но (m+2) строка не содержит больше положительных элементов, соответствующих искусственным векторам.

В первом случае базис соответствует некоторому опорному плану исходной задачи, и определение ее оптимального плана проводим только по (m+1)строке.

Во втором случае, если элемент, стоящий на пересечении (m+1) строк и столбца B отрицателен, то исходная задача не имеет решения (признак неразрешимости), а если же он равен нулю, то найденный опорный план исходной задачи является вырожденным (для данного метода), и базис содержит, по крайней мере, хотя бы один из искусственных векторов.

Если исходная задача содержит несколько единичных векторов (<m), то их следует вводить в искусственный базис; искусственных переменных столько, сколько не хватает векторов до единичного базиса.