Теорема (достаточное условие экстремума)
Пусть функция у = f(x) дифференцируема в некоторой окрестности точки х0. если в точке х = х0 производная функции f(x) равна нулю и меняет знак при переходе через точку х0, то точка х0 является точкой экстремума, причём: 1) х0 ─ точка максимума, если знак меняется с плюса на минус; 2) х0 ─ точка минимума, если знак меняется с минуса на плюс.
Теорема (достаточное условие экстремума).
Если в точке х = х0 первая производная дифференцируема в некоторой окрестности точки х0 функции у = f(x) равна нулю, а вторая производная отлична от нуля, то х0 является точкой экстремума, причём: 1) х0 ─ точка минимума, если f ''(x0) > 0; 2) х0 ─ точка максимума, если f ''(x0) < 0.
Пример.Найти экстремумы функции f(x) = 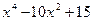 .
.
Решение. Поскольку f '(x) = 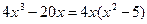 , то критическими являются только стационарные точки
, то критическими являются только стационарные точки 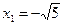 ,
, 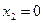 ,
, 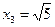 .
.
Исследуем знак второй производной f ''(x) = 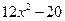 в этих точках:
в этих точках:
f ''( 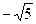 ) = 12×2 −20 > 0, f ''(0) = −20 < 0, f ''(
) = 12×2 −20 > 0, f ''(0) = −20 < 0, f ''( 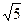 ) = 12×5 −20 > 0.
) = 12×5 −20 > 0.
Следовательно, 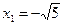 ,
, 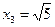 ─ точки минимума,
─ точки минимума, 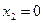 ─ точка максимума,
─ точка максимума,
причём min f(x) = f( 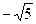 ) = f(
) = f( 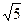 ) = -10, max f(x) = f(0) = 15.
) = -10, max f(x) = f(0) = 15.
Направления выпуклости, точки перегиба.
Определение.График функции у=f(x) называется выпуклым внизв данном промежутке, если он целиком расположен выше касательной в его произвольной точке (рис.17.7). График функции у = f(x) называется выпуклым вверхв данном промежутке, если он целиком расположен ниже касательной в его произвольной точке (рис.17.8).
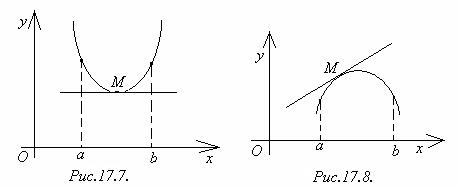
Теорема (достаточный признак выпуклости графика функции).
Если вторая производная функции у = f(x) положительна в данном промежутке, то график функции является выпуклым вниз в этом промежутке; если же вторая производная отрицательна в данном промежутке, то график функции является выпуклым вверх в этом промежутке.
Пример.Найти интервалы выпуклости графика функции f(x) = 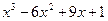 .
.
 Решение.Найдём вторую производную функции f ''(x) =
Решение.Найдём вторую производную функции f ''(x) = 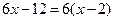 . Так как f ''(x)<0 при х < 2 и f ''(x)>0 при х > 2, то график функции является выпуклым вверх в интервале (−¥;2) и выпуклым вниз ─ в интервале (2;+¥).
. Так как f ''(x)<0 при х < 2 и f ''(x)>0 при х > 2, то график функции является выпуклым вверх в интервале (−¥;2) и выпуклым вниз ─ в интервале (2;+¥).
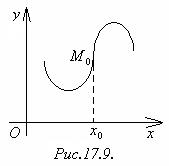
Определение. Точкой перегибаграфика функции у = f(x) называется такая его точка М0 (рис.17.9.), в которой меняется направление выпуклости.
Теорема (достаточный признак существования точки перегиба).
Если в точке х = х0 вторая производная функции у = f(x) обращается в нуль и меняет знак при переходе через неё, то М0(х0;f(x0)) ─ точка перегиба графика этой функции.
Например, в предыдущей задаче мы установили, что f ''(2) = 0 и f ''(x) меняет знак при переходе через эту точку. Следовательно, х = 2 ─ точка перегиба графика функции f(x) = 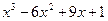 .
.
Асимптоты.
Если график функции сколь угодно близко приближается к прямой, то такую прямую называют асимптоты. Различают вертикальные и наклонные асимптоты.
Определение.Прямая х = 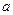 называется вертикальной асимптотойграфика у = f(x), если хотя бы одно из предельных значений
называется вертикальной асимптотойграфика у = f(x), если хотя бы одно из предельных значений 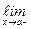 f(x),
f(x), 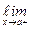 f(x) является бесконечным.
f(x) является бесконечным.
Например, прямая х = 2 ─ вертикальная асимптота графика у = 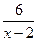 , так как
, так как 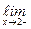
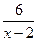 = −¥,
= −¥, 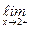
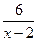 = +¥.
= +¥.
Определение.Предположим, что функция у = f(x) определена при сколь угодно больших (по модулю) значениях аргумента. Для определённости будем рассматривать положительные значения аргумента. Прямая
у = 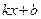
называется наклонной асимптотойграфика функции у = f(x), если эта функция представима в виде
f(x) = 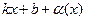 ,
,
где 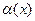 ─ бесконечно малая функция при х→ +¥.
─ бесконечно малая функция при х→ +¥.
