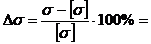Классификация активных нагрузок
1. Сосредоточенная нагрузка, задается силой F.
2. Моментная нагрузка, задается моментом М или парой сил m.
Методика решения задач на определение опорных реакций балки.
1. Выделить объект равновесия (балка).
2. Указать активные нагрузки (по классификации).
3. Указать связи и заменить их реакциями связей (шарниры или жесткая заделка).
4. Выбрать координатные оси (мысленно ось у вертикально, ось х горизонтально).
5. Составить уравнения равновесия (1 или 2 формы) и определить неизвестные реакции.
Задача 7. Определить реакции опор следующих балок:
7.1 Примечание: Активные нагрузки – сила и момент. Связь – шарниры. 2 форма равновесия
Рис.1 Расчетная схема балки
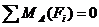
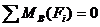
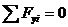
7.2 Примечание: Активные нагрузки – две силы и момент. Связь – шарниры. 2 форма равновесия
Рис.2 Расчетная схема балки
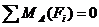
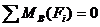
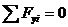
7.3 Примечание: Активные нагрузки – сила расположена симметрично относительно опор. Можно воспользоваться правилом коромысла: численное значение реакций равно половине активной нагрузки, а направление реакций противоположно направлению активной нагрузки.
Рис.2 Расчетная схема балки
YА = YВ =
7.4 Примечание: Активные нагрузки – одна сила под углом. Связь – жесткая заделка.
1 форма равновесия
Рис.1 Расчетная схема балки
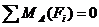
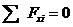
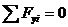
7.5 Примечание: Активные нагрузки – одна сила. Связь – жесткая заделка. 2 форма равновесия
Рис.2 Расчетная схема балки
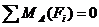
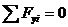
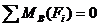
РАСЧЕТНО-ГРАФИЧЕСКИЕ РАБОТЫ ПО ТЕХНИЧЕСКО МЕХАНИКЕ
Примечание: Работы должны быть оформлены в соответствии с требованиями ГОСТ 2.105-79 и ГОСТ 2.106 -68, на листах формата А4, условия работ – с основной надписью по форме 2, решение – по форме 2а.
РГР №1 «Расчеты стержней при растяжении, сжатии»
Примечание: Для защиты модуля 1 оформить условие РГР №1 и выполнить п.п.1, 2 задачи 2.
Задача 1. Определить деформации стержней (указать в условии)
Решение: 1.1 Для стального (Е = 2٠105 МПа) стержня (рис.1) постоянного поперечного сечения (А= см2):
а) Продольные силы на участках:
N1=
N2=
N3=
N4=
б) Опасный участок: Nmax =
в) Напряжение на опасном участке:
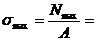
Рис.1 Расчетная схема стержня и эпюра
продольных сил
г) Удлинение стержня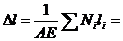 
1.2 Для стального (Е = 2٠10 5 МПа) стержня (рис.2) непостоянного поперечного сечения:
а) Продольные силы на участках:
N1=
N2=
N3= 
б) Напряжения на участках:
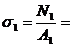
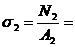
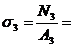
в) Опасный участок: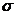 
max =
г) Удлинение стержня Рис.2 Расчетная схема бруса и
эпюры продольных сил и нормальных напряжений.
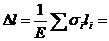
Задача 2 Для стержневой системы (рис.3) определить реакции стержней и подобрать соответствующие номера профилей (два равнополочных уголка). Определить процент пере- или недогрузки наиболее нагруженного стержня при принятых стандартных размерах сечения, если допускаемое напряжение [σ] = 150 МПа.
Рис.3 Условие задачи
Решение:
1. Определить аналитическим способом реакции в стержнях (рис.4).
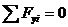
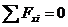
Рис.4 Расчетная схема.
2. Проверить геометрическим способом реакции в стержнях (рис.5).
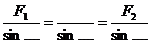
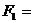
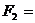
Рис.5 Расчетная схема.
3. Указать деформации стержней: 1 - 2 -
Примечание: Деформации в стержнях вызывают усилия, а они противоположны по направлению реакциям.
Далее считать F1 = N1 , F2 = N2 .
4. Определить требуемую площадь поперечного сечения для двух уголков.
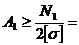
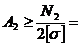
5. Подобрать номера уголков по ГОСТ 8509 – 86 Равнополочные уголки.
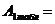см2 , № t = мм
см2 , № t = мм
6. Определить напряжение в стержнях для подобранных сечений.
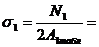
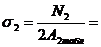
7. Определить процент перегрузки (недогрузки) наиболее нагруженного стержня.
