Некоторые комбинаторные задачи

Рассмотрим всевозможные размещения с повторениями а₁а₂ ... а_nиз n элементов с дополнительным условием: в каждом из них b₁элементов первого рода, b₂элементов второго рода и вообще biэлементов i-го рода (i = 1, 2,..., r). Естественно, выполнено равенство
b₁+ b₂+...+ br= n. Заменим biэлементов i-го рода различающимися элементами bi₁,..., bibтак, чтобы все элементы стали различными, и получим n! перестановок. Каждое исходное размещение дает b₁! • b₂! • ... • br! перестановок. Следовательно, число исходных размещений равно 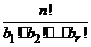, где b₁+ b₂+ … + br= n.

Это число называется полиномиальным коэффициентом: оно равно коэффициенту при произведении 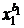• •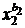. . . • 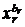в разложении по степеням переменных полинома (x₁+ x₂+...+ x_r)ⁿ.

Биномиальные коэффициенты представляют частный случай при r = 2. Другой частный случай – если все bi равны 1: число размещений всех элементов, таких что все n элементов присутствуют по одному разу, равно 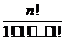= n! , т.е. числу P_nперестановок n элементов.

Пример.Общее число различных комбинаций при бросании 7 игральных костей (кубиков) равно 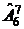= 6⁷ (при каждом бросании может выпасть любая из 6 граней). Сколько среди них таких комбинаций, что 1 и 3 выпадает дважды, 6 – трижды, а 2, 4, 5 – ни разу?

Решение дается полиномиальным коэффициентом 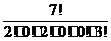= 210.

2. Пример применения принципа включения и исключения дает задача о встречах (другое название - задача о беспорядках): сколько существует перестановок а₁, а₂,..., а_nчисел 1, 2,..., n таких, что аi≠ i при любом i = 1, 2,..., n?

Обозначим это число через Dn и воспользуемся формулой (6). Здесь N элементов - это n! перестановок а₁, а₂,..., аn, а свойство Р(i) выражается равенством аi= i (i = 1, 2,..., n).
Тогда Ni₁i₂… ir= (n - r)! - число перестановок, оставляющих на месте r определенных символов.

Далее, в 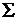Ni₁i₂… irимеется 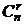слагаемых - по числу способов выбора i₁, i₂,..., i_rиз
1, 2,..., n. Применяя (6), находим, что

N(0) = n! - n • (n-1)! + 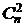• (n-2)! - . . . + (-1)r• 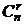• (n-r)! + . . . + (-1)n•1 =
= n! - n • (n-1)! + n • ((n-1)/2) • (n-2)! - . . . + (-1)r• (n • (n-1) • . . . • (n-r+1)/r!) • (n-r)! + . . . + (-1)n =
= n! • (1 - 1 + 1/2! - 1/3! + . . . + (-1)r/r! + . . . + (-1)n/n!).

Сумма 1 - 1 + 1/2! - 1/3! +...+ (-1)r/r! +...+ (-1)n/n!, заключенная в скобки - это частная сумма бесконечного ряда для числа е-1. Поэтому N(0), равное Dn, есть целое число, ближайшее к n!/e, т.е.

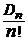≈ е-1. (10).

Вот простая интерпретация формулы (10). Если n писем для различных адресатов случайным образом разложены в n конвертах с написанными адресами, то с вероятностью, близкой к
1/е ≈ 0.368, ни один из n адресатов не получит предназначенного ему письма. Может показаться парадоксальным, однако эта вероятность практически одинакова и для 10, и для 10000 писем.

Одна из классических задач комбинаторики - определить число способов разместить некоторое множество объектов в каком-то количестве «ящиков» так, чтобы были выполнены заданные ограничения. Если даны два множества X, Y, причем ½Х½= n, ½Y½= m, то всякая функция f: X → Y задает такое размещение, если считать Х объектами, а Y - ящиками и трактовать f(xi) = yiкак помещение объекта xiв ящик yi. Другая интерпретация - раскраска: Y - множество “цветов” и f(x) - цвет объекта x. Тогда задачу можно сформулировать как определение количества раскрасок с соблюдением некоторых ограничений.

Заметим, что без потери общности можно всегда считать, что X = {1, 2,..., n}, a
Y = {1, 2,..., m}. Если не накладывать никаких ограничений на размещения, то число всех функций f: X → Y равно mn, ибо это просто (m, n)-размещения с повторениями: каждому из
n упорядоченных элементов сопоставляется один из m цветов.

Если каждый ящик содержит не более одного объекта, то мы имеем (m, n)-размещения без повторений; при этом m ≥ n. Их число равно : из m упорядоченных ящиков мы выбираем n и кладем в них по одному объекту. Если же n > m, то такое размещение, очевидно, невозможно. Здесь вступает в силу упомянутый выше принцип Дирихле.

Если мы размещаем n объектов по m ящикам так, чтобы каждый ящик содержал упорядоченную последовательность, а не просто неупорядоченное множество помещенных в него объектов, то будем называть такое размещение упорядоченным размещением n объектов по
m ящикам. Можно показать, что число таких размещений – обозначим его [m][n] – равно, полагая (для n = 0: [m][0]= 1): [m][n]= m • (m + 1) • … • (m + n – 1) = .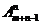

На рис. 1.2 представлены [3][2]= 3 • 4 = 12 упорядоченных размещений двух элементов a, b в трех ящиках.

Рис. 1.2

Рассмотрим некоторые алгоритмы порождения (перечисления) последовательности всех перестановок n элементов.

I. Лексикографическая (алфавитная) последовательность определяется индуктивно: для каждой перестановки указан первый элемент, далее - все следующие за ним.

1 + (все перестановки из {2,..., n} в алфавитном порядке)

2 + (все перестановки из {1, 3,..., n} в алфавитном порядке)

3 + (все перестановки из {1, 2, 4,..., n} в алфавитном порядке)

......................

k + (все перестановки из {1, 2,..., k - 1, k + 1,..., n} в алфавитном порядке)

......................

n + (все перестановки из {1, 2,..., n - 1} в алфавитном порядке).

Пример. Для n = 3:

1, 2, 3

1, 3, 2

2, 1, 3

2, 3, 1

3, 1, 2

3, 2, 1

II. Перестановки располагаются в такой последовательности, что каждая (начиная со второй) отличается от предыдущей тем, что в ней поменялись местами ровно два элемента (такая ситуация и вместе с тем операция такой замены называется транспозицией). Такая последовательность перестановок может оказаться полезной, если при решении какой-то (например, комбинаторной) задачи с каждой перестановкой связаны некоторые вычисления и существует возможность использования частичных результатов, полученных для предыдущей перестановки, если последовательные перестановки мало отличаются друг от друга.

Существуют различные алгоритмы построения таких последовательностей, удобные в тех или иных отношениях, в частности для программирования.

III. Частным случаем предыдущего можно считать последовательность, в которой разница между двумя соседними перестановками еще меньше: они различаются транспозицией
двух соседних элементов. Идея такого алгоритма - индуктивное построение. Пусть уже построена обладающая этим свойством последовательность элементов 1, 2,..., (n - 1). Тогда требуемую последовательность перестановок элементов 1, 2,..., n получим, вставляя n всеми возможными способами (их число равно n) в каждую из перестановок элементов 1, 2,..., (n-1) на различные места, передвигая n попеременно вперед и назад (n - 1)! раз. На рис. 1.3 идея этого алгоритма проиллюстрирована для n = 2, 3, 4; элемент n выделен жирным шрифтом; справа в каждом столбце отмечены транспозиции (соседних!) элементов 1, 2,..., (n - 1), при том что элемент n остается на месте.

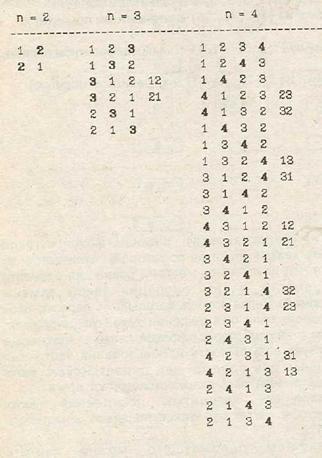
Рис. 1.3.

ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ

Представления графов

Граф – это система некоторых объектов вместе с некоторыми парами этих объектов, представляющая отношения связи между ними. Графами удобно изображаются сети коммуникаций, дискретные многошаговые процессы, бинарные отношения, химические структурные формулы, различные схемы и диаграммы и др.

Графом называется система G = (V, E), состоящая из множества элементов V = {v}, называемых вершинами графа и множества элементов E = {e}, называемых ребрами, причем каждому ребру е Î Е поставлена в соответствие упорядоченная либо неупорядоченная пара элементов v₁, v₂Î V, называемых концами ребра е = (v₁, v₂).

Объединение V È E образует множество элементов графа; при этом предполагается, что
E Ç V = Æ. Ребро находится в отношении инцидентности с каждым из своих концов. По количеству элементов графы делятся на конечные и бесконечные. Мы будем здесь рассматривать, в основном, конечные графы.

Для наглядности граф часто представляют в виде геометрического объекта: вершинам соответствуют различные выделенные точки в пространстве (на плоскости), ребрам – отрезки кривых, связывающие соответствующие точки и не проходящие через выделенные точки, отличные от их концов. Кроме того, предполагается, что кривые попарно не пересекаются во внутренних точках. Такое представление графа называется реализацией. Таким образом, граф – совокупность вершин и ребер: каждое ребро связывает две вершины (его концы), может быть, совпадающие.

Если (v₁, v₂) – упорядоченная пара вершин (т.е. (v₁, v₂) ¹ (v₂, v₁) при v₁¹ v₂), то ребро е называется ориентированным(дугой), исходящей из вершины v₁и входящей в вершину v₂;
v₁называется началом, а v₂– концом дуги e. Если (v₁, v₂) – неупорядоченная пара, то ребро e называетсянеориентированным. Если все ребра графа ориентированные, то граф называется ориентированным; если все ребра неориентированные, то и граф – неориентированный. В общем случае граф может содержать как ориентированные, так и неориентированные ребра: в этом случае – граф частично ориентированный.

Всякому графу G можно поставить в соответствие соотнесенный неориентированный граф с теми же множествами V и E и инцидентностями, но все пары неупорядоченные.

Вершина, не инцидентная ни одному ребру, называется изолированной. Вершина, инцидентная ровно одному ребру, и само это ребро называются концевыми, или висячими. Ребро с совпадающими концами называется петлей. Две вершины, инцидентные одному и тому же ребру, называются соседними, или смежными. Два ребра, инцидентные одной и той же вершине, называются смежными. Ребра, которым поставлена в соответствие одна и та же пара вершин, называются кратными, или параллельными.

Одному и тому же объекту можно сопоставить граф по-разному. Так, фрагмент дорожной сети может быть представлен неориентированным ребром, изображающим наличие связи между его концами (населенными пунктами, городскими площадями или перекрестками); одной или
двумя дугами, передающими одностороннее или двустороннее движение транспорта; несколькими дугами – отдельно для каждого ряда движения. Ребрам могут быть приписаны также числа, означающие длину, рядность, уклон и другие численные или иные характеристики.

Часто бывает важно определить, какие графы считаются различными, а какие не различаются. Обычно это связывают с понятием изоморфизма графов. Два графа G₁ = (V₁, E₁) и G₂ = (V₂, E₂) называются изоморфными, если существуют взаимно однозначные отображения f: V₁® V₂ и
g: E₁® E₂, сохраняющие инцидентность. Изоморфизм графов есть пример отношения эквивалентности.

Пример. Графы G₁ и G₃ на рис. 2.1 изоморфны. Проверьте, что соответствие

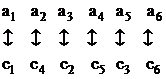
сохраняет инцидентность (a₁смежна с a₂, a₄, a₆; c₁смежна с c₄, c₅, c₆). В то же время граф G₂ не изоморфен им: достаточно заметить, что вершины b₁, b₅, b₆попарно смежны (ребра образуют треугольник), а в G₁и G₃ треугольников нет.

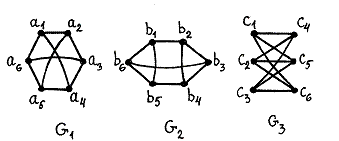
Рис. 2.1

Во многих случаях можно рассматривать графы с точностью до изоморфизма, т.е. не различать изоморфные графы; однако, если какие-то вершины или ребра графов обладают различной индивидуальностью, например, они занумерованы или им сопоставлены какие-либо численные характеристики (вес ребра, длина ребра и др.), то естественно при сравнении двух графов эту индивидуальность учитывать.

Существует несколько способов задания графов, связанных с различной формой задания инцидентности вершин и ребер. Вот некоторые из них для конечных графов.

I. Перечисление (список) ребер графа с указанием их концов и добавлением списка изолированных вершин.

Пример. Неориентированный граф G₁ (см. рис. 2.1) состоит из 6 вершин и 9 ребер: (a₁, a₂),
(a₁, a₄), (a₁, a₆), (a₂, a₃), (a₂, a₅), (a₃, a₄), (a₃, a₆).

II. Матрица инциденций графа с b вершинами и p ребрами- прямоугольная матрица
A = || aij|| с b строками и p столбцами, строки которой соответствуют вершинам графа, а столбцы - ребрам, причем для неориентированного графа элемент матрицы aijравен 1, если вершина viи ребро ejинцидентны, и равен 0 в противном случае. Для ориентированного графа aij= -1, если
viявляется началом дуги ej, и aij= +1, если vi- конец дуги ej. В каждом столбце матрицы инциденций - два ненулевых элемента, если ребро - не петля. Петле соответствует элемент, равный 2.

III. Матрица соседства (смежности) вершин графа с b вершинами- квадратная матрица
В = || bij|| размерности b, строки и столбцы которой соответствуют вершинам графа, причем неотрицательный элемент bijравен числу ребер, идущих из вершины viв вершину vj(bijне равно, вообще говоря, bji, однако для неориентированных графов матрица соседства – симметричная относительно главной диагонали матрицы). Для несмежных вершин соответствующий элемент матрицы равен 0.

Если матрица инциденций задает граф однозначно, то матрица соседства вершин определяет граф с точностью до замены любого неориентированного ребра парой противоположно направленных дуг между теми же вершинами. Однако для графов без кратных ребер задание графа и этой матрицей однозначно, элементы матрицы соседства равны в этом случае 0 или 1.

Бинарное отношение можно изобразить графом, сопоставив элементам множества вершины, а парам (a, b) Î R – ребра, связывающие a и b. Матрица отношения при этом является матрицей соседства вершин соответствующего графа.

Примеры. 1. Для отношений 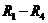, рассматривавшихся в п. 4.1. Юниты 1, соответствующие графы – на рис. 2.2.

Матрицы отношений :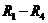

, , , .

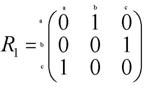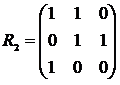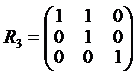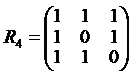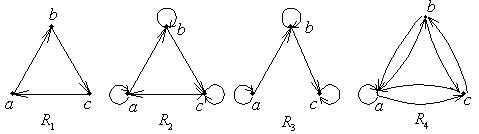
Рис. 2.2

2. Рассмотрим отношение частичного порядка T(X, Y) на множестве непустых слов в некотором алфавите: «слово Y получено вычеркиванием одной буквы из слова Х».

Например, слова abcbиabbнаходятся в отношении Т. Ориентированный граф отношения T(X, Y) на множестве слов, которые можно получить из слова abcbитерацией (т.е. многократным повторным применением) данной процедуры – на рис. 2.3.

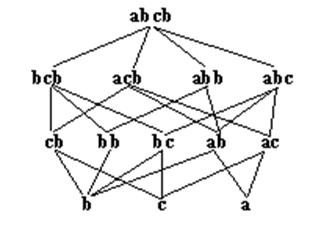
Рис. 2.3

Всякий граф с конечным (и даже счетным) числом элементов может быть реализован в трехмерном пространстве, причем, если граф не содержит кратных ребер, то ребра можно реализовать прямолинейными отрезками. На плоскости реализуется не всякий граф, что порождает разделение графов на плоские и неплоские. Тем не менее даже неплоский граф бывает удобно изображать на плоскости, надо только отличать вершины от пересечений ребер на рисунке (например, изображать вершины кружками); ориентацию ребер показывают стрелками.

Если представить графом уличную (дорожную) сеть, где ребра изображают отрезки дорог, связывающие соседние вершины (площади и перекрестки), то для небольшого населенного пункта такой граф может быть плоским, но для города с путепроводами, мостами и транспортными развязками в разных уровнях он скорее всего не плоский.

На рис. 2.4 изображен граф с 8 вершинами и 11 ребрами и проиллюстрированы некоторые введенные понятия: ребра e₁, e₃, e₆, e₇, e₉, e₁₀ являются дугами; v₆– изолированная вершина;
e₄и e₅– параллельные ребра; е₆, е₇, е₈, е₉ – также параллельные ребра, e₁₁– петля; v₂ и v₃, v₂ и
v₄– пары соседних вершин; e₃ и e₄– пара смежных ребер.

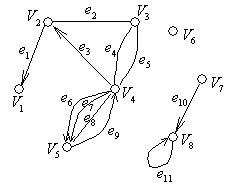
Рис. 2.4

А - матрица инциденций, В - матрица соседства вершин этого графа:

4. Рассмотрим несколько примеров графов, имеющих интересные применения.

(1) Полным графом называется граф без кратных ребер (и иногда без петель), в котором любые две вершины соединены одним ребром (ориентированным или неориентированным). Полный неориентированный граф с b вершинами без петель обозначается К_b. Очевидно, граф К_bсодержит 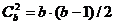ребер. Полный ориентированный граф иногда называют турниром, поскольку он отражает результат состязания по круговой системе в один круг.

На рис. 2.5, а, б, в изображены графы К₃, К₄, К₅.На рис. 2.5, г граф К₅представлен с мини-мальным числом пересечений изображений ребер (устранить их полностью нельзя: К₅– неплоский граф).

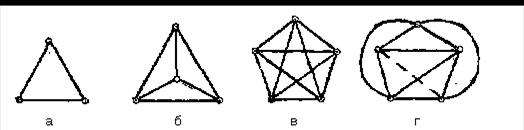
Рис. 2.5

(2) Двудольнымграфом называется граф, вершины которого разбиты на два непересекающихся класса: V = 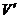È 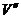, а ребра связывают вершины только из разных классов – не обязательно все пары (рис. 2.6: 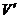= {v₁, v₂, v₃}, 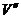= {v₄, v₅, v₆, v₇}). Какое-либо соответствие Г между непересекающимися множествами M и N можно представлять как двудольный граф с множеством вершин M È N и ребрами, связывающими каждый элемент а множества М с его образом при соответствии Г, т.е. со всеми элементами множества N, поставленными в соответствие элементу а.

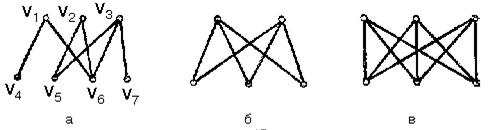
Рис. 2.6

Пример(см. п. 2.1 Юниты 1). При составлении комплекта из 40 вариантов для тестирования используется 150 задач. Каждый вариант включает 25 различных задач. Обратно, каждая задача соответствует нескольким вариантам, в которых она присутствует.

Это соответствие изображается графом с 150 вершинами в одном классе и 40 вершинами в другом; каждая из вершин второго класса соединена ребром с 25 различными вершинами первого класса.

Если же в двудольном графе каждая из вершин класса связана ребром с каждой вершиной класса , то граф называется полным двудольным и обозначается K_m,n, где m = | |, n = | |. Очевидно, граф K_m,nсодержит (m + n) вершин и m · n ребер. На рис. 2.6 изображены различные двудольные графы, в частности, на рис. 2.6, б,в – полные двудольные графы К_3,2и К_3,3 (последний носит название «3 дома – 3 колодца», ср. граф G₃ на рис. 2.1).

Упражнение.Изобразите граф К_3,3с минимально возможным числом пересечений.

(3) n-мерным единичным кубом называется граф Еn, вершинами которого являются все наборы длины n из нулей и единиц, а ребра соединяют вершины, различающиеся ровно в одной компоненте. Случаи n = 3 и n = 4 представлены на рис. 4.7, 4.8, 4.9 Юниты 1.

Упражнение. Докажите, что графы Еnявляются двудольными (указание: рассмотрите наборы с различным числом единиц).

Связные графы

Часть графа называется подграфом, если она является графом, т.е. вместе с каждым ребром в подграф должны включаться оба конца ребра.

Иногда рассматриваются только подграфы без изолированных вершин или только подграфы, содержащие все вершины графа (и только часть ребер); такие подграфы полностью определяются множеством своих ребер. В этих случаях можно естественным образом определить теоретико-множественные операции над подграфами: пересечение, объединение, симметрическую разность (называемую также суммой по модулю 2 или просто суммой), дополнение до всего графа. Подграфом, натянутым на множество вершин V¢ Í V графа G, называется подграф, содержащий вершины из V¢ и все ребра графа G, соединяющие пары вершин из V¢.

Подграф Z_a, состоящий из всех ребер, инцидентных вершине a, называется звездой вершины a. Для графов без петель степень s(a) вершины a есть число ребер в звезде Z_a. Очевидно, что сумма степеней всех вершин графа без петель равна удвоенному числу ребер (каждое ребро принадлежит двум звездам).

Для графа, изображенного на рис. 2.4, s(v₁) = 1, s(v₂) = s(v₃) = 3, s(v₄) = 7, s(v₆) = 0.

Если все вершины графа имеют одинаковую степень s (такой граф называют однородным), то сумма степеней его вершин равна b · s, а число ребер равно b · s / 2.

Упражнение. Определите число ребер в полном графе К₇ и полном двудольном К_7,5.

В графе естественным образом определяется понятие пути ‑ это последовательность ребер графа, образующая непрерывную траекторию по ребрам и вершинам графа, согласованную с ориентацией ребер. Более точно, путем [v₀, v_n] из вершины v₀ в вершинуv_nназывается последовательность вершин и ребер графа G

v₀e₁v₁e₂v₂. . .v_n-1e_nv_n , (*)

если e_k= (v_k-1, v_k) для k = 1, 2,..., n, т.е. ребро e_kориентировано из вершины v_k-1к вершине v_k или является неориентированным. Вершина v₀называется началом, а v_n– концом пути; число n называется длиной пути (путь нулевой длины состоит из одной вершины). В общем случае среди вершин и ребер последовательности (*) могут быть повторения. Говорят, что путь [v₀, v_n] прохо-дит последовательно через вершины v₀, v₁,..., v_n по ребрам e₁, e₂,..., e_n.

Путь проходит по ориентированным ребрам только в направлении ориентации, а по неориентированным – в любом направлении. При этом по одному и тому же ребру путь может проходить несколько раз. Для графа без кратных ребер путь можно задавать последовательностью проходимых вершин.

Цепью называется последовательность вершин и ребер, образующая путь в соотнесенном неориентированном графе. Отсюда всякий путь является цепью, обратное верно только для неориентированных графов, в которых понятия пути и цепи совпадают. Если последовательность (*) - цепь, то, очевидно, и ее обращение v_nenv_n-1e_n-1... e₁v₀(т.е. запись в обратном порядке) - цепь. В дальнейшем эти цепи различать мы не будем и будем говорить о цепи между вершинами v₀и v_n.

Длина пути (или цепи) определена выше как число входящих в него ребер. В более общем смысле ребрам графа могут быть приписаны числовые значения, называемые весом, или длиной ребра. Тогда длиной пути (цепи) называют сумму длин составляющих ребер. Путь или цепь [a, b] с минимальной длиной среди всех, связывающих эти вершины, называют кратчайшими.

Если в последовательности (*) v₀= v_nи n > 0, т.е. начальная вершина совпадает с конечной, то такой путь (соответственно, цепь) называется контуром (соответственно, циклом)длины n. Контур (цикл) не имеет особо выделенной вершины и может быть записан в виде последовательности (*), начиная (и заканчивая) любой его вершиной. Для неориентированного графа направление прохождения цикла не существенно. Так, для графа на рис. 2.6, а циклы
[v₂, v₅, v₃, v₆, v₂] и [v₃, v₅, v₂, v₆, v₃] совпадают.

Путь, цепь, контур, цикл называются простыми (соответственно, элементарными), если каждое их ребро (соответственно каждая вершина и каждое ребро) входит в последовательность (*) ровно один раз (не считая последней вершины в записи цикла). Простой путь не проходит дважды ни по одному своему ребру, но может повторно пересекать вершину; элементарный путь не проходит дважды ни через одну вершину.

Элементарные путь, цепь, контур, цикл можно считать некоторыми подграфами графа G.

Для графа, изображенного на рис. 2.4, цепь [v₁e₁v₂e₃v₄e₅v₃e₄v₄e₆v₅] является простой, но не элементарной (вершина v₄ встречается дважды), и не является путем (ребра e₁ и e₆имеют противоположные направления); [v₄e₃v₂e₂v₃e₅v₄] – элементарный контур.

В последовательности (*) ребро может повторяться только тогда, когда в ней повторяется некоторая вершина или когда последовательность (*) имеет такой вид:

v₀e₁v₁e₁v₀. (**)

Если цепь [v₀, v_n], отличная от (**), не является элементарной, то некоторая вершина v входит в последовательность (*) хотя бы дважды. Часть последовательности (*) между этими
двумя вхождениями вершины v есть цикл, и после вычеркивания этой части из последовательности (*) остается цепь с теми же концами v₀и v_n. Повторяя эту операцию пока возможно, мы получим в результате элементарную цепь или цепь вида (**), которую можно заменить одной вершиной. То же можно сделать с простым циклом. Тем самым устанавливаются следующие свойства цепей:

- всякая цепь [v₁, v₂] содержит элементарную подцепь с теми же концами;

- простая, но не элементарная цепь содержит элементарный цикл;

- простой цикл, проходящий через ребро e (соответственно, вершину v), содержит элементарный подцикл, проходящий через e (соответственно, v).

Таким же способом устанавливаются аналогичные утверждения для пути и для контура.

Легко видеть, что для любого графа отношение между вершинами «быть связанными цепью» есть транзитивное замыкание отношения соседства; оно является рефлексивным (вершина сама представляет собой цепь нулевой длины), симметричным (направление цепи не имеет значения) и транзитивным (склейка, т.е. последовательное прохождение цепей [a, b] и [b, c] дает цепь [a, c]). Таким образом, это отношение есть отношение эквивалентности. Вершины графа разбиваются на классы эквивалентности. Подграфы, натянутые на эти классы вершин, называются компонентами связностиграфа (или связными компонентами). Любые две вершины из
одной связной компоненты соединены хотя бы одной цепью, вершины же из разных компонент не связаны цепью. Граф на рис. 2.4 имеет 3 связные компоненты, одна из них состоит только из одной изолированной вершины v_6.

Граф называется связным, если он имеет ровно одну компоненту связности, т.е. если любые две его вершины связаны цепью. Компоненты связности любого графа G являются максимальными (по включению) связными подграфами графа G, т.е. если к связной компоненте добавить некоторое множество вершин и/или ребер, ей не принадлежащих, то полученный подграф будет несвязным. Для решения многих задач достаточно рассматривать только связные графы в том смысле, что задача для несвязного графа сводится к рассмотрению его отдельных компонент связности.

Чтобы проверить, что граф (заданный перечнем ребер или одной из матриц) связен, достаточно построить связную компоненту произвольно выбранной его вершины. Для этого, перебирая множество ребер, присоединим к этой вершине сначала смежные с ней, затем - смежные с присоединенными и т. д., пока этот процесс можно продолжать. Если все вершины графа окажутся присоединенными, граф связен; иначе - подграф, натянутый на построенное множество вершин, образует связную компоненту, и можно продолжить процесс с оставшимися вершинами, чтобы выделить все компоненты связности.

На множестве вершин V связного графа можно ввести расстояние. Для каждой пары вершин расстояние d(v₁, v₂) равно длине кратчайшей цепи, связывающей v₁и v_2. Очевидно, минимум достигается на элементарных цепях. Для d(v₁, v₂₎ выполнены три свойства расстояния:

1) d(v₁, v₁) = 0; d(v₁, v₂) > 0 при v₁≠ v₂;

2) d(v₁, v₂) = d(v₂, v₁) - симметрия;

3) d(v₁, v₂) + d(v₂, v₃) ≥ d(v₁, v₃) - неравенство треугольника.

Замечание. Если ребрам графа не приписаны числовые значения, называемые весом или длиной, то расстояние между вершинами есть число ребер в кратчайшей цепи.

Пример. В графе рис. 2.6, аимеем d(v₁, v₅) = 3; d (v₄, v₇) = 4.

Деревья

Ребро е произвольного графа G называется циклическим, если оно принадлежит хотя бы одному элементарному циклу в графе, и ациклическим в противном случае. Примером ациклического ребра является концевое, т.е. инцидентное вершине степени 1. На рис. 2.7 ребра b, d, f – циклические, ребра е, i – ациклические.

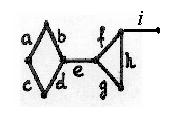
Рис. 2.7

В элементарном цикле две любые вершины связаны двумя непересекающимися (по ребрам) цепями; из одной вершины в другую можно пройти по циклу как в одну сторону, так и в другую. Поэтому при удалении из связного графа любого циклического ребра граф остается связным: в любой цепи можно заменить циклическое ребро цепью из остальных ребер цикла. С другой стороны, при удалении ациклического ребра любой граф становится несвязным: если бы граф оставался связным, то концы удаленного ребра были бы связаны элементарной цепью – возвратив удаленное ребро, получили бы элементарный цикл вопреки тому, что ребро ациклическое.

Теперь введем основное определение этого раздела. Связный граф без циклов называется деревом. Иначе говоря, дерево – это граф, все ребра которого ациклические. Имеется несколько эквивалентных определений дерева, устанавливающих ряд его характеристических свойств:

1) дерево – это связный граф, который становится несвязным при удалении любого ребра;

2) дерево – это граф, любые две вершины которого связаны единственной элементарной цепью;

3) дерево – это граф без циклов, в котором после добавления ребра, связывающего две любые вершины, появляется цикл;

4) дерево – это связный граф, у которого число ребер на единицу меньше числа вершин.

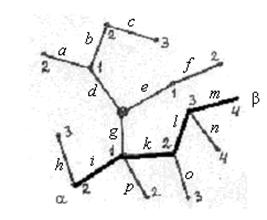
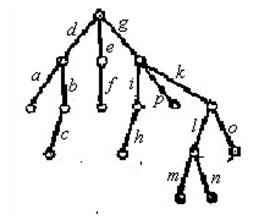
Пример дерева (рис. 2.8, а); выделены ребра единственной цепи [a, b] между вершинами a и b.

а б

Рис. 2.8

2. Рассмотрим теперь специальное представление деревьев. Выберем в дереве произвольную вершину a₀ и назовем ее корнем, или вершиной нулевого яруса. Соседние вершины назовем вершинами первого яруса и т.д., а именно вершины, соседние вершинам (i – 1)-го яруса, не отнесенные еще ни к одному ярусу, назовем вершинами i-го яруса. Каждая вершина дерева принадлежит ровно одному ярусу. Очевидно, что номер яруса совпадает с расстоянием между его вершинами и корнем дерева. В силу свойства (3) каждая вершина i-го яруса связана ребром ровно с одной вершиной (i –1)-го яруса и не связана ребром ни с какой вершиной i-го яруса. Иначе говоря, если S(a, β) – антисимметричное отношение между вершиной a и подчиненной ей вершиной β, то инверсия S^-1 отношения S – однозначное соответствие.

Пример см. на рис. 2.8, а. Выбранная (в качестве корня) вершина выделена; для остальных вершин проставлены их расстояния до корня. На рис. 2.8, б наглядное представление того же дерева с расположением вершин по ярусам. Оно показывает, в частности, что в конечном дереве всегда существуют концевые вершины (например, вершины последнего яруса, но, возможно, и другие).

Выделение корня в дереве D определяет на множестве его вершин частичный порядок: a < b, если a ¹ b и элементарная цепь из корня в вершину b содержит a (при этом ярус вершины a меньше яруса вершины b). Каждая вершина a однозначно определяет корневое поддерево D_a, натянутое на множество таких вершин b, что a £ b. Поддерево D_aполучается из своих ветвей склеиванием в корне a (рис. 2.9).

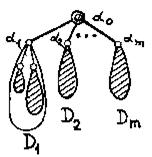
Рис. 2.9

Если каждой вершине, кроме концевых, подчинены ровно две вершины следующего яруса, то дерево называется дихотомическим. Так, турнир по олимпийской системе (с выбыванием проигравшего) изображается корневым дихотомическим деревом: корень соответствует победителю.

Замечание. Так называемое генеалогическое дерево не является, вообще говоря, деревом, так как множества предков по отцовской и материнской линиям могут пересекаться.

В п. 2.1 рассматривался ориентированный граф, изображающий отношение строгого частичного порядка на конечном множестве. Если для отношения R(X, Y) в множестве имеется наибольший элемент х_наиб, то такому отношению можно следующим образом сопоставить корневое дерево. Удалим из графа, представляющего отношение R(X, Y) транзитивные связки,
т.е. дуги (X, Y), если есть промежуточный элемент Z такой, что выполнены отношения R(X, Z) и R(Z, Y