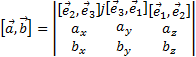Геометрические свойства векторного произведения
· Необходимым и достаточным условием коллинеарности двух ненулевых векторов является равенство нулю их векторного произведения.
· Модуль векторного произведения 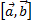 равняется площади S параллелограмма, построенного на приведённых к общему началу вектора
равняется площади S параллелограмма, построенного на приведённых к общему началу вектора 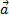 и
и 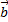
· Если 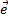 — единичный вектор, ортогональный векторам
— единичный вектор, ортогональный векторам 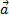 и
и 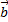 и выбранный так, что тройка
и выбранный так, что тройка 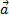 ,
, 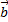 ,
, 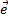 — правая, а S— площадь параллелограмма, построенного на них (приведённых к общему началу), то для векторного произведения справедлива формула:
— правая, а S— площадь параллелограмма, построенного на них (приведённых к общему началу), то для векторного произведения справедлива формула:
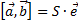
· Если  — какой-нибудь вектор, π — любая плоскость, содержащая этот вектор,
— какой-нибудь вектор, π — любая плоскость, содержащая этот вектор, 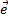 — единичный вектор, лежащий в плоскости π и ортогональный к
— единичный вектор, лежащий в плоскости π и ортогональный к 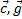 — единичный вектор, ортогональный к плоскости π и направленный так, что тройка векторов
— единичный вектор, ортогональный к плоскости π и направленный так, что тройка векторов 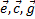 является правой, то для любого лежащего в плоскости π вектора
является правой, то для любого лежащего в плоскости π вектора 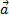 справедлива формула
справедлива формула
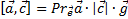
· При использовании векторного и скалярного произведений можно высчитать объём параллелепипеда, построенного на приведённых к общему началу векторах a, b и c. Такое произведение трех векторов называется смешанным.
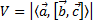
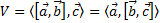
Величина векторного произведения зависит от синуса угла между изначальными векторами, поэтому векторное произведение может восприниматься как степень «перпендикулярности» векторов также, как и скалярное произведение может рассматриваться как степень «параллельности». Векторное произведение двух единичных векторов равно 1 (единичному вектору), если изначальные векторы перпендикулярны, и равно 0 (нулевому вектору), если векторы параллельны либо антипараллельны.
Алгебраические свойства векторного произведения
Далее 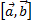 и
и 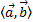 обозначают соответственно векторное и скалярное произведение векторов
обозначают соответственно векторное и скалярное произведение векторов 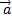 и
и 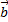 .
.
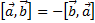 | Антикоммутативность. |
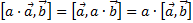 | Ассоциативность умножения на скаляр. |
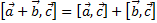 | Дистрибутивность по сложению. |
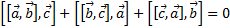 | Тождество Якоби. |
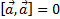 | |
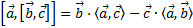 | Формула «БАЦ минус ЦАБ», тождество Лагранжа. |
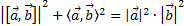 | Частный случай мультипликативности нормы кватернионов. |
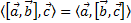 | Значение этого выражения называют смешанным произведением векторов a, b, c. |
Выражение в координатах
В правом ортонормированном базисе
Если два вектора 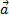 и
и 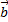 представлены в правом ортонормированном базисе координатами
представлены в правом ортонормированном базисе координатами
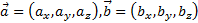
то их векторное произведение имеет координаты
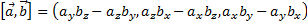
Для запоминания этой формулы удобно использовать мнемонический определитель:
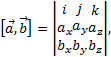
Где i=(1, 0, 0), j=(0, 1,0), k=(0, 0, 1), или
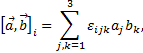
где εijk— символ Леви-Чивиты.
В левом ортонормированном базисе
Если базис левый ортонормированный, то векторное произведение в координатах имеет вид
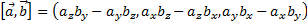
Длязапоминания, аналогично:
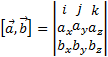
Или
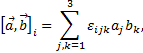
Формулы для левой системы координат можно получить из формул правой системы координат, записав те же векторы 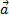 и
и 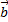 во вспомогательной правой системе координат (i′= i, j′= j, k′= −k):
во вспомогательной правой системе координат (i′= i, j′= j, k′= −k):
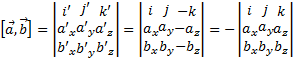
В произвольной аффинной системе координат
Векторное произведение в произвольной аффинной системе координат 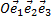 имеет координаты
имеет координаты