Главный вектор и главный момент плоской системы сил

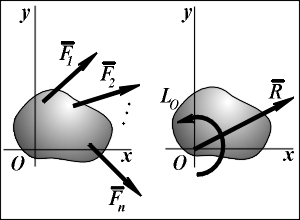Рассмотрим плоскую систему сил (F₁, F₂, ..., F_n),действующих на твердое тело в координатной плоскости Oxy.

Главным вектором системы сил называется вектор R, равный векторной сумме этих сил:

R = F₁ + F₂ + ... + F_n = 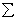F_i.

Для плоской системы сил ее главный вектор лежит в плоскости действия этих сил.

Главным моментом системы сил относительно центра O называется вектор L_O, равный сумме векторных моментов этих сил относительно точки О:

L_O = M_O(F₁) + M_O(F₂) + ... + M_O(F_n) = 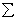M_O(F_i).

Вектор R не зависит от выбора центра О, а вектор L_O при изменении положения центра О может в общем случае изменяться.

Для плоской системы сил вместо векторного главного момента используют понятие алгебраического главного момента. Алгебраическим главным моментомL_O плоской системы сил относительно центра О, лежащего в плоскости действия сил, называют сумму алгебраических моментов этих сил относительно центра О.

Главный вектор и главный момент плоской системы сил обычно вычисляется аналитическими методами.

Главный вектор и главный момент плоской системы сил

В аналитическом методе для вычисления главного вектора и главного момента используются проекции сил F_ix, F_iy и координаты x_i, y_i точек их приложения.

Модуль R главного вектора плоской системы сил и его направляющие косинусы e_x, e_у вычисляются по следующим формулам:

R = (R_х + R_y) 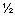; e_x = R_x / R; e_y = R_у / R; R_x = 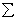F_ix; R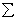_y = F_iy.

Здесь в суммировании проекций можно не включать силы, образующие пары сил (F_k, F'_k), F_k = -F'_k, поскольку суммы проекций таких двух сил на любую ось равны нулю.

Алгебраический главный момент L_O плоской системы сил относительно центра O ( начала координатных осей ) вычисляется по формуле:

L_O = 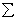(x_i F_iy - y_i F_ix) + 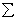M_k.

Здесь во вторую сумму выделены алгебраические моменты M_k пар сил (F_k, F'_k).

В случаях, когда плечи h_i всех сил определяются достатосно просто ( например, если силы параллельны координатным осям Ox и Oy ), величина L_O может быть вычислена по формуле:

L_O = 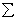± F_i h_i + 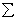M_k.

Лемма о параллельном переносе силы

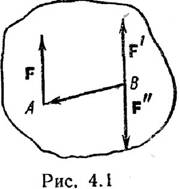
Докажем лемму: Сила, приложенная в какой-либо точке твердого тела, эквивалентна такой же силе, приложенной в любой другой точке этого тела, и паре сил, момент которой равен моменту данной силы относительно новой точки приложения. Пусть в точке А твердого тела приложена сила F (рис. 4.1). Приложим теперь в точке В тела систему двух сил F' и F²-, эквивалентную нулю, причем выбираем F'=F (следовательно, F"=–F). Тогда сила F~(F, F', F"), так как (F',F")~0. Но, с другой стороны, система сил (F, F', F") эквивалентна силе F' и паре сил (F, F"); следовательно, сила F эквивалентна силе F' и паре сил (F, F"). Момент пары (F, F") равен M=M(F,F")=BAxF, т.е. равен моменту силы F относительно точки В M=M_B(F). Таким образом, лемма о параллельном переносе силы доказана.

Основная теорема статики

Пусть дана произвольная система сил (F₁, F₂,..., F_n). Сумму этих сил F=åF_k называют главным вектором системы сил. Сумму моментов сил относительно какого-либо полюса называют главным моментом рассматриваемой системы сил относительно этого полюса.

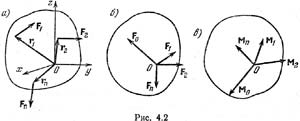
Оснтеор статики (теорема Пуансо): Всякую пространственную систему сил в общем случае можно заменить эквивалентной системой, состоящей из одной силы, прило­женной в какой-либо точке тела (центре приведения) и равной глав­ному вектору данной системы сил, и одной пары сил, момент которой равен главному моменту всех сил относительно выбранного центра приведения. Пусть О — центр приведения, принимаемый за начало коорди­нат, r₁,r₂, r₃,…, r_n–соответствующие радиусы-векторы точек приложения сил F₁, F₂, F₃, ...,F_n, составляющих данную систему сил (рис. 4.2, а). Перенесем силы F₁, F_a, F₃, ..., F_n в точку О. Сложим эти силы как сходящиеся; получим одну силу: F_о=F₁+F₂+…+F_n=åF_k, которая равна главному вектору (рис. 4.2, б). Но при последователь­ном переносе сил F₁, F₂,..., F_n в точку О мы получаем каждый раз соответствующую пару сил (F₁, F”₁), (F₂,F”₂),...,(F_n, F"_n).Моменты этих пар соответственно равны моментам данных сил относительно точки О: М₁=М(F₁,F”₁)=r₁ x F₁=М_о(F₁), М₂=М(F₂, F”₂)=r₂ x F₂=М_о(F₂), …, М_п=М(F_n, F"_n)=r_n x F_n=М_о(F_n). На основании правила приведения системы пар к простейшему виду все указанные пары можно заменить одной парой. Ее момент равен сумме моментов всех сил системы относительно точки О, т. е. равен главному моменту, так как согласно формулам (3.18) и (4.1) имеем (рис. 4.2, в) М₀=М₁+М₂+...+М_n=М_о(F₁)+М_о(F₂)+…+ М_о(F_n)==åМ_о(F_k)=år_k x F_k. Систему сил, как угодно расположенных в пространстве, можно в произвольно выбранном центре приведения заменить силой F_o=åF_k (4.2) и парой сил с моментом M₀=åM₀(F_k)=år_k x F_k. (4.3). В технике очень часто проще задать не силу или пару, а их моменты. Например, в характеристику электромотора входит не сила, с которой статор действует на ротор, а вращающий момент.