Закон больших чисел. Неравенство Чебышева. Теоремы Чебышева и Бернулли.

Закон больших чисел состоит из нескольких теорем, в которых доказывается приближение средних характеристик при соблюдении определённых условий к некоторым постоянным значениям.

Неравенство Чебышева

Если случайная величина 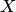имеет конечное математическое ожидание и дисперсию, то для любого положительного числа 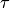справедливо неравенство

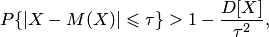
(9.1)

то есть вероятность того, что отклонение случайной величины 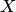от своего математического ожидания по абсолютной величине не превосходит 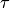и больше разности между единицей и отношением дисперсии этой случайной величины к квадрату .

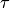Запишем вероятность события 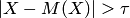, то есть события, противоположного событию 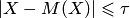. Очевидно, что

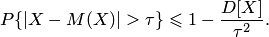
(9.2)

Неравенство Чебышева справедливо для любого закона распределения случайной величины 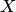и применимо как к положительным, так и к отрицательным случайным величинам. Неравенство (9.2) ограничивает сверху вероятность того, что случайная величина отклонится от своего математического ожидания на величину больше 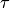. Из этого неравенства следует, что при уменьшении дисперсии верхняя граница вероятности также уменьшается, и значения случайной величины с небольшой дисперсией сосредотачиваются около её математического ожидания.

Пример 1. Для правильной организации сборки узла необходимо оценить вероятность, с которой размеры деталей отклоняются от середины поля допуска не более чем на 2 мм. Известно, что середина поля допуска совпадает с математическим ожиданием размеров обрабатываемых деталей, а среднее квадратическое отклонение равно 0,25 мм.

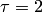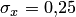Решение. По условию задачи мм и . В данном случае 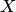— размер обрабатываемых деталей. Используя неравенство Чебышева, получаем

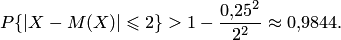
Теорема Чебышева

При достаточно большом числе независимых испытаний 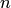с вероятностью, близкой к единицы, можно утверждать, что разность между средним арифметическим наблюдавшихся значений случайной величины 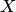и математическим ожиданием этой величины 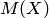по абсолютной величине окажется меньше сколь угодно малого числа 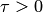при условии, что случайная величина 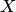имеет конечную дисперсию, то есть

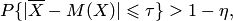
где 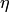— положительное число, близкое к единице.

Переходя в фигурных скобках к противоположному событию, получаем

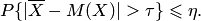
Теорема Чебышева позволяет с достаточной точностью по средней арифметической судить о математическом ожидании или, наоборот, по математическому ожиданию предсказывать ожидаемую величину средней. Так, на основании этой теоремы можно утверждать, что если проведено достаточно большое количество измерений определённого параметра прибором, свободным от систематической погрешности, то средняя арифметическая результатов этих измерений сколь угодно мало отличается от истинного значения измеряемого параметра.

Пример 2. Для определения потребности в жидком металле и сырье выборочно устанавливают средний вес отливки гильзы к автомобильному двигателю, так как вес отливки, рассчитанный по металлической модели, отличается от фактического веса. Сколько нужно взять отливок, чтобы с вероятностью более 0,9 можно было утверждать, что средний вес отобранных отливок отличается от расчётного веса, принятого за математическое ожидание, не более чем на 0,2 кг? Установлено, что среднее квадратическое отклонение веса равно 0,45 кг.

Решение. По условию задачи, имеем

,

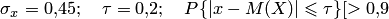где 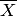— средний вес отливок гильзы. Если применить к случайной величине 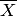неравенство Чебышева, получим

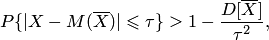
а с учётом равенств свойства математического ожидания и дисперсии средней

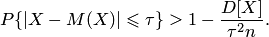
Подставляя в последнюю формулу данные задачи, получаем

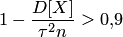, откуда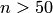

Теорема Бернулли

Теорема Бернулли устанавливает связь между относительной частотой появления события и его вероятностью.

При достаточно большом числе независимых испытаний 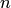с вероятностью, близкой к единице, можно утверждать, что разность между относительной частой появления события 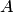в этих испытаниях е го вероятностью в отдельном испытании по абсолютной величине окажется меньше сколь угодно малого числа 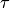, если вероятность наступления этого события в каждом испытании постоянна и равна .

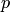Утверждение теоремы Бернулли можно записать в виде неравенства

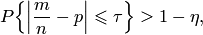
(9.3)

где 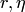— любые сколь угодно малые положительные числа.

Используя свойства математического ожидания и дисперсии, а также неравенство Чебышева, формулу (9.3) можно записать в виде

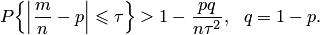
(9.4)

При решение практических задач иногда бывает необходимо оценить вероятность наибольшего отклонения частоты появлений события от её ожидаемого значения. В этом случае случайной величиной является число появления события 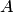в 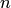независимых испытаниях. Имеем

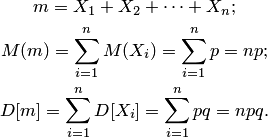
Используя неравенство Чебышева, получаем

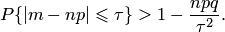
Пример 3. Из 1000 изделий, отправляемых в сборочный цех, обследованию было подвергнуто 200 отобранных случайным образом изделий. Среди низ оказалось 25 бракованных. Приняв долю бракованных изделий среди отобранных за вероятность изготовления бракованного изделия, оценить вероятность того, что во всей партии окажется бракованных изделий не более 15% и не менее 10%.

Решение. Определим вероятность изготовления бракованного изделия:

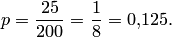
Наибольшее отклонение относительной частоты появления бракованных изделий от вероятности 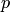по абсолютной величине равно 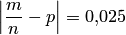; число испытаний 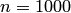. Используя формулу (9.4), находим искомую вероятность:

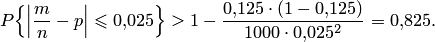
Математическая статистика. Генеральная совокупность и выборка. Случайная выборка с повторным и бесповторным отбором членов. Статистический и вариационный ряд. Полигон, гистограмма, мода, медиана выборки. Выборочное среднее, дисперсия и среднеквадратическое отклонение дискретного вариационного ряда.

Математическая статистика — это раздел математики, посвященный методам сбора, анализа и обработки статистических данных для научных и практических целей.

Статистические данные представляют собой данные, полученные в результате обследования большого числа объектов или явлений (то есть, математическая статистика имеет дело с массовыми явлениями).

Методы анализа массовых явлений — предмет многих научных дисциплин; но только в том случае, когда для анализа привлекаются формальные (абстрактные) математические модели, эти методы становятся статистическими.

Математическая статистика подразделяется на две обширные области:

описательная статистика	аналитическая статистика (теория статистических выводов)
методы описания статистических данных, представления их в форме таблиц, распределений и пр.	обработка данных, полученных в ходе эксперимента, и формулировка выводов, имеющих прикладное значение для конкретной области человеческой деятельности. Теория статистических выводов тесно связана с другой математической наукой — теорией вероятностей и базируется на ее математическом аппарате

Трудно найти современную область научных исследований, где бы ни использовались методы математической статистики. В последнее время они нашли широкое применение в медицине, биологии, социологии, т. е. в областях, сравнительно недавно считавшихся далекими от математики.

Общие положения

Понятия генеральной совокупности и выборки из нее являются основополагающими в статистике. Строгие определения заимствованы из теории вероятностей, хотя терминология этих двух наук различается. Вместо случайной величины 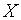в теории вероятностей, в математической статистике вводится понятие о генеральной совокупности. Под генеральной совокупностьюпонимают множество всех возможных значений случайной величины [3, 4, 9].

Вместо эксперимента (испытания, опыта), в результате которого случайная величина 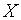приняла значение 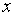(в теории вероятностей), в математической статистике вводится понятие о случайном выборе из генеральной совокупности 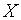значения 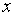. Уместная в теории вероятностей фраза «в результате 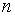независимых испытаний случайная величина 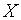приняла значения 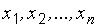» преобразуется: «случайная выборка 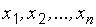объема 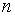извлечена из генеральной совокупности ».

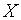Рассмотрим определения понятия «выборка», даваемые в [3, 4, 5].

Выборка – множество независимых, одинаково распределенных случайных величин.

Выборка – множество числовых значений, которые приняла исследуемая случайная величина в повторных независимых испытаниях (при этом отдельные числовые значения случайной величины в каждом испытании называются реализациями данной случайной величины, а сами испытания проводятся в неизменных условиях).

Эти два определения эквивалентны. Действительно, при рассмотрении задачи – вычисление среднего значения случайной величины Х (числа очков на грани игральной кости) – можно построить опыт двумя способами: подбрасывать один кубик много раз ( 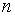раз) и вычислить среднее арифметическое по этим n реализациям (второе определение), или можно взять n одинаковых кубиков, подбросить их один раз, обеспечивая одинаковые условия испытаний (первое определение). Очевидно, значения средних арифметических, вычисленных по результатам обоих опытов, будут различны, поскольку среднее арифметическое как функция от реализаций случайной величины само является случайной величиной. А математическое ожидание как среднее по всей генеральной совокупности будет одинаковым и равным .

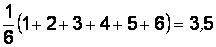Выборку можно понимать и как совокупность случайно отобранных объектов. В этом случае генеральная совокупность – совокупность объектов, из которых производится выборка. Приводя данное определение, необходимо упомянуть о повторных и бесповторных выборках. Повторная выборка производится таким образом, что отобранный объект возвращается в генеральную совокупность перед отбором следующего. При бесповторной выборке отобранные объекты не возвращаются в генеральную совокупность.

Например, для социолога, изучающего мнения избирателей перед выборами, генеральной совокупностью будет являться все население данной страны, имеющее право голоса, а выборкой объема n-множество n человек, отобранных для соответствующего опроса.

Основным предположением статистики является репрезентативность выборки, свойство выборки представлять генеральную совокупность в целом. Репрезентативность, в силу закона больших чисел, достигается случайностью отбора. Наблюдаемые значения 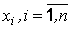, называются вариантами или опытными значениями.

Основная задача статистики – получить обоснованные выводы о характеристиках генеральной совокупности, анализируя извлеченную из нее выборку. Конкретные задачи, которые могут стоять перед исследователем статистических данных в зависимости от конкретных целей, возможностей и доступных ресурсов: описать закон распределения генеральной совокупности; подобрать значения параметров этого закона; оценить числовые характеристики генеральной совокупности; если генеральная совокупность – многомерная случайная величина, оценить всевозможные коэффициенты корреляции между ее составляющими; если есть несколько выборок, извлеченных из разных генеральных совокупностей, определить, одинаково ли распределены эти генеральные совокупности, одинаковы ли соответствующие числовые характеристики этих генеральных совокупностей и т. д.

Все перечисленные задачи сформулированы на языке математической статистики и теории вероятностей. От прикладной статистики «требуют» ответы и на другие вопросы. Можно ли утверждать, что новое лекарство излечивает эффективнее от определенной болезни, чем старое? Какой будет численность населения в следующем году? Существует ли связь между значениями предела прочности и предела текучести различных марок стали? Каковы тенденции развития фондового рынка? Существует ли исторический тренд в изменении мирового климата? и т. д. Все эти разнообразные вопросы имеют общий элемент: ответы на них зависят частично от данных. Чтобы вопросы соответствовали действительности, необходимо уметь строить адекватные вероятностные модели для реальных ситуаций, уметь представлять выборку в удобном для изучения виде, владеть математическим аппаратом теории вероятностей и математической статистики. В результате, располагая знаниями о свойствах и характеристиках изучаемой генеральной совокупности, можно предсказать свойства повторно извлеченных из нее выборок, заглянуть в будущее. Итак, анализ данных – это совокупность методов, которые помогают описать явления, определить их структуры, развить объяснения и проверить гипотезы. Он используется во всех науках, в бизнесе, управлении и политике.

Обычно численные результаты анализа выборок просты. Но анализ данных – это не анализ чисел, он лишь использует их. Анализ данных – это исследование мира в стремлении докопаться до истины.

Представление выборки

2.2.1. Вариационный ряд, таблица частот и интервальная таблица частот

В дальнейшем будет использоваться следующее обозначение выборки: 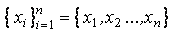, где 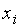– варианты выборки (опытные значения); 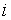– номер варианты; 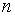– объем выборки.

Небольшие выборки удобно представлять в виде вариационного ряда. Вариационный ряд – это выборка, упорядоченная по неубыванию, т. е.

,

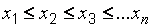в вариационном ряду представлены все значения выборки, включая повторяющиеся.

Также для представления выборок пользуются таблицами, состоящими из двух строк. В первой строке записываются варианты выборки, расположенные в порядке возрастания. Во второй строке записываются частоты или относительные частоты вариант.Частотой варианты называется число, равное количеству повторений варианты в выборке. Сумма всех частот опытных значений равна объему выборки. Таким образом, если
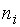– частота варианты 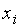, всего в выборке 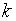разных вариант, то

,

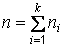где 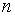– объем выборки. Относительной частотой варианты называется отношение частоты данной варианты к объему выборки:

.

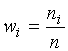Очевидно, что сумма всех относительных частот равна 1. Описанные выше таблицы называются таблицами частот итаблицами относительных частот соответственно.

Пример 2.1. С производственной линии случайным образом 36 раз отбирали по 10 единиц некоторого изделия. Каждый раз отмечалось число дефектных изделий.

Получена выборка 1:

Здесь 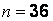(объем выборки), в выборке представлены 4 варианты: .

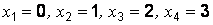Таблицу частот см. в табл. 2.1.

Таблицу относительных частот для этого примера см. в табл. 2.2.

Таблица 2.1 Таблица частот		Таблица 2.2 Таблица относительных величин

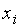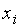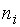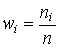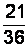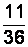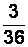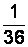Таблица относительных частот напоминает таблицу вероятностей дискретной случайной величины. Только вместо значений случайной величины пишут варианты выборки, а роль вероятностей исполняют относительные частоты. Перечень вариант выборки и соответствующих им частот или относительных частот называют также статистическим распределением выборки.

Накопленной частотой 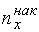называется число вариант выборки, меньших данного числа .

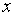Относительной накопленной частотой 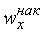называется отношение 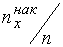. Найдем накопленные и относительные накопленные частоты

Таблица 2.3 Вариант обработки данных

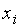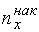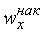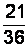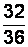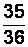вариант выборки для данного примера (табл. 2.3).

Ясно, что 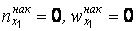, так как нет ни одной варианты, меньшей 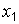.Кроме того,

;

,

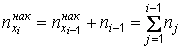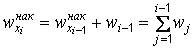отчего частоты и называются накопленными. Относительные накопленные частоты – это статистические аналоги значений функций распределения 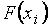дискретной случайной величины 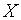. Действительно,

.

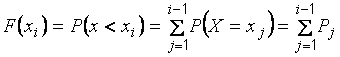Если выборка извлечена из непрерывно распределенной генеральной совокупности, причем ее объем 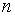достаточно велик, то такую выборку неудобно представлять в виде таблицы частот или вариационного ряда. Кроме того, при работе с непрерывно распределенными случайными величинами рассматривают не отдельные значения этих величин, а некоторые интервалы этих значений. Поэтому достаточно большую выборку, извлеченную из непрерывно распределенной генеральной совокупности, группируют по интервалам следующим образом. Весь диапазон значений вариант разбивают на разумное число интервалов, как правило, одинаковой ширины 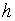. Чтобы не было недоразумений при подсчете числа вариант выборки, попавших в каждый интервал, левый конец каждого интервала считают закрытым, а правый – открытым, так что интервалы имеют вид .

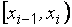Частотой i-гo интервала 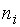называется число, равное количеству вариант выборки, попавших в этот интервал.

Относительной частотой i-гo интервала 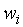называется отношение 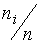. Кроме того, вычисляют накопленные и относительные накопленные частоты для правых границ интервалов.

Если рассматривается всего 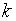интервалов, очевидно:

,

где 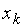– правая граница последнего интервала, все варианты выборки меньше числа .

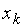Полученные числа заносят в таблицу, которая называется интервальной таблицей частот.

Пример 2.2. У 50 новорожденных измерили массу тела с точностью до 10 г. Результаты, кг, таковы (выборка 2):

3,7	3,85	3,7	3,78	3,6	4,45	4,2	3,87	3,33	3,76
3,75	4,03	3,75	4,18	3,8	4,75	3,25	4,1	3,55	3,35
3,38	3,3	4,15	3,95	3,5	3,88	3,71	3,15	4,15	3,8
4,22	3,75	3,58	3,55	4,08	4,03	3,24	4,05	3,56	3,05
3,58	3,98	3,88	3,78	4,05	3,4	3,8	3,06	4,38	4,2

Построим интервальную таблицу частот для этих данных (очевидно, что вес новорожденного является непрерывной случайной величиной). Наименьшая масса равна 3,05 кг, наибольшая – 4,75 кг, поэтому определим границы интервала [3; 4,8], который разобьем на 6 интервалов шириной 0,3.

Интервальная таблица частот выглядит следующим образом (накопленные частоты считаются для правых границ интервалов) (табл. 2.4).

Таблица 2.4

Интервальная таблица частот

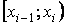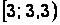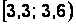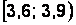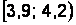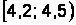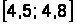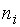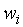	0,1	0,22	0,34	0,22	0,1	0,02
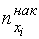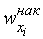	0,1	0,32	0,66	0,88	0,98	1,0