Математическое ожидание случайной величины.

Математическим ожиданием случайной величины х (M[x])называется средне

взвешенно значение случайной величины причем в качестве весов выступают

вероятности появления тех или иных значений.

Для дискретной случайной величины

_645к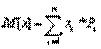

Для непрерывной

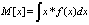
С механической точки зрения мат. Ожидание это абсцисса центра тяжести системы

точек расположенных по одноименной оси. Размерность мат. Ожидания совпадает с

размерностью самой случайной величины.

Математическое ожидание случайной величины всегда больше наименьшего значения

и меньше наибольшего.

Вероятность и числовые ряды

В схеме Бернулли снимем ограничение на конечность числа испытаний и будем "проводить" повторные испытания (как независимые, так и зависимые) неограниченное число раз.

Рассмотрим урну, в которой содержатся белые и черные шары. Проводим эксперимент, который состоит в изъятии шара из урны до тех пор, пока не будет вынут белый шар.

Пусть событие 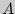= {извлечь белый шар} и 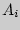= {извлечь белый шар при 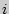-м испытании} ( 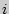=1, 2, 3, ...).

Тогда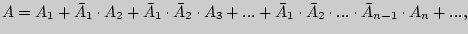

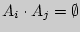
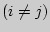
и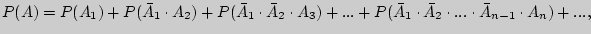

а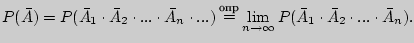

Заметим, что 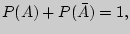и если, например, 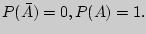Это обстоятельство используем при решении следующих примеров.

Пример 46 (сумма убывающей геометрической прогрессии). Доказать, что

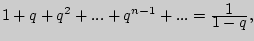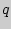где - рациональное число, удовлетворяющее неравенству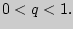

Решение 1 (вероятностное). Примем за 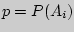и 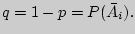Проводим повторные вынимания шара с возвратом до появления белого шара. Вероятностное дерево эксперимента имеет вид:

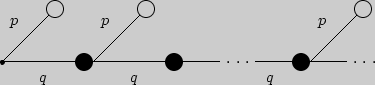
Рис. 23

Пользуясь определением суммы ряда и вероятностным деревом, получим, что

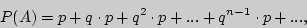
и

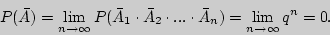
Наконец, 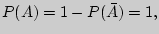отсюда получаем, что

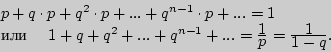
Решение 2 (геометрическое). Заполним единичный квадрат прямоугольниками, пары сторон которых лежат на сторонах квадрата, а вершинами прямоугольников выбираем соседние точки, удаленные от сторон квадрата на расстояния 1, , , ..., , , ...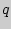

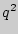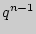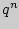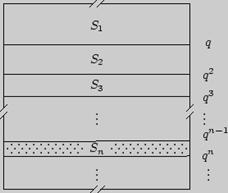
Рис. 24

Поскольку то

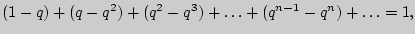
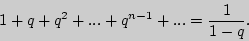
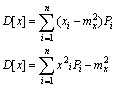16.Дисперсия Дисперсия (D[x]) характеризует рассеивание или разряженность случайнойвеличины около ее математического ожидания.Для дискретных Для непрерывных 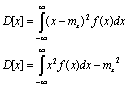Дисперсия случайной величины всегда величина положительнаяРазмерность дисперсии равна квадрату разности случайной величины Среднеквадратическое (стандартное) отклонение. 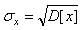Некоторые законы распределения случайных величин.Для дискретных случайных величин - биномиальное распределение и распределениеПуассонаДля непрерывных - равномерное показательное, экспоненциальное и нормальноераспределение.17.Биномиальное распределение.Биномиальным называют законы распределения случайной величины Х числапоявления некоторого события в n опытах если вероятность р появления событияв каждом опыте постоянна 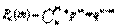Сумма вероятностей представляют собой бином Ньютона 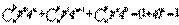Для определения числовых характеристик в биномиальное распределениеподставить вероятность которая определяется по формуле Бернули.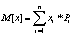 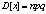При биномиальном распределении дисперсия равна мат. Ожиданию умноженному навероятность появления события в отдельном опыте. Распределение ПуассонаКогда требуется спрогнозировать ожидаемую очередь и разумно сбалансироватьчисло и производительность точек обслуживания и время ожидания в очереди.Пуассоновским называют закон распределения дискретной случайной величины Хчисла появления некоторого события в n-независимых опытах если вероятностьтого, что событие появится ровно m раз определяется по формуле. a=npn-число проведенных опытовр-вероятность появления события в каждом опытеВ теории массового обслуживания параметр пуассоновского распределенияопределяется по формулеа=λt , где λ - интенсивность потока сообщений t-времяНеобходимо отметить, что пуассоновское распределение является предельнымслучаем биномиального, когда испытаний стремится к бесконечности, авероятность появления события в каждом опыте стремится к 0. 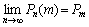Пуассоновское распределение является единичным распределением для котороготакие характеристики как мат. Ожидание и дисперсия совпадают и они равныпараметру этого закона распределения а.

18. ретье широко используемое дискретное распределение – распределение Пуассона. Случайная величина Y имеет распределение Пуассона, если

,

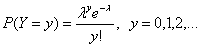где λ – параметр распределения Пуассона, и P(Y=y)=0 для всех прочих y (при y=0 обозначено 0! =1). Для распределения Пуассона

M(Y) = λ, D(Y) = λ.

Это распределение названо в честь французского математика С.Д.Пуассона (1781-1840), впервые получившего его в 1837 г. Распределение Пуассона является предельным случаем биномиального распределения, когда вероятность р осуществления события мала, но число испытаний n велико, причем np = λ. Точнее, справедливо предельное соотношение

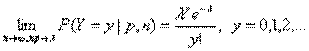
Поэтому распределение Пуассона (в старой терминологии «закон распределения») часто называют также «законом редких событий».

Распределение Пуассона возникает в теории потоков событий (см. выше). Доказано, что для простейшего потока с постоянной интенсивностью Λ число событий (вызовов), происшедших за время t, имеет распределение Пуассона с параметром λ = Λt. Следовательно, вероятность того, что за время t не произойдет ни одного события, равна e^-Λt, т.е. функция распределения длины промежутка между событиями является экспоненциальной.

Распределение Пуассона используется при анализе результатов выборочных маркетинговых обследований потребителей, расчете оперативных характеристик планов статистического приемочного контроля в случае малых значений приемочного уровня дефектности, для описания числа разладок статистически управляемого технологического процесса в единицу времени, числа «требований на обслуживание», поступающих в единицу времени в систему массового обслуживания, статистических закономерностей несчастных случаев и редких заболеваний, и т.д.

Описание иных параметрических семейств дискретных распределений и возможности их практического использования рассматриваются в обширной (более миллиона названий статей и книг на десятках языков) литературе по вероятностно-статистическим методам.

Геометрическое рапределение

Производится серия испытаний. Случайная величина - количество испытаний до появления первого успеха (например, бросание мяча в корзину до первого попадания). Закон распределения имеет вид:

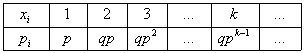
Если количество испытаний не ограничено, т.е. если случайная величинв может принимать значения 1, 2, ..., ∞, то математическое ожидание и дисперсию геометрического распределения можно найти по формулам M(X) = 1/p, D(X) = q/p²

Пример 3.2

Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель p = 0,6 при каждом выстреле. С.в. X - число возможных выстрелов до первого попадания. а) Составить ряд распределения, найти функцию распределения, построить её график и найти все числовые характеристики. б) Найти математическое ожидание и дисперсию для случая, если стрелок намеревается произвести не более трёх выстрелов.

Показать решение

Решение
а) Случайная величина может принимать значения 1, 2, 3, 4,..., ∞
P(1) = p = 0,6
P(2) = qp = 0,4 · 0,6 = 0,24
P(3) = q²p = 0,4² · 0,6 = 0,096
...
P(k) = q^k-1p = 0,4^k-1 · 0,6
...

Ряд распределения:
x_i| 1 | 2 | 3 | ... | k | ...
-----------------------------------------
p_i| 0,6 | 0,24|0,096| ... |0,4^k-1 · 0,6| ...

Контроль: Σp_i = 0,6/(1-0,4) = 1 (сумма геометрической прогрессии)
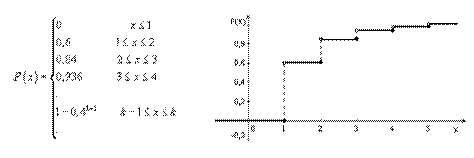
Функция распределения - это вероятность того, что с.в. Х примет значение меньшее, чем конкретное числовое значение х. Значения функции распределения определяем суммированием вероятностей.
Если x ≤ 1, то F(x) = 0
Если 1 < x ≤ 2, то F(x) = 0,6
Если 2 < x ≤ 3, то F(x) = 0,6 + 0,24 = 0,84
Если 3 < x ≤ 4, то F(x) = 0,84 + 0,096 = 0,936
...
Если k-1 < x ≤ k, то F(x) = 0,6(1-0,4^k-1)/(1-0,4) = 1-0,4^k-1 (частичная сумма геометрической прогрессии)
...

M(X) = 1/p = 1/0,6 ≈ 1,667
D(x) = q/p² = 0,4/0,36 ≈ 1,111
σ(Х) = √D(X) ≈ 1,054

б) Случайная величина может принимать значения 1, 2, 3.
P(1) = p = 0,6
P(2) = qp = 0,4 · 0,6 = 0,24
P(3) = q²p + q³ = 0,4² · 0,6 + 0,4³ = 0,16

Ряд распределения:

x_i| 1 | 2 | 3
-------------------
p_i| 0,6 | 0,24|0,16

Контроль: Σp_i = 0,6 + 0,24 + 0,16 = 1

Функция распределения.
Если x ≤ 1, то F(x) = 0
Если 1 < x ≤ 2, то F(x) = 0,6
Если 2 < x ≤ 3, то F(x) = 0,6 + 0,24 = 0,84
Если x > 3, то F(x) = 0,84 + 0,16 = 1

M(X) = 1 · 0,6 + 2 · 0,24 + 3 · 0,16 = 1,56
D(X) = 1² · 0,6 + 2² · 0,24 + 3² · 0,16 - 1,56² = 0,5664
σ(Х) ≈ 0,752

21. Случайную величину 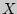будем называть непрерывной, если ее интегральная функция распределения 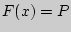{ 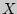< 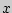} непрерывна и дифференцируема, за исключением, быть может, конечного числа точек.

Дифференциальной функцией распределения 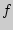называют производную от интегральной функции

'( .

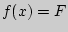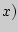Вместо термина "дифференциальная функция" используют другое название - "плотность вероятности", поскольку

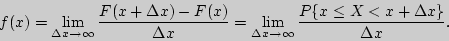
Свойства дифференциальной функции:

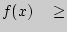0;

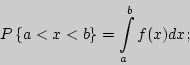
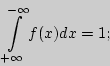
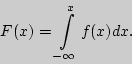
Пусть функция 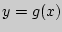монотонно возрастает и 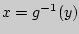- обратная функция. Тогда

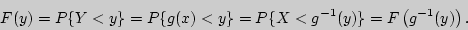
Дифференцируя это равенство по 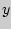, получаем (если 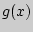дифференцируема): 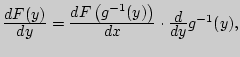т.е.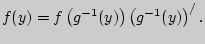

Если 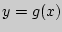монотонно убывающая функция, то аналогично получаются следующие соотношения:

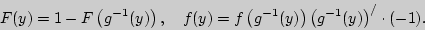
Случай, когда функция 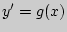является монотонно возрастающей или убывающей, имеет основное прикладное значение.

Пример 86. Закон равномерного распределения вероятностей.

Распределение вероятностей называется равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, дифференциальная функция имеет постоянное значение.

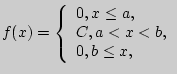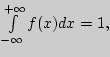Пусть т.к. то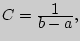

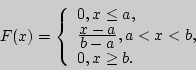
Пример 87. Показательное распределение.

Решение. Показательное распределение задается своей дифференциальной функцией

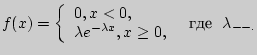
Проверим, что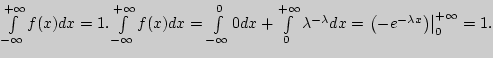

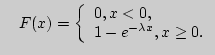
Продолжительность существования радиоактивных частиц описывается показательным распределением.

Характеристиками положения н.с.в., так же как и дискретной, являются математическое ожидание, мода и медиана.

22.О.Математическое ожидание непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством

Где f ( x ) дифференциальная функция. Предполагается, что интеграл сходится абсолютно.

В частности, если возможные значения принадлежат интервалу ( a , b ), то

О. Модой М₀(Х) непрерывной случайной величины называют то ее возможное значение, которому соответствует максимум дифференциальной функции.

О.Медианой M_e(X) непрерывной случайной величины называют то ее возможное значение, которое определяется равенством

Р ( Х < M_e(X) )=P(X> M_e(X)).

О.Дисперсия непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством

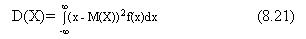
Или равносильным равенством

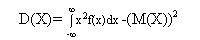
В частности, если возможные значения принадлежат интервалу ( a , b ), то

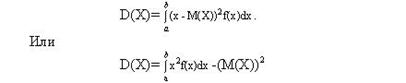
23. щее название Класса распределений вероятностей, возникающего при распространении идеи "равновозможности исходов" на непрерывный случай. Подобно нормальному распределению Р. р. появляется в теории вероятностей как точное распределение в одних задачах и как предельное - в других.

Р. р. на отрезке числовой прямой (прямоугольное распределение). Р. р. на каком-либо отрезке [ а, b], а<b, - это распределений вероятностей, имеющее плотность

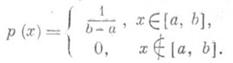
Понятие Р. р. на [ а, b] соответствует представлению о случайном выборе точки на этом отрезке "наудачу". Математич. ожидание и дисперсия Р. р. равны, соответственно, (b+a)/2 и (b-а)²/12. Функция распределения задается формулой

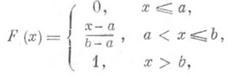
а характеристич. функция - формулой

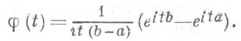
Случайную величину с Р. р. на [0,1] можно построить, исходя из последовательности независимых случайных величин Х ₁, Х ₂, . . ., принимающих значения 0 и 1 с вероятностями ¹/₂ полагая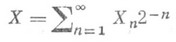

( Х _n являются цифрами в двоичном разложении X). Случайное число Xимеет Р. р. на отрезке [0,1]. Этот факт имеет важные статистич. приложения, см., напр., Случайные и псевдослучайные числа.

Если независимые случайные величины Х ₁ и Х ₂ имеют Р. р. на [0,1], то их сумма Х ₁+Х ₂ имеет так наз. треугольное распределение на [0,2] с плотностью u₂ (х)=1 -|1-х | для и u₂(x)=0 для 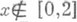. Сумма трех независимых случайных величин с Р. р. на [0,1] имеет распределение на [0,3] с плотностью

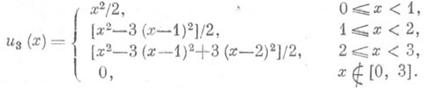
В общем случае сумма X₁+X₂+. . . +Х _n независимых величин с Р. р. на [0,1] распределена с плотностью

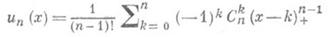
для 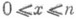и и _п (х)=0 для 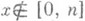; здесь

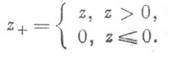
Распределение суммы нормированной математич. ожиданием n/2 и среднеквадратич. отклонением 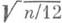, с ростом пбыстро сближается с нормальным распределением с параметрами 0 и 1 (уже при n=3 приближение удовлетворительно для многих практич. целей).

В статистич. приложениях процедура построения случайной величины с заданной функцией распределения F(х).основана на следующем факте. Пусть случайная величина Yраспределена равномерно на [0,1] и функция распределения F(х).непрерывна и строго возрастает. Тогда случайная величина 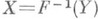имеет функцию распределения F(х).(в общем случае надо заменить в определении Xфункцию F^-1 (у).на нек-рый ее аналог, а именно ).

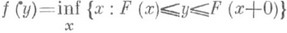P.p. на отрезке как предельное распределение. Ниже приводятся типичные примеры возникновения Р. р. на [0,1] в качестве предельного.

1) Пусть X₁, X₂, . . ., Х _n,... - независимые случайные величины, имеющие одну и ту же непрерывную функцию распределения. Тогда распределение их суммы S_n, приведенной по mod 1, т. е., иными словами, распределение дробной части {S_n} суммы S_n, сходится к равномерному на [0, 1] распределению.

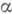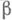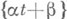2) Пусть параметры и имеют абсолютно непрерывное совместное распределение; тогда при распределение сходится к равномерному на [0,1].

3) Р. р. встречается как предельное распределение дробных долей нек-рых функций g(n) натурального аргумента п. Напр., при иррациональном a. доля тех 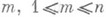, из пдля к-рых

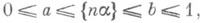
имеет пределом при величину b-а.

Р. р. на под множествах . Пример Р. р. в прямоугольнике встречается уже в Бюффона задаче (см. также Геометрические вероятности, Стохастическая геометрия]. Р. р. на нек-ром ограниченном множестве Dв евклидовом пространстве определяется как распределение, имеющее плотность

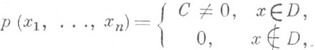
где Собратна k-мерному объему (или лебеговой мере) области D.

Рассматривают также и Р. р. на поверхностях. Так, "случайное направление" (напр., в 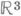) определяют вектором, идущим из начала координат в случайную точку поверхиости единичной сферы, равномерно распределенную в том смысле, что вероятность ее попадания в какую-либо часть поверхности пропорциональна площади этой части.

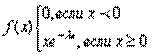24. Показательное (экспоненциальное распределение)Показательным называют распределение непрерывной случайной величины Х котороеописывается следующей дифференциальной функцией Экспоненциальное распределение для непрерывных случайных величин являетсяаналогом распределения Пуассона для дискретных случайных величин и имеетследующий вид. 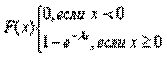вероятность попадания случайной величины Х на интервал (α;β) 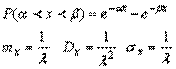Следует отметить, что время безотказной работы удовлетворяется именнопоказательному закону, а поэтому это понятие часто используется в понятиинадежности.