Математическое ожидание дискретной случайной величины.

Подойдём естественным образом к понятию математического ожидания или среднего значения принимаемого случайной величиной.

Пусть ξ – дискретная случайная величина, связанная с некоторым опытом. Предположим, что опыт осуществлен N раз и при этом величина ξ: N₁ раз принимала значение x₁, N₂ раз принимала значение х₂ и т.д. Найдем среднее арифметическое всех значений, принятых величиной ξ в данной серии опытов. Оно запишется:

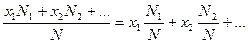
Рассмотрим событие 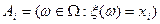тогда, в нашем случае N(A_i)=N_i и дробь 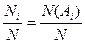есть относительная частота наступления события 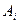(или, что то же самое, появления значения 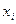) в N опытах. С увеличением числа опытов N эта дробь будет приближаться (см. §2 гл.I) к

p_i- вероятности события A_i =( ξ=x_i ).

В итоге получаем, что с увеличением числа опытов N среднее арифметическое будет приближаться к числу

x₁ 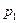+x₂ +… .

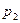Исходя из полученной формулы дадим следующее определение:

Определение: Математическим ожиданием или средним значением дискретной случайной величины с законом распределения

		(1) ...
		...

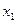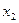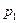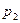называется число (обозначаемое через Mξ или )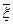

Mξ = x₁ 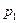+x₂ 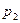+… . (2)

Другими словами, математическое ожидание ДСВ ξ равно сумме произведений возможных значений величины ξ на их вероятности.

Смысл Mξ ясен из приведённого выше рассуждения. Он заключается в том, что около числа Mξ колеблется среднее арифметическое значений, принимаемых величиной ξ в больших сериях опытов.

В случае когда ДСВ принимает бесконечное (счётное) число значений, в правой части (2) стоит сумма бесконечного ряда, к определению математического ожидания мы добавим следующее требование: ряд (2) должен сходится абсолютно. Другими словами, должен сходится ряд

|x₁|p₁+|x₂|p₂+… ,

составленный из абсолютных величин членов ряда (2). Смысл этого требования заключается в следующем. Если произвольным образом поменять местами столбцы таблицы (1), то изменённая таблица будет по прежнему задавать закон распределения величины ξ. В ряде (2) при этом произойдет перестановка слагаемых. Для того, чтобы число Mξ оставалось неизменным, нужно, следовательно, потребовать, чтобы сумма ряда (2) не менялась при любой перестановке слагаемых. Как известно, таким свойством обладают только абсолютно сходящиеся ряды. Если ряд (2) не абсолютно сходится, то среднее значение Mξ, будем говорить, не существует.

Рассмотрим ряд примеров на нахождение математического ожидания.

Пример 1. Биномиальное распределение

В этом случае

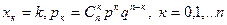(3)

Согласно (2)

Mξ =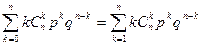

Для вычисления суммы заметим, что при k>0

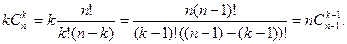
Отсюда получаем

Mξ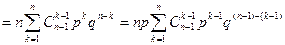

Заменим индекс суммирования к на j=k-1; когда k меняется от 1 до n, то j меняется от 0 до n-1; применяя бином Ньютона, имеем:

Mξ= .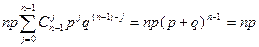

Итак, для биномиального распределения среднее значение равно np.

Например, в серии из n выстрелов, с вероятностью попадания в одном выстреле p, среднее число попаданий равно np.

Пример 2. Распределение Пуассона.

В этом случае закон распределения задается таблицей:

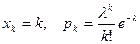, k=0,1,2,.... (4)

Отсюда имеем:

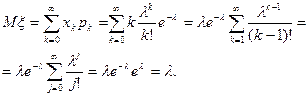
Таким образом, параметр λ, характеризующий Пуассоновское распределение, есть среднее значение величины .

Если распределение Пуассона применяется как приближённое распределение вместо биномиального с большим n (см. §12 гл. I) , то λ=np.

Пример 3. Геометрическое распределение.

В этом случае

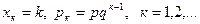(5)

Рассмотрим это распределение на примере задачи.

Проводится ряд независимых опытов, в каждом опыте с вероятностью p наступает событие А. Опыты продолжаются до первого появления события А. Случайная величина

– число произведённых опытов. Нетрудно видеть, что величина распределена по геометрическому закону (5).

Вычислим M .

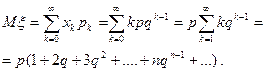
Ряд, записанный в скобках, получается почленным дифференцированием геометрической прогрессии

q+q²+ q³+ …+qⁿ +…= .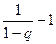

Следовательно,

.

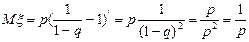Итак, среднее значение геометрического распределения равно .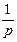

Решим важную задачу.

Задача. ДСВ ξ задана законом распределения (1). Найти математическое ожидание случайной величины η=φ(ξ), где φ некоторая функция.

Решение. Закон распределения ДСВ η=φ(ξ) мы рассмотрели в §4 гл. II.

Возможными значениями величины η будут числа

φ(x₁), φ(x₂),… .

Пусть c₁, c ₂,… различные значения φ(x_i), i=1,2,…, тогда

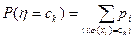
и значит

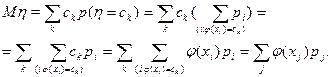
Итак, для нахождения М(φ(ξ)) мы получили формулу

М(φ(ξ))= 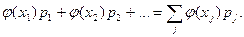(6)

Перейдём теперь к непрерывным распределениям.