Исследование функции и построение графика

Общая схема исследования функции и построения ее графика.

1.Область определения функции, поведение функции на границе области определения. Асимптоты. Точки пересечения с осями.

(Справка: для нахождения асимптот рассматриваем односторонние пределы (вертикальная асимптота), и пределы при х→∞ для выражений f(x)/х (предел равен к) и f(x)-кх (b) (наклонная асимптота у=кх+b). Подробнее вопр.1.3.

2.Четность, нечетность. Периодичность.

(справка: четная f(-x)=f(x); нечетная f(-x)=-f(x). Периодичность f(x+Т)=f(x)=f(x-Т))

3.Монотонность и экстремумы. (Функции, убывающие или возрастающие на некотором числовом промежутке, называются монотонными. Находим производную, критические точки. промежутки возрастания и убывания, точки максимума и минимума).

4.Выпуклость, вогнутость, точки перегиба. (Для этого находим вторую производную, точки перегиба, распределяем знаки второй производной: -вогнутая, +выпуклая)

5.График функции с обозначением всех найденных точек и асимптот.

Вектор-функция .Годограф.

Вектор-функция — функция, значениями которой являются векторы в векторном пространстве 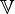двух, трёх или более измерений. Аргументами функции могут быть:

§ одна скалярная переменная — тогда значения вектор-функции определяют в 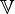некоторую кривую;

§ m скалярных переменных — тогда значения вектор-функции образуют в 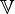, вообще говоря, m-мерную поверхность;

§ векторная переменная — в этом случае вектор-функцию обычно рассматривают как векторное поле на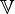

Для наглядности далее ограничимся случаем трёхмерного пространства, хотя распространение на общий случай не составляет труда. Вектор-функция одной скалярной переменной 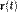отображает некоторый интервал вещественных чисел 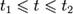в множество пространственных векторов (интервал может также быть бесконечным).

Выбрав координатные орты 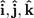, мы можем разложить вектор-функцию на три координатные функции x(t), y(t), z(t):

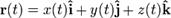
Рассматриваемые как радиус-векторы, значения вектор-функции образуют в пространстве некоторую кривую, для которой t является параметром.

Говорят, что вектор-функция 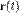имеет предел 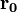в точке t = t₀, если 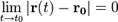(здесь и далее 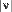обозначаютмодуль вектора 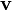). Предел вектор-функции имеет обычные свойства:

§ Предел суммы вектор-функций равен сумме пределов слагаемых (в предположении, что они существуют).

§ Предел скалярного произведения вектор-функций равен скалярному произведению пределов сомножителей.

§ Предел векторного произведения вектор-функций равен векторному произведению пределов сомножителей.

Непрерывность вектор-функции определяется традиционно

Годограф (от др.-греч. ὁδός — путь, движение, направление и γράφω — пишу) в механике — кривая, представляющая собой геометрическое место концов переменного (изменяющегося со временем) вектора, значения которого в разные моменты времени отложены от общего начала О (см. рис.).

Понятие годографа было введено английским учёным У. Гамильтоном.

Годограф даёт наглядное геометрическое представление о том, как изменяется со временем физическая величина, изображаемая переменным вектором, и о скорости этого изменения, имеющей направление касательной к годографу. Например, скорость точки является величиной, изображаемой переменным вектором v. Отложив значения, которые имеет вектор v в разные моменты времени, от начала О, получим годограф скорости; при этом величина, характеризующая быстроту изменения скорости в точке М, то есть ускорение (в этой точке), имеет для любого момента времени направление касательной к годографу скорости в соответствующей его точке М’.