Последовательное соединение R, L, С.

Основной задачей при анализе цепи синусоидального тока является расчет тока по заданному напряжению на зажимах цепи и параметрам элементов цепи. К зажимам цепи последовательно соединенных R, L и C элементов прилагаем синусоидальное напряжение (рис. 6.1) 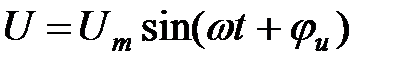. По замкнутой цепи протекает синусоидальный ток i.

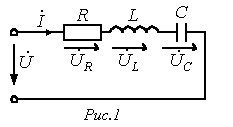
К зажимам цепи последовательно соединенных R, L и C элементов прилагаем синусоидальное напряжение 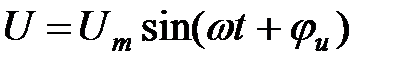. По замкнутой цепи протекает синусоидальный ток i.

По второму закону Кирхгофа напишем уравнение электрического состояния цепи:

U=U_r+U_L+U_C ,

где

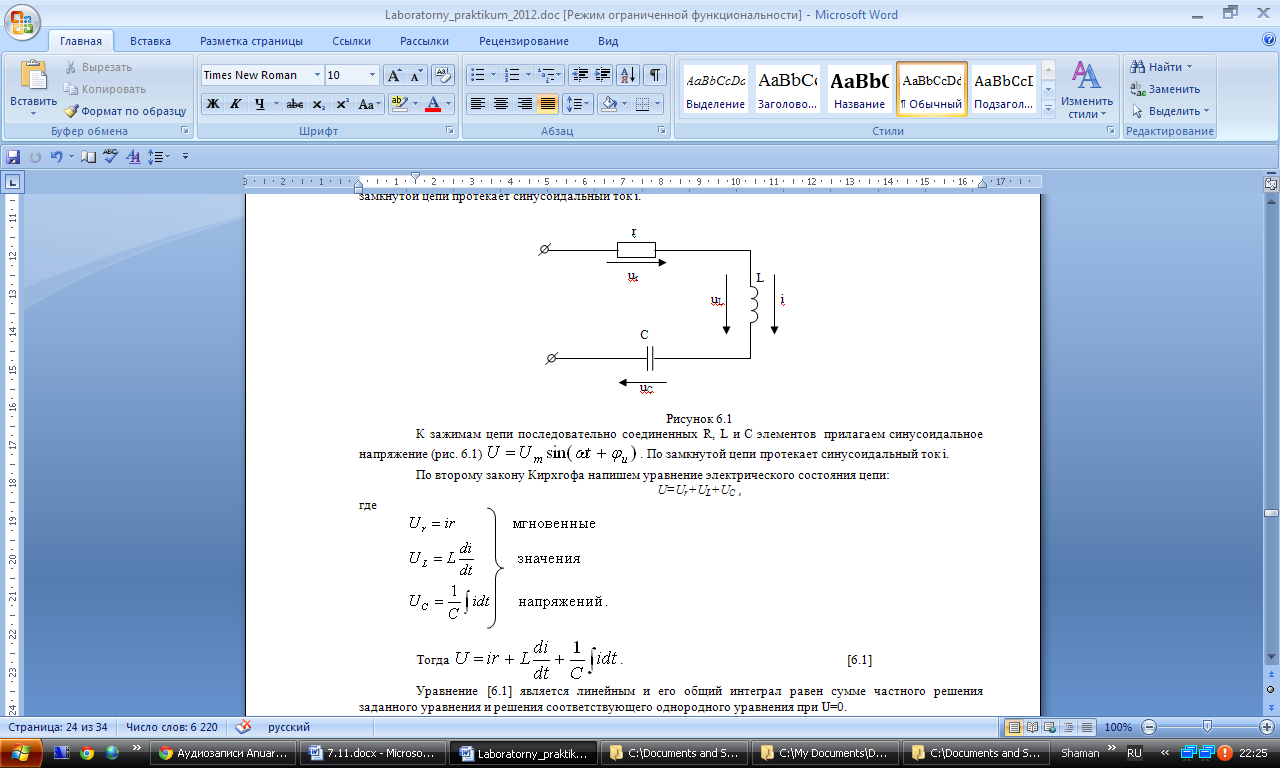
Тогда .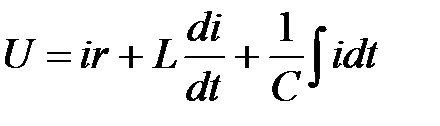

Уравнение [6.1] является линейным и его общий интеграл равен сумме частного решения заданного уравнения и решения соответствующего однородного уравнения при U=0.

Тогда решение будет иметь следующий вид:

.

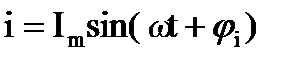Таким образом, задача сводится к определению I_m и φ (где φ=φ_u-φ_i). Проще и нагляднее задача решается с помощью векторной диаграммы, изображающей синусоидальные функции с помощью комплексных чисел.

где , , .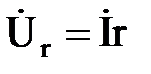

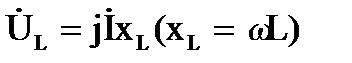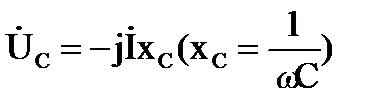После подстановки в уравнение [6.2] имеем:

.

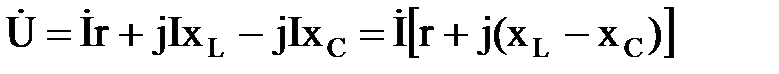Применив закон Ома, можно определить полное сопротивление цепи z:

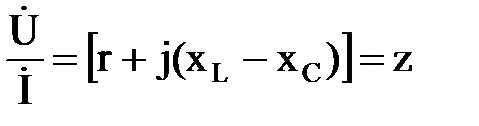
где - реактивное сопротивление цепи;

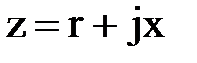- алгебраическая форма полного комплексного сопротивления цепи;

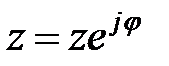показательная форма,

где 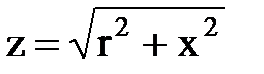, а .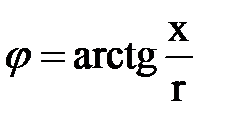

В зависимости от величины реактивного сопротивления различают три режима:

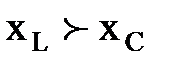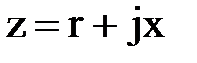1. Если , то - цепь активно-индуктивная.

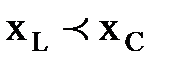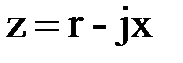2. Если , то - цепь активно-емкостная.

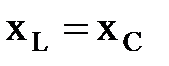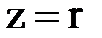3. Если , то - цепь активная.

Построение векторных диаграмм на комплексной плоскости.

Проще и нагляднее задача решается с помощью векторной диаграммы, изображающей синусоидальные функции с помощью комплексных чисел.

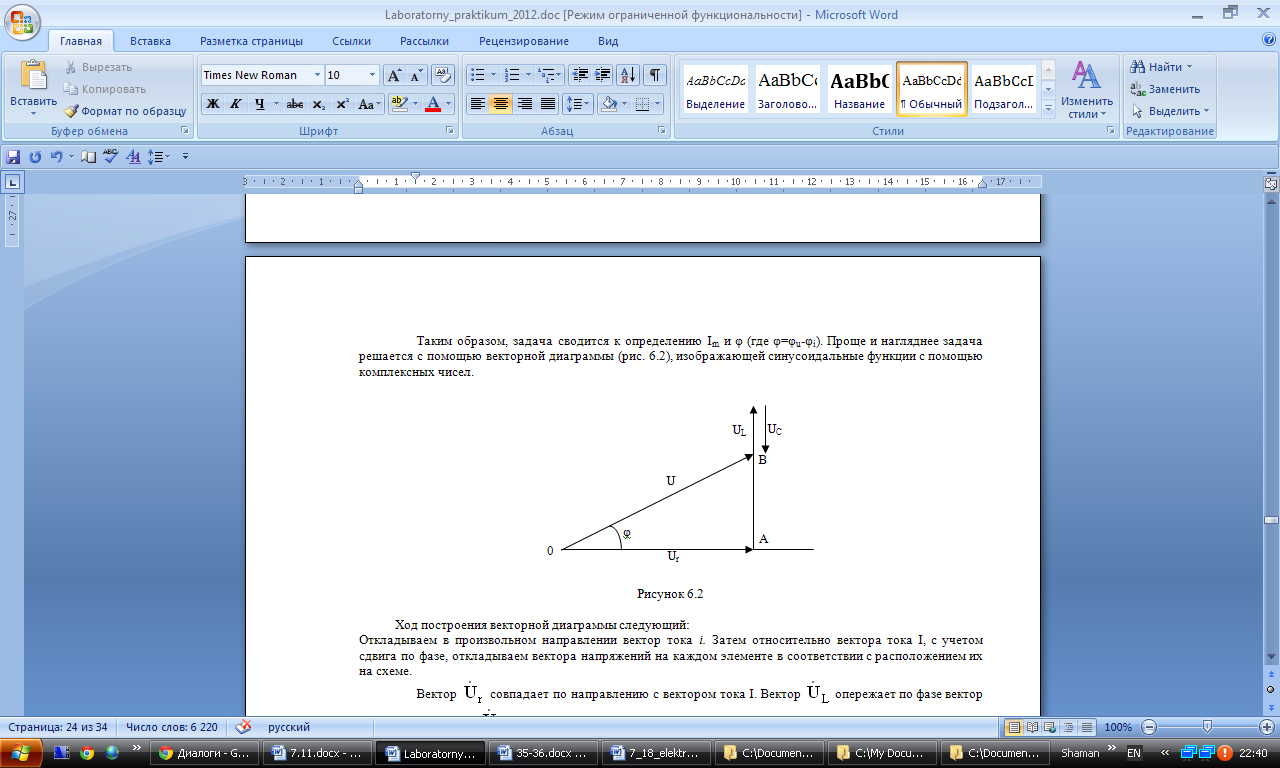
Ход построения векторной диаграммы следующий:

Откладываем в произвольном направлении вектор тока i. Затем относительно вектора тока I, с учетом сдвига по фазе, откладываем вектора напряжений на каждом элементе в соответствии с расположением их на схеме.

Вектор 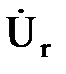совпадает по направлению с вектором тока I. Вектор 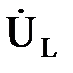опережает по фазе вектор тока на π/2, а вектор 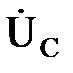отстает от вектора I на π/2.

Сумма векторов должна удовлетворять равенству U=U_r+U_L+U_C.

Из прямоугольного треугольника ОАВ, по второму закону Кирхгофа, уравнение цепи будет иметь вид:

,

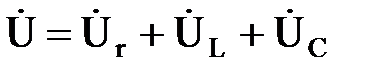Активная мощность

Потребляемая в цепи мощность равна произведению напряжения на зажимах это цепи на силу тока. При переменном напряжении это справедливо только для мгновенной мощности выражаемое через мгновенные значения напряжения и силы тока.

p=ui

Переодические изменения напряжения и силы тока вызывают переодическое изменения мгновенной мощности. Следовательно, мощность – величина переодически изменяющаяся, малоудобная для оценки энергетического состояния цепи, поэтому для этого основной величиной является средняя мощность. Эту мощность измеряет вольтметр. Обозначается – [p].

Для цепи синусоидального тока выразим через действующие значения напряжения и тока. Если в общ. случае напряжение на зажимах цепи опережает некоторый ток на угол φ, т.е.:

u=U_max(sinwt+φ), i=I_maxsinwt

то активная мощность будет равна:

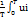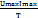p= dt = (cosφ 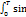²wtdt+sinwtcoswtdt)

Заменив sin²wt = (1-cos2wt)/2 и sinwtcoswt=sin2wt/2, получим:

p = 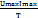( 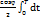- 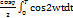+ sin )

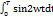2 и 3 интегралы в скобках = 0, т.к. это интеграл за целое число периодов.

Заменив Амплитуду через действующее значение получим основную формулу мощности

p=uicosφ

cosφ – коэффициент мощности. Чем меньше – тем хуже исполюзуется энергетическая установка.