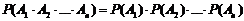Проверка гипотеза о зависимости (независимости) случайных величин

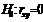
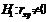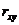Т.к. степень силы связи между случайными величинами, входящими в систему, определяется коэффициентом кореляции, то при определении независимости случайными величинами, входящими в систему, формируется гипотеза вида: Где - коэффициент кореляции между случайными величинами X или Y.

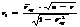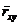В качестве выборочной функции при проверке этой гипотезы задаётся выражение вида: Где - статистический коэффициент кореляции.

При справедливости нулевой гипотезы данная выборочная функция имеет 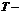распределение с числом степеней свободы 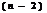, поэтому нулевая гипотеза проверяется по таблицам 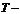распределения.

Если не подтверждается гипотеза о независимости случайных величин, то может быть сформулирована гипотеза о силе связи между случайными величинами, входящими в систему:

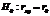
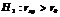
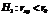
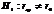
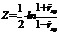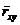Данная гипотеза проверяется по выборочной функции вида: где - статистический коэффициент корреляции.

Если справедлива нулевая гипотеза, то данная выборочная функция имеет стандартное нормальное распределение с характеристиками:

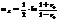
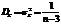
Чтобы нулевую гипотезу можно было проверить по таблицам нормального стандартного распределения, переходят к нормированным и центрированным выборочным функциям:

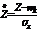(4)

Она имеет нормальное стандартное распределение. Поэтому нулевую гипотезу проверяют с помощью таблиц стандартного нормального распределения, т.е. по уровню значимости и виду альтернативной гипотезы определяют критическую область, а по выборочной функции (4) определяют её реализацию.

Если полученный результат попадает в критическую область, то нулевая гипотеза отклоняется.

1.Теория вероятностей изучает закономерности массовых случайных явлений.

Важным понятием в теории вероятностей является событие. Под событием понимается результат проведения опыта.

События бывают достоверные, невозможные и случайные. Достоверным называется событие, которое в результате опыта обязательно произойдёт. Невозможным называется событие, которое в результате опыта не произойдёт. Случайным называется событие, которое в результате опыта может как произойти, так и не произойти.

Вероятность события называют мерой случайной возможности. Вероятность достоверного события равна 1, вероятность невозможного события равна 0.

Классификация событий:

События 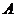и 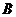называются несовместными, если появление одного из них исключает появление другого.

События 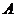и 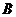называются совместными, если появление одного из них не исключает возможности появления другого события.

Событие 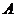называется благоприятствующим событию 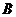, если появление события 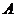влечёт за собой появление события .

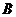События 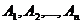образуют полную группу попарно несовместных событий, если в результате проведения опыта обязательно произойдёт одно и только одно из этих событий.

Событие 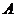и противоположное ему событи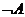е (не 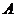) образуют полную группу несовместных событий.

В теории вероятностей первоначально существовало несколько подходов к понятию вероятности события.

Билет

Классическое определение вероятности событий: оно основывается на понятии равновозможности появления одного из n исходов при проведении опыта. Если в результате проведения опыта может произойти n исходов, а некоторому событию 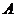благоприятствует 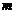исходов, то вероятность данного события определяется по формул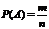е: где 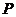– вероятность;( ) – записывается событие, ( 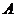) – рассматривается событие 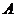; 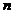– число возможных исходов; 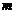– число благоприятных исходов.

Вероятность определяется ещё до опыта.

Статистическое определение вероятности: классическое определение вероятностей при переходе от простейших примеров к сложным становится неприменимым, так как во многих случаях не представляется возможным обосновать равновозможность всех исходов, которые могут произойти в результате проведения опыта. В этом случае вероятность события определяется по статистической схеме. Проводится n независимых опытов, определяется число опытов 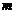, при которых появляется событие 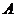, и статистическая вероятность определяется по формуле:

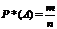
Геометрическая вероятность: с начала развития теории вероятностей были замечены недостатки как классического, так и статистического определения вероятности события. Это возникало в тех случаях, когда число возможных исходов при проведении опыта было равно бесконечности и число благоприятных исходов равнялось бесконечности. Поэтому было введено такое понятие как геометрическая вероятность.

Пусть множество М является возможными исходами. При этом данное множество является подмножеством либо числовой оси R (множество чисел), либо квадрата R² (плоскость), либо R³ (объём) и т.д.

Для решения вероятностей задачи вводится понятие меры некоторого события А: m(А) ("мю"). Под мерой события А может пониматься длина, площадь и т.д. Наряду с этой мерой вводится мера множества М - m(М). Тогда геометрическая вероятность события А определяется по формуле:

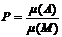
Для того чтобы все эти понятия объединить в единое понятие, Колмогоров разработал аксиоматическое построение теории вероятности.

Основные аксиомы теории вероятностей:

1. Каждому случайному событию А из поля событий F поставлено в соответствие неотрицательное число Р(А), называемое вероятностью события А.

2. Вероятность достоверного события равняется 1 (единице), а вероятность невозможного события равняется 0 (нулю).

3. Вероятность события А определяется в промежутке: 0 £ Р(А) £ 1.

4. Если события А₁, А₂, ..., А_n попарно несовместны, то вероятность суммы этих событий равна сумме вероятностей этих событий:

Р(А₁, А₂, ..., А_n) = Р(А₁) + Р(А₂) +...+ Р(А_n)

5. Если события А₁, А₂, ..., А_n представляют полную группу попарно несовместных событий, то вероятность суммы этих событий равна 1, то есть:

Из этой аксиомы следует:

Р(А) + Р(ØА) = 1 Р(А) = 1 – Р(ØА)

Билет

"О"Произведением двух событий А и В называется событие АВ, состоящее в том, что произойдёт и событие А, и событие В.

При рассмотрении вопроса произведения двух событий важным понятием является условная вероятность события.

"О" Вероятность события В называется условной, если она вычислена при условии, что событие А произошло, обозначается: Р(В/А).

"Т" Вероятность произведения двух событий равна произведению безусловной вероятности одного из событий на условную вероятность второго события, то есть вычисленную при условии, что первое событие произошло:

Р(АВ) = Р(А)×Р(В/А) = Р(В)×Р(А/В)

Доказательство: Докажем эту теорему по схеме равновозможных исходов. Пусть результат опыта сводится к появлению одного из n равнозначных исходов.

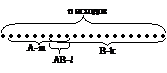Пусть некоторому событию А благоприятствует m исходов, а событию В – k исходов, обоим событиям благоприятствует l исходов. Так как все исходы равновозможны, то событие АВ по классической схеме равно отношению l к n, то есть: 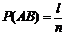(1)

Безусловная вероятность события А: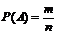(2)

Если произошло событие А, то вероятность того, что произойдёт один из l исходов, то есть что произойдёт событие В, будет равняться: 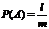(3)

Очевидно, что выражение (1) равно произведению выражений (2) и (3), то есть: 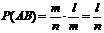что и требовалось доказать.Теорему о вероятности произведения двух событий можно распространить на вероятность произведения числа событий:

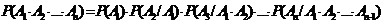Если события А₁, А₂, ..., А_n независимы, то вероятность произведения этих событий равна произведению их вероятностей: