Случайное событие. испытание. события достоверные и невозможные, совеместные и несовместные, полная группа событий, противоположные события.

СЛУЧАЙНОЕ СОБЫТИЕ. ИСПЫТАНИЕ. СОБЫТИЯ ДОСТОВЕРНЫЕ И НЕВОЗМОЖНЫЕ, СОВЕМЕСТНЫЕ И НЕСОВМЕСТНЫЕ, ПОЛНАЯ ГРУППА СОБЫТИЙ, ПРОТИВОПОЛОЖНЫЕ СОБЫТИЯ.

СС –явление, которое при одних и тех же условиях иногда происходит, иногда не происходит.

Испытание (опыт, эксперимент)–осуществление этих определенных условий.

Каждое испытание приводит к заранее точно не предсказуемому результату, т.е. его результат нельзя точно предсказать. И тем не менее СС является результатом испытания.

Достоверное событие (Ω), событие, которое обязательно происходит в результате испытания, вероятность достоверного события равна единице:Р(Ω)=1; невозможное событие (знак пустого множества), не происходит ни при каком исходе случайного эксперимента, вероятность невозможного события равна нулю.

Выпадение снега в НСК 30 ноября является случайным событием. Ежедневный восход Солнца можно считать достоверным событием. Выпадение снега в Африке можно рассматривать как невозможное событие.

События А и В назыв. совместными, если они могут произойти оба в результате одного опыта. В противном события называются несовместными.

Предположим, проводится подбрасывание монеты. В результате этого эксперимента обязательно произойдет одно из следующих событий:

А: монета упадет орлом;

В: монета упадет решкой;

С: монета упадет на ребро;

Т.е. система {А;В;С}является полной группой событий.

Противоположными называются два единственно возможных события, образующих полную группу. Если одно из событий, являющихся противоположными, обозначить через А, то противоположное событие обозначают через .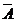

ПРОСТРАНСТВО ЭЛЕМЕНТАР. СОБ. ОПРЕДЕЛЕНИЕ СС. ОПЕРАЦИИ НАД СОБ. ОСНОВНЫЕ ОТНОШЕНИЯ МЕЖ СОБ.

Элементарным (ω) называется СС, которое не разделяется на другие, более мелкие события. Пространством элементарных событий (Ω) называется множество всех элементарных событий, связанных с данным испытанием.

1.При однократном подбрасывании монеты возможны два элементарных события: ω1=Г, ω2 = Ц, которые образуют пространство элементар. соб. Ω = {Г, Ц}.

2.Двукратное подбрасывание монеты: пространст­во элементарных событий определяется комбинацией элементарных событий при первом и втором подбра­сывании, то есть Ω = {ГГ, ГЦ, ЦГ, ЦЦ}.

В результате каждой операции над соб.получают новое событие.

Суммой (объединением) 2хсобытий А и В называется третье событие С, заключающееся в том, что произойдет хотя бы одно из них, то есть произойдет: 1) или только А, 2) или только В, 3) или оба вместе. Смысл суммы: событие А + В состоит из всех элементар. Соб., принадлежащих событию А или В.

Произведением (пересечением) двух событий А и В называется третье событие С, состоящее в совместном наступлении событий А и В. Обозначение произведе­ния событий: АВ = С. Смысл произведения заключается в том, что событие АВ состоит из элементарных событий, принадлежащих одновременно событию А и В.

Св-ва операций:

1.Переместительное. А+В=В+А и АВ=ВА.

2.Сочетательное А+В+С=(А+В)+С=А+(В+С)

АВС = (АВ)С=А(ВС)

3.Распределительное А(В+С)=АВ+АС

Отношение меж. Соб:

1.Отношение включения (А влечет за собой В). А явл. подмножеством В. Если происходит А, то и происходит В, но не наоборот.

2.Отношение несовместимости, т.е. соб А иВ вместе произойти не могут.

3. Отношение равносильности, т.е. соб А = соб В

СС –явление, которое при одних и тех же условиях иногда происходит, иногда не происходит.

ФОМУЛА БЕЙЕСА.

Вновь рассмотрим полную группу несовместных событий B1,B2..Bn, вероятности появления которых P(B1),P(B2)..P(Bn). Соб А может произойти только при условии наличия гипотез B1,B2..Bn Тогда по формуле полной вероятности Р(А)=Р(Н1)* Р(А|Н1) + Р(Н2)* Р(А|Н2)+…+ Р(Нк), *Р(А|Нк).

Если соб А произошло, то это может изменить вероятности гипотез P(B1),P(B2)..P(Bn).

По теореме умножения вероятностей

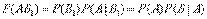
откуда

.

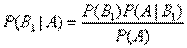Аналогично, для остальных гипотез

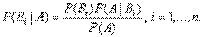
Полученная формула называется формулой Байеса.

Вероятности гипотез 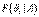называются апостериорными вероятностями (послеопытными), тогда как 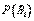- априорными вероятностями (доопытными).

ПР: Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго - 0,5; для третьего - 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.

Решение. Возможны три гипотезы:

А1 - на линию огня вызван первый стрелок,

А2 - на линию огня вызван второй стрелок,

А3 - на линию огня вызван третий стрелок.

Так как вызов на линию огня любого стрелка равновозможен, то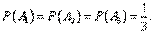

В результате опыта наблюдалось событие В - после произведенных выстрелов мишень не поражена. Условные вероятности этого события при сделанных гипотезах равны:

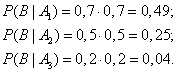
по формуле Байеса находим вероятность гипотезы А1 после опыта:

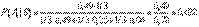
10. СХЕМА БЕРНУЛЛИ. ФОРМУЛА БЕРНУЛЛИ (док-во на примере). НАИВЕРОЯТНЕЙШЕЕ ЧИСЛО ПОЯВЛЕНИЙ СОБ В СХЕМЕ БЕРНУЛЛИ. ВЕРОЯТНОСТЬ НАСТУПЛЕНИЯ ХОТЯ БЫ 1ГО СОБ.

СЛУЧАЙНОЕ СОБЫТИЕ. ИСПЫТАНИЕ. СОБЫТИЯ ДОСТОВЕРНЫЕ И НЕВОЗМОЖНЫЕ, СОВЕМЕСТНЫЕ И НЕСОВМЕСТНЫЕ, ПОЛНАЯ ГРУППА СОБЫТИЙ, ПРОТИВОПОЛОЖНЫЕ СОБЫТИЯ.

СС –явление, которое при одних и тех же условиях иногда происходит, иногда не происходит.

Испытание (опыт, эксперимент)–осуществление этих определенных условий.

Каждое испытание приводит к заранее точно не предсказуемому результату, т.е. его результат нельзя точно предсказать. И тем не менее СС является результатом испытания.

Достоверное событие (Ω), событие, которое обязательно происходит в результате испытания, вероятность достоверного события равна единице:Р(Ω)=1; невозможное событие (знак пустого множества), не происходит ни при каком исходе случайного эксперимента, вероятность невозможного события равна нулю.

Выпадение снега в НСК 30 ноября является случайным событием. Ежедневный восход Солнца можно считать достоверным событием. Выпадение снега в Африке можно рассматривать как невозможное событие.

События А и В назыв. совместными, если они могут произойти оба в результате одного опыта. В противном события называются несовместными.

Предположим, проводится подбрасывание монеты. В результате этого эксперимента обязательно произойдет одно из следующих событий:

А: монета упадет орлом;

В: монета упадет решкой;

С: монета упадет на ребро;

Т.е. система {А;В;С}является полной группой событий.

Противоположными называются два единственно возможных события, образующих полную группу. Если одно из событий, являющихся противоположными, обозначить через А, то противоположное событие обозначают через 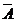.