Действие над события. Полная группа несовместных событий.

Основные понятия теории вероятностей. События и их виды.

Теория вероятностей - математическая наука, изучающая закономерности в случайных явлениях. Одним из основных понятий является понятие случайного события (в дальнейшем просто событие).

Событием называется всякий факт (исход), который в результате опыта (испытания, эксперимента) может произойти или не произойти. Каждому из таких событий можно поставить в соответствие определенное число, называемое его вероятностью и являющееся мерой возможного совершения этого события.

Множество – это любая совокупность объектов произвольной природы, каждый из которых называется элементом множества. События делятся на три категории:

Достоверное событие –это событие, которое обязательно произойдет в результате испытания.

Событие называется невозможным, если оно не происходит никогда в условиях данного эксперимента (испытания).

Случайное событие - может произойти или не произойти при выполнении определенной совокупности условий.

События называются равновозможными, если в результате испытаний ни одно из них не является более возможным, чем другое.

Совместные события– несколько событий называют совместными, если в результате эксперимента наступление одного из них не исключает появления других.

Несовместные события – несколько событий называют несовместными в данном эксперименте, если появление одного из них исключает появление других. Два события называются противоположными, если одно из них происходит тогда и только тогда, когда не происходит другое.

Событие, которое нельзя разбить на более простые, называется элементарным.

Событие, представимое в виде совокупности (суммы) нескольких элементарных событий, называется составным.

Вероятность события –это количественная мера, которая вводится для сравнения событий по степени возможности их появления.

События будут образовывать полную группу, если в результате испытаний появится хотя бы одно из них.

Частота события. Свойства частоты. Статистическое определение вероятности.

Пусть производится n опытов, в результате каждого из которых событие А происходит или нет.

Относительной частотой события А в данной серии испытаний называются отношение числа истыпаний, в которых А появилось, к общему числу испытаний: p*(A)= m\n.

Свойства частоты:

- Не отрицательное число (0<=p*(A)<=1)

- Частота достоверного события равна 1.

- Частота невозможного события равно 0.

- Частота суммы двух несовместимых событий равна сумме этих событий: p*(A+B)=p*(A)+p*(B).

Если А и В совместны, то можно подсчитать частоту А при условии, что В наступило – условная частота А.(р*(А|В).

- Частота произведения совместных событий равна произведению частоты одного из них на условную частоту другого: p*(AB)=p*(A)·p*(B|A)=p*(B)·p*(A|B)

Понятие частоты не универсально, т.к. частота меняется от опыта к опыту. Но при увеличении числа опытов, частота начинает принимать значения, мало отличающиеся от некоторого постоянного числа.

Относительная частота обладает статистической устойчивостью. Отсюда и статистическое определение вероятности – постоянное число, около которого группируются частоты случайного события по мере увеличения числа опытов.

Случайные величины, их виды. Законы распределения случайных величин.

Случайной величиной (СВ) называют величину, которая в результате наблюдения (испытания) принимает то или иное значение, заранее не известное и зависящее от случайных обстоятельств.

Функция Лапласа, её свойства. Правило «трех сигм»

Начальные и центральные моменты системы двух случайных величин. Необходимое условие независимости двух случайных величин системы.

Центральная предельная теорема. Различные формулировки.

Математическая статистика как наука. Основные понятия. Задачи математической статистики.

Математическая статистика – раздел математики, в котором изучаются методы сбора, систематизации и обработки результатов наблюдений массовых случайных явлений для выявления существующих закономерностей. Предметом математической статистики является изучение случайных величин (или случайных событий, процессов) по результатам наблюдений. Совокупность всех подлежащих изучению объектов или возможных результатов всех мыслимых наблюдений, производимых в неизменных условиях

над одним объектом, называется генеральной совокупностью.

Выборочной совокупностью (выборкой) называют совокупность объектов, отобранных случайным образом из генеральной совокупности. Более строго: выборка – это последовательность X1, X2, … Xn независимых одинаково распределенных случайных величин, распределение каждой из которых совпадает с распределением генеральной случайной величины.

Число объектов (наблюдений) в совокупности, генеральной или выборочной, называется ее объемом; обозначается соответственно через N и n.

Конкретные значения выборки, полученные в результате наблюдений (испытаний), называют реализацией выборки и обозначают строчными буквами x1, х2 …хn.

Метод статистического исследования, состоящий в том, что на основе изучения выборочной совокупности делается заключение о всей генеральной совокупности, называется выборочным.

Различают выборки с возвращением (повторные) и без возвращения (бесповторные). В первом случае отобранный объект возвращается в генеральную совокупность перед извлечением следующего; во втором – не возвращается. На практике чаще используется бесповторная выборка.

Выделим основные задачи математической статистики:

1. Задача определения закона распределения случайной величины (или системы случайных величин) по статистическим данным

2. Задача проверки правдоподобия гипотез

3. Задача нахождения неизвестных параметров распределения

Распределение Стьюдента.

Использование формул функций нормального распределения есть корректным , если аргумент выше указанных функций является беспрерывной величиной. Это означает, что расстояние между соседними измерениями есть бесконечно малыми и нуждается в бесконечном количестве наблюдений n. Для определения среднего квадратичного отклонения σмы должны решить уравнение: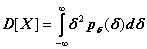

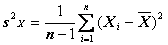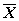В случае , если нам известные только количество n наблюдений и их величины x₁, ..xn , так называемая выборка , то по нее найти дисперсию D[X] мы не сможем. За выборкой мы сможем найти только точечную дисперсию , которую обозначим s²_X и определим ее как : где среднее арифметическое значение измеренной величины: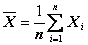

Переходя от точечной дисперсии отдельного наблюдения к точечной дисперсии среднего арифметического 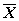с учетом количества наблюдений n имеем: ;

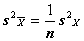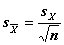
С учетом числа выборки n , получим = ;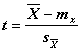

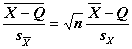Полученная случайная величина уже не будет иметь стандартное нормальное распределение!

Метод наименьших квадратов.

Метод моментов заключается в следующем: любой момент случайной величины 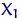(например, 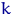-й) зависит, часто функционально, от параметра . Но тогда и параметр может оказаться функцией от теоретического 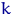-го момента. Подставив в эту функцию вместо неизвестного теоретического 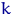-го момента его выборочный аналог, получим вместо параметра оценку 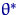. Пусть 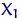, , 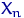— выборка объема 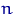из параметрического семейства распределений 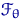, где 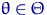. Выберем некоторую функцию 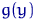так, чтобы существовал момент 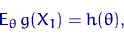и функция 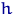была обратима в области . Тогда в качестве оценки 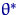для возьмем решение уравнения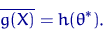

Или (что то же самое), сначала решаем уравнение относительно , а затем вместо истинного момента берем выборочный: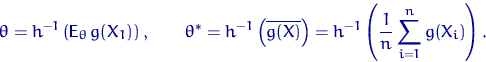

Чаще всего в качестве функции 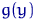берут 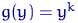. В этом случае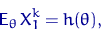

и, если функция 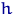обратима в области , то

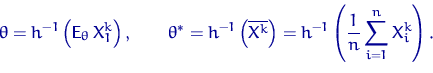
Можно сказать, что мы берем в качестве оценки такое (случайное) значение параметра , при котором истинный момент совпадает с выборочным.

Основные понятия теории вероятностей. События и их виды.

Теория вероятностей - математическая наука, изучающая закономерности в случайных явлениях. Одним из основных понятий является понятие случайного события (в дальнейшем просто событие).

Событием называется всякий факт (исход), который в результате опыта (испытания, эксперимента) может произойти или не произойти. Каждому из таких событий можно поставить в соответствие определенное число, называемое его вероятностью и являющееся мерой возможного совершения этого события.

Множество – это любая совокупность объектов произвольной природы, каждый из которых называется элементом множества. События делятся на три категории:

Достоверное событие –это событие, которое обязательно произойдет в результате испытания.

Событие называется невозможным, если оно не происходит никогда в условиях данного эксперимента (испытания).

Случайное событие - может произойти или не произойти при выполнении определенной совокупности условий.

События называются равновозможными, если в результате испытаний ни одно из них не является более возможным, чем другое.

Совместные события– несколько событий называют совместными, если в результате эксперимента наступление одного из них не исключает появления других.

Несовместные события – несколько событий называют несовместными в данном эксперименте, если появление одного из них исключает появление других. Два события называются противоположными, если одно из них происходит тогда и только тогда, когда не происходит другое.

Событие, которое нельзя разбить на более простые, называется элементарным.

Событие, представимое в виде совокупности (суммы) нескольких элементарных событий, называется составным.

Вероятность события –это количественная мера, которая вводится для сравнения событий по степени возможности их появления.

События будут образовывать полную группу, если в результате испытаний появится хотя бы одно из них.

Действие над события. Полная группа несовместных событий.

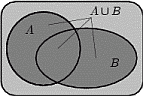
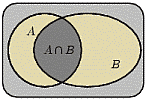
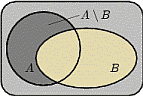
В теории вероятностей существуют ровно те же операции над множествами, что и в теории множеств. Геометрически события изображаются диаграммами Эйлера-Венна.

Объединением (сумма) 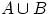событий 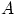и 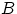называется событие, состоящее в том, что произошло либо 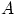, либо 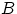, либо оба события одновременно. На языке теории множеств 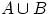есть множество, содержащее как элементарные исходы из множества 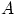, так и элементарные исходы из множества 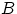. Пересечение(произведение) 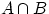событий 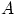и 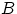называется событие, состоящее в том, что произошли оба события 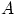и 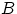одновременно. На языке теории множеств 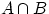есть множество, содержащее элементарные исходы, входящие в пересечение множеств 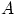и .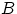

Дополнением (разность) 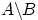события 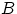до 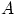называется событие, состоящее в том, что произошло событие 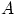, но не произошло 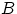. Т.е. множество 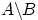содержит элементарные исходы, входящие в множество 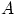, но не входящие в .

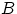Если 2 несовместных события образуют полную группу, то они будут противоположными.Противоположным (или дополнительным) к событию 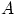называется событие 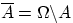, состоящее в том, что событие 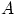в результате эксперимента не произошло. Т.е. множество 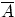состоит из элементарных исходов, не входящих в .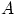