Неопределенный интеграл и определенный интегралы
281-290.Найти неопределенные интегралы. В пунктах а) и б) результаты проверить дифференцированием.
281.а) 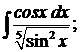

 б)
б) 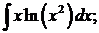
в) 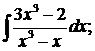 г)
г) 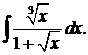
282. а) 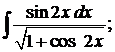 б)
б) 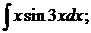
в) 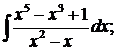 г)
г) 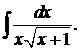
283. а) 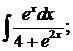 б)
б) 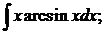
в) 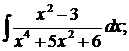 г)
г) 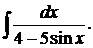
284.а) 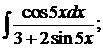 б)
б) 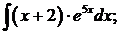
в) 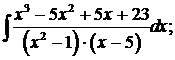 г)
г) 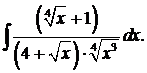
285.а)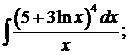 б
б 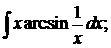
в) 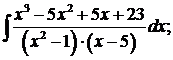 г)
г)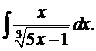
286.а) 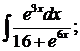 б)
б) 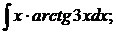
в) 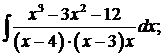 г)
г)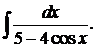
287.а) 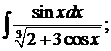 б)
б) 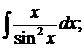
в) 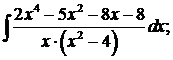 г)
г) 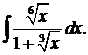
288. а) 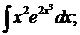 б)
б) 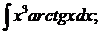
в) 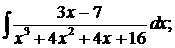 г)
г) 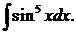
289. а) 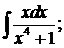 б)
б) 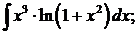
в) 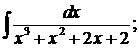 г)
г) 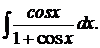
290. а) 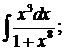 б)
б) 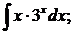
в) 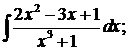 г)
г) 
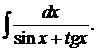
291-300. Вычислить приближенное значение определенного интеграла 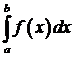 с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
291. 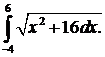 292.
292. 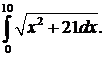
293. 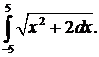 294.
294. 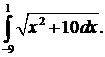
295. 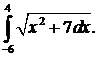 296.
296. 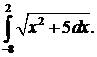
297. 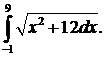 298.
298. 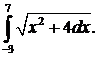
299. 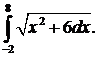 300.
300. 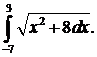
301-310.Вычислить несобственный интеграл или доказать его расходимость.
301. 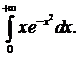 302.
302. 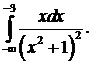
303. 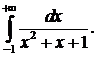 304.
304. 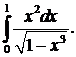
305. 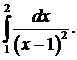 306.
306. 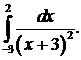
307. 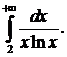 308.
308. 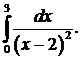
309. 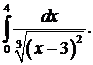 310.
310. 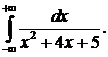
311.Вычислить площадь фигуры, ограниченной параболами 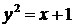 и
и 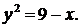
312. Вычислить площадь фигуры, ограниченной гиперболой 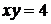 и прямой
и прямой 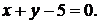
313.Вычислить площадь фигуры, ограниченной астроидой 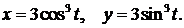
314. Вычислить площадь фигуры, ограниченной кардиоидой 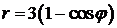 и окружностью
и окружностью 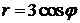 .
.
315. Вычислить объем тела, образованного вращением вокруг оси 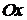 фигуры, ограниченной прямой
фигуры, ограниченной прямой 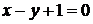 , другой косинусоиды
, другой косинусоиды 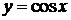 и осью
и осью 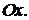
316. Вычислить объем тела, образованного вращением вокруг оси 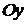 фигуры, ограниченной локоном Аньези
фигуры, ограниченной локоном Аньези 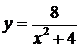 и параболой
и параболой 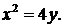
317.Вычислить объем тела, образованного вращением вокруг оси 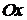 одной арки циклоиды
одной арки циклоиды 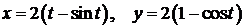 и осью
и осью 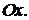
318. Вычислить длину дуги, параболы 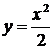 от начала координат до точки с абсциссой
от начала координат до точки с абсциссой 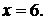
319.Вычислить длину одной арки циклоиды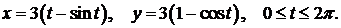
320.Вычислить длину первого витка архимедовой спирали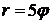 ,
, 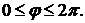
Дифференциальные уравнения
321-340.Найти общее решение дифференциального уравнения.
321. 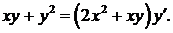 322.
322. 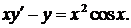
323. 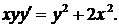 324.
324. 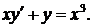
325. 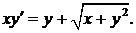 326.
326. 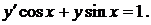
327 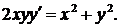 328
328 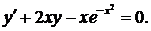
329. 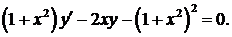 330.
330. 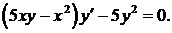
331. 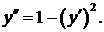 332.
332. 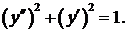
333. 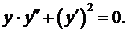 334.
334. 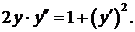
335. 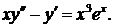 336.
336. 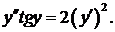
337. 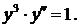 338.
338. 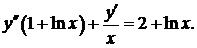
339. 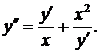 340.
340. 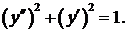
341-350.Найти частное решение дифференциального уравнения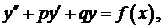 удовлетворяющее начальным условиям
удовлетворяющее начальным условиям 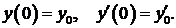
341. 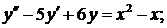
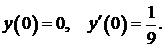
342. 
343. 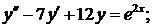
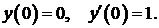
344. 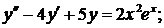
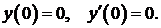
345. 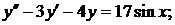
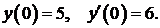
346. 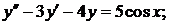
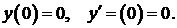
347. 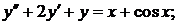
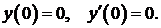
348. 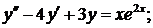
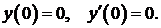
349. 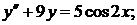
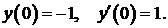
350. 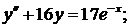
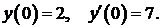
351-360.Дана система линейных дифференциальных уравнений с постоянными коэффициентами
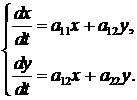
Требуется: 1) найти общее решение системы с помощью характеристического уравнения; 2) записать данную систему и ее решение в матричной форме.
351. 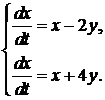
 352.
352. 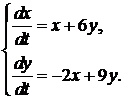
353. 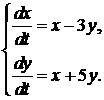 354.
354. 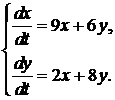
355. 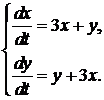 356.
356. 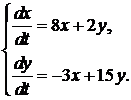
357. 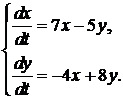 358.
358. 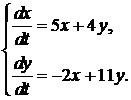
359. 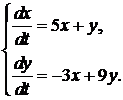 360.
360. 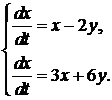
361.Найти кривую, у которой нормаль в любой ее точке равна расстоянию этой точки от начала координат.
362. Найти кривую, зная, что площадь, заключенная между осями координатной кривой и ординатой любой точки на ней, равна кубу этой ординаты.
363. Найти линию, для которой абсцисса центра тяжести криволинейной трапеции, образованной осями координат, прямой 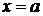 и линией, была равна
и линией, была равна 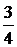 (при любом
(при любом  ).
).
364. Найти кривую, проходящую через точку 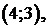 если угловой коэффициент касательной к кривой всегда в два раза меньше углового коэффициента радиуса – вектора точки касания.
если угловой коэффициент касательной к кривой всегда в два раза меньше углового коэффициента радиуса – вектора точки касания.
365. Найти кривую, у которой подкасательная равна среднему арифметическому координат точки касания.
366. Найти линию, у которой начальная ордината любой касательной равна соответствующей поднормали.
367. Тело движется прямолинейно с ускорением, пропорциональным произведению скорости движения 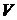 на время
на время 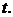 Установить зависимость между
Установить зависимость между 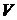 и
и 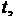 если
если 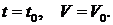
368. Моторная лодкадвижется в спокойной воде со скоростью 9км/ч. На полном ходу ее мотор был выключен, и через 20 сек скорость лодки уменьшилась до 4,5км/ч. Определить путь пройденный лодкой за 1 мин ( с момента выключения мотора).
369.Точка массой 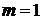 движется прямолинейно; на нее действует сила, пропорциональная времени, протекшему от момента, когда скорость равнялась нулю (коэффициент пропорциональности равен 2). Кроме того, точка испытывает сопротивление среды, пропорциональное скорости (коэффициент пропорциональности равен 3). Найти скорость в момент
движется прямолинейно; на нее действует сила, пропорциональная времени, протекшему от момента, когда скорость равнялась нулю (коэффициент пропорциональности равен 2). Кроме того, точка испытывает сопротивление среды, пропорциональное скорости (коэффициент пропорциональности равен 3). Найти скорость в момент 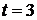 сек.
сек.
370.Материальная точка массой 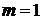 без
без 
 начальной скорости медленно погружается в жидкость. Найти путь, пройденной точкой за время
начальной скорости медленно погружается в жидкость. Найти путь, пройденной точкой за время 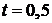 сек., считая, что при медленном погружении сила сопротивления жидкости пропорциональна скорости погружения (коэффициент пропорциональности равен 2).
сек., считая, что при медленном погружении сила сопротивления жидкости пропорциональна скорости погружения (коэффициент пропорциональности равен 2).
