Теорема 1. Неравенство Чебышева.
Закон больших чисел.
В широком смысле слова закон больших чисел означает, что при большом числе случайных экспериментов средний их результат практически перестает быть случайным и может быть предсказан с большой степенью определенности (т.е. событие имеет вероятность, близкую к 0 или 1).
В узком смысле под законом больших чисел в теории вероятности понимают ряд теорем, в которых устанавливается факт приближения различных характеристик большого числа опытов к некоторым постоянным (т.е. доказывается, что вероятность отклонения от них стремится к 1).
Теорема 1. Неравенство Чебышева.
Пусть X – cлучайная величина с заданными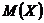 
и 
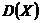. Тогда для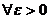 
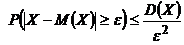. (1)
Неравенство оценивает вероятность того, что отклонение случайной величины X от центра распределения - 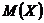превзойдет заданное определенное значение. Эта вероятность тем меньше, чем меньше .
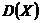Замечание.Оценка получается достаточно грубой, но зато это значение пригодно для любыхслучайных величин.
Пример 1.ПустьX – случайная величина, m = ,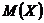 
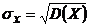. Используя неравенство Чебышева оценить 
.
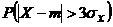Решение: Пусть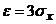 
, тогда 
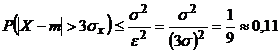. Но если случайная величина распределена по нормальному закону, то P=0,003 (правило «трех сигм»).
Определение:Говорят, что случайная величина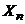 
сходится по вероятности к а, если при всех достаточно больших n выполняется неравенство:
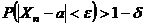или: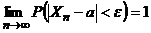 
,
где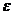 
- произвольное малое положительное число, а 
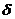зависит от выбора 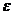и n.
Теорема 2. Теорема Чебышева.
Пусть X – cлучайная величина с заданным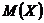и и 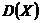. Тогда, при неограниченном увеличении количества независимых опытов, среднее арифметическое наблюдаемых значений случайной величины сходится по вероятности к ее математическому ожиданию, т.е.
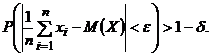(2)
В этом неравенстве можно принять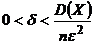 
, где 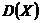- дисперсия случайной величины X.
Пример 2.Пусть в результате 100 независимых опытов найдены значения случайной величины X: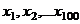 
. Пусть 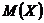=10, 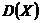=1. Оценить снизу вероятность того, что абсолютная величина разности между средним арифметическим наблюдаемых значений случайной величины 
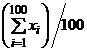и математическим ожиданием будет меньше 
.
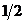Решение:
Воспользуемся неравенством (2):
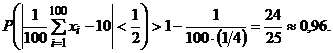
Таким образом, искомая вероятность больше 0,96.
Теорема Чебышева является одним из законов больших чисел, которые лежат в основе многих практических применений теории вероятностей.
Другим и притом простейшим (и ранее всех установленным) законом больших чисел является теорема Я. Бернулли.
Теорема 3. Теорема Бернулли.
Пусть проводится n независимых испытаний по схеме Бернулли, тогда, при неограниченном увеличении числа испытаний, частота случайного события сходится по вероятности к вероятности события, т.е.
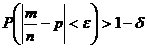, (3)
(причем можно принять, что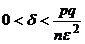 
), если вероятность события от испытания к испытанию не меняется и равна 
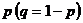, а m – число успехов в n испытаниях Бернулли.
Пример 3.
Монету подбрасывают 1000 раз. Оценить снизу вероятность отклонения частоты появления «герба» от вероятности его появления меньше, чем на 0,1.
Решение.
Здесь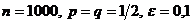 
. Используя неравенство (3), получим:
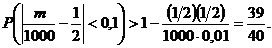
Неравенство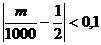 
равносильно двойному неравенству 400<m<600; поэтому можно сказать, что вероятность числа попаданий «герба» в интервал (400, 600) больше 
.
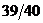Замечание. Теорема Чебышева говорит об устойчивости среднего арифметического наблюдаемых значений случайной величины, а теорема Бернулли (частный случай теорема Чебышева) выражает устойчивость частоты события (числа успехов в испытаниях Бернулли).
Пример 6.
Вероятность брака при производстве изделия равна 0,01. Изготовлено 1000 изделий. Найти вероятность того, что количество бракованных изделий а) лежит в пределах от 5 до 15; б) более 20; в) равно 10.
Решение.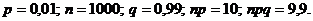 
Используем интегральную теорему М-Л:
а)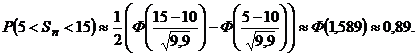 
б)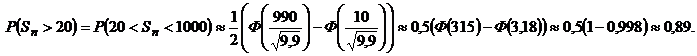 
в) Используем локальную теорему М-Л:
; 
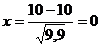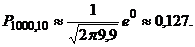
Здесь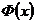 
- функция Лапласа.
-
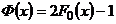формула связи функции Лапласа 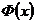и стандартной функции нормального распределения 
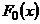. Функция Лапласа – четная, т.е.
.
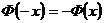Закон больших чисел.
В широком смысле слова закон больших чисел означает, что при большом числе случайных экспериментов средний их результат практически перестает быть случайным и может быть предсказан с большой степенью определенности (т.е. событие имеет вероятность, близкую к 0 или 1).
В узком смысле под законом больших чисел в теории вероятности понимают ряд теорем, в которых устанавливается факт приближения различных характеристик большого числа опытов к некоторым постоянным (т.е. доказывается, что вероятность отклонения от них стремится к 1).
Теорема 1. Неравенство Чебышева.
Пусть X – cлучайная величина с заданным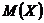и и 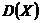. Тогда для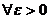
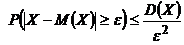. (1)
Неравенство оценивает вероятность того, что отклонение случайной величины X от центра распределения - 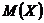превзойдет заданное определенное значение. Эта вероятность тем меньше, чем меньше .
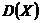Замечание.Оценка получается достаточно грубой, но зато это значение пригодно для любыхслучайных величин.
Пример 1.ПустьX – случайная величина, m = 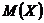, 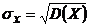. Используя неравенство Чебышева оценить .
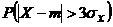Решение: Пусть 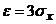, тогда 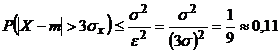. Но если случайная величина распределена по нормальному закону, то P=0,003 (правило «трех сигм»).
Определение:Говорят, что случайная величина 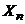сходится по вероятности к а, если при всех достаточно больших n выполняется неравенство:
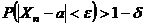или: ,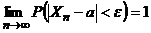
где 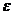- произвольное малое положительное число, а 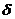зависит от выбора 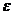и n.