Комбинаторика: сочетания, размещения, перестановки, правила суммы и произведения
В комбинаторике изучают вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).
Определение. Размещениями множества из 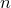 различных элементов по
различных элементов по 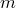 элементов
элементов 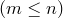 называются комбинации, которые составлены из данных
называются комбинации, которые составлены из данных 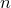 элементов по
элементов по 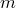 элементов и отличаются либо самими элементами, либо порядком элементов.
элементов и отличаются либо самими элементами, либо порядком элементов.
Число всех размещений множества из 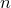 элементов по
элементов по 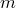 элементов обозначается через
элементов обозначается через 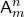 (от начальной буквы французского слова “arrangement”, что означает размещение), где
(от начальной буквы французского слова “arrangement”, что означает размещение), где 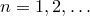 и
и 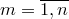 .
.
Теорема. Число размещений множества из 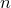 элементов по
элементов по 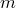 элементов равно
элементов равно
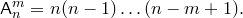
Определение. Перестановкой множества из 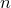 элементов называется расположение элементов в определенном порядке.
элементов называется расположение элементов в определенном порядке.
Так, все различные перестановки множества из трех элементов 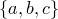 — это
— это
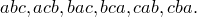
Очевидно, перестановки можно считать частным случаем размещений при 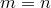 .
.
Число всех перестановок из 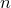 элементов обозначается
элементов обозначается 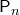 (от начальной буквы французского слова “permutation”, что значит “перестановка”, “перемещение”). Следовательно, число всех различных перестановок вычисляется по формуле
(от начальной буквы французского слова “permutation”, что значит “перестановка”, “перемещение”). Следовательно, число всех различных перестановок вычисляется по формуле
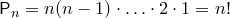
Определение. Сочетаниями из 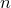 различных элементов по
различных элементов по 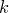 элементов называются комбинации, которые составлены из данных
элементов называются комбинации, которые составлены из данных 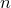 элементов по
элементов по 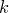 элементов и отличаются хотя бы одним элементом (иначе говоря,
элементов и отличаются хотя бы одним элементом (иначе говоря, 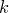 -элементные подмножества данного множества из
-элементные подмножества данного множества из 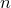 элементов).
элементов).
Как видим, в сочетаниях в отличие от размещений не учитывается порядок элементов. Число всех сочетаний из 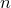 элементов по
элементов по 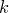 элементов в каждом обозначается
элементов в каждом обозначается 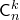 (от начальной буквы французского слова “combinasion”, что значит “сочетание”).
(от начальной буквы французского слова “combinasion”, что значит “сочетание”).
Числа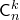
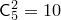


Случайные события, их классификация. Примеры.
Случайным называют событие, которое при осуществлении совокупности условий S может либо произойти, либо не произойти.
Различают события совместные и несовместные. События называются совместными, если наступление одного из них не исключает наступления другого. В противном случае события называются несовместными. Например, подбрасываются две игральные кости. Событие 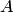 — выпадание трех очков на первой игральной кости, событие
— выпадание трех очков на первой игральной кости, событие 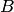 — выпадание трех очков на второй кости.
— выпадание трех очков на второй кости. 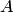 и
и 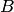 — совместные события. Пусть в магазин поступила партия обуви одного фасона и размера, но разного цвета. Событие
— совместные события. Пусть в магазин поступила партия обуви одного фасона и размера, но разного цвета. Событие 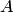 — наудачу взятая коробка окажется с обувью черного цвета, событие
— наудачу взятая коробка окажется с обувью черного цвета, событие 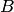 — коробка окажется с обувью ко
— коробка окажется с обувью ко
ричневого цвета, 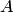 и
и 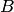 — несовместные события.
— несовместные события.
Событие называется достоверным, если оно обязательно произойдет в условиях данного опыта.
Событие называется невозможным, если оно не может произойти в условиях данного опыта. Например, событие, заключающееся в том, что из партии стандартных деталей будет взята стандартная деталь, является достоверным, а нестандартная — невозможным.
Событие называется возможным, или случайным, если в результате опыта оно может появиться, но может и не появиться. Примером случайного события может служить выявление дефектов изделия при контроле партии готовой продукции, несоответствие размера обрабатываемого изделия заданному, отказ одного из звеньев автоматизированной системы управления.
События называются равновозможными, если по условиям испытания ни одно из этих событий не является объективно более возможным, чем другие. Например, пусть магазину поставляют электролампочки (причем в равных количествах) несколько заводов-изготовителей. События, состоящие в покупке лампочки любого из этих заводов, равновозможны.
Важным понятием является полная группа событий. Несколько событий в данном опыте образуют полную группу, если в результате опыта обязательно появится хотя бы одно из них. Например, в урне находится десять шаров, из них шесть шаров красных, четыре белых, причем пять шаров имеют номера. 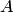 — появление красного шара при одном извлечении,
— появление красного шара при одном извлечении, 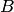 — появление белого шара,
— появление белого шара, 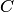 — появление шара с номером. События
— появление шара с номером. События 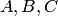 образуют полную группу совместных событий.
образуют полную группу совместных событий.
Введем понятие противоположного, или дополнительного, события. Под противоположным событием 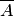 понимается событие, которое обязательно должно произойти, если не наступило некоторое событие
понимается событие, которое обязательно должно произойти, если не наступило некоторое событие 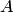 . Противоположные события несовместны и единственно возможны. Они образуют полную группу событий. Например, если партия изготовленных изделий состоит из годных и бракованных, то при извлечении одного изделия оно может оказаться либо годным — событие
. Противоположные события несовместны и единственно возможны. Они образуют полную группу событий. Например, если партия изготовленных изделий состоит из годных и бракованных, то при извлечении одного изделия оно может оказаться либо годным — событие 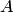 , либо бракованным — событие
, либо бракованным — событие 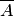 .
.
20.Вероятность случайного события. Классическое определение вероятности. Свойства вероятности.
