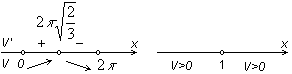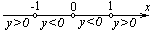Геометрические задачи на нахождение оптимальных значений величин.
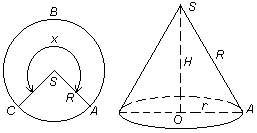
Задание. Из кружка жести радиуса Rвырезается сектор и из оставшейся части круга делается коническая воронка. При какой величине угла вырезаемого сектора объём воронки будет наибольшим?
| № шага | План решения | Применение плана | |
| Строим рабочий чертеж | ||
| Записываем исходную формулу для вычисления величины, экстремальное значение которой требуется найти | 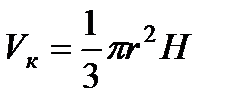 | ||
| Вводим переменную величину х и выражаем через неё значения всех величин исходной формулы | Пусть х – величина центрального угла оставшегося сектора, тогда 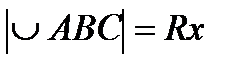 и и 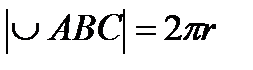 , значит , значит 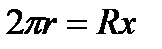 и и 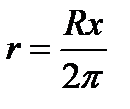 . Высота воронки . Высота воронки 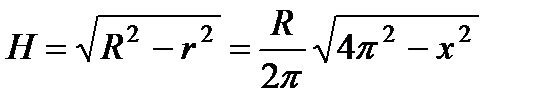 | ||
| Подставляя найденные значения величин в формулу, представляем её как функцию аргумента х | 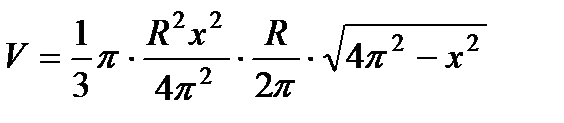 , , 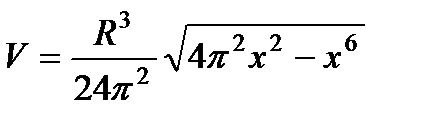 | ||
| Задаем (по смыслу задачи) область определения функции | 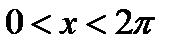 , , 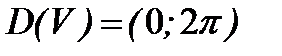 | ||
| Функцию аргумента х исследуем на экстремум на найденном числовом промежутке | 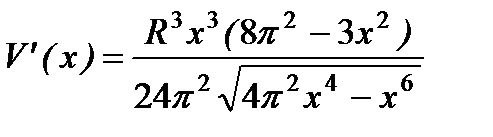 , , 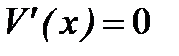 , , 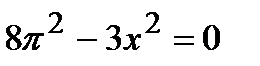 , , 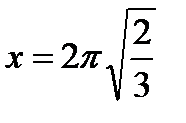 , , 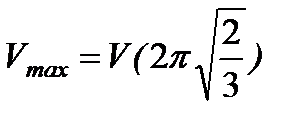 | |
| Записываем ответ | Величина вырезаемого угла равна 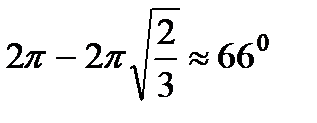 |
ВАРИАНТЫ ПРАКТИЧЕСКОЙ РАБОТЫ.
Вариант 1.
1. Найдите наибольшее и наименьшее значения функции 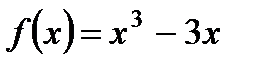 на отрезке
на отрезке 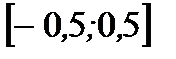 .
.
2. Из квадратного листа жести со стороной 12 м надо изготовить бак с квадратным основанием без крышки наибольшего объема. Найдите размеры бака и его объем.
Вариант 2.
1. Найдите наибольшее и наименьшее значения функции 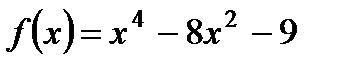 на отрезке
на отрезке 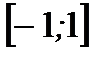 .
.
2. Какой из прямоугольников с периметром 2pимеет наибольшую площадь?
Вариант 3.
1. Найдите наибольшее и наименьшее значения функции 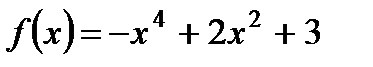 на отрезке
на отрезке 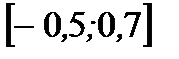 .
.
2. Разность двух чисел равна 8. Каковы должны быть эти числа. Чтобы произведение куба первого числа на второе было наименьшим?
Вариант 4.
1. Найдите наибольшее и наименьшее значения функции 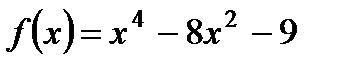 на отрезке
на отрезке 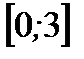 .
.
2. Для стоянки машин выделили площадку прямоугольной формы, примыкающую одной стороной к стене здания. Площадку обнесли с трех сторон металлической сеткой длиной 200 м. И площадь ее при этом оказалась наибольшей. Каковы размеры площадки?
Вариант 5.
1. Найдите наибольшее и наименьшее значения функции 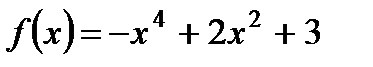 на отрезке
на отрезке 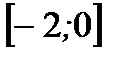 .
.
2. Из куска картона 32 см 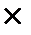 20 см требуется изготовить открытую сверху коробку наибольшей вместимости, вырезая по углам квадраты и затем, загибая выступы для образования боковых сторон коробки. Найдите объем коробки.
20 см требуется изготовить открытую сверху коробку наибольшей вместимости, вырезая по углам квадраты и затем, загибая выступы для образования боковых сторон коробки. Найдите объем коробки.
Вариант 6.
1. Найдите наибольшее и наименьшее значения функции 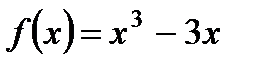 на отрезке
на отрезке 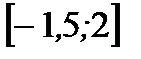 .
.
2. Требуется сделать коробку, объем которой должен равняться 108 см 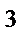 . Коробка открыта сверху и имеет квадратное дно. Каковы должны быть ее размеры, чтобы на ее изготовление пошло наименьшее количество материала?
. Коробка открыта сверху и имеет квадратное дно. Каковы должны быть ее размеры, чтобы на ее изготовление пошло наименьшее количество материала?
Вариант 7.
1. Найдите наибольшее и наименьшее значения функции 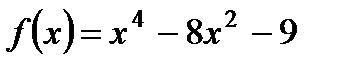 на отрезке
на отрезке 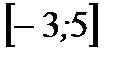 .
.
2. На странице книги печатный текст должен занимать (вместе с промежутками между строк)
160 см 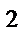 . Ширина полей на странице слева и справа должна быть равна 2 см, а сверху и снизу – 5 см. Если принимать во внимание только экономию бумаги, то каковы должны быть наиболее выгодные размеры страницы?
. Ширина полей на странице слева и справа должна быть равна 2 см, а сверху и снизу – 5 см. Если принимать во внимание только экономию бумаги, то каковы должны быть наиболее выгодные размеры страницы?
Вариант 8.
1. Найдите наибольшее и наименьшее значения функции 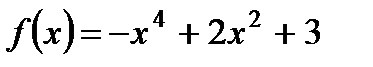 на отрезке
на отрезке 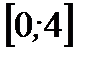 .
.
2. Материальная точка совершает прямолинейное движение по закону 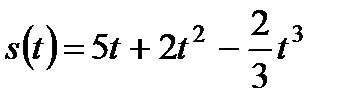 , где t – время в секундах, s – путь в метрах. В какой момент времени t скорость движения точки будет наибольшей и какова величина этой наибольшей скорости?
, где t – время в секундах, s – путь в метрах. В какой момент времени t скорость движения точки будет наибольшей и какова величина этой наибольшей скорости?
ПРАКТИЧЕСКАЯ РАБОТА №5
«Свойства функций»
ЦЕЛЬ РАБОТЫ:
1. Корректировать знания, умения и навыки в теме: «Свойства функций».
2. Закрепить и систематизировать знания по теме.
3. Определить уровень усвоения знаний, оценить результат деятельности уч-ся.
ОБОРУДОВАНИЕ: микрокалькуляторы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1. Ответить на контрольные вопросы:
а) Что называется функцией?
б) Что такое естественная область определения функции?
в) Какая функция называется четной, нечетной?
г) Как найти точки пересечения графика функции с осями координат?
ВАРИАНТЫ ПРАКТИЧЕСКОЙ РАБОТЫ
Вариант 1.
1. Найдите 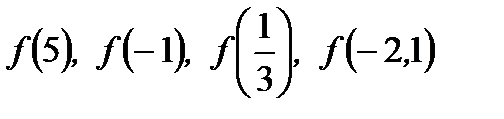 , если
, если 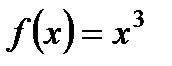 .
.
2. Найдите область определения функции 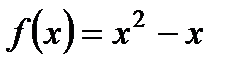 .
.
3. Установите, является ли функция 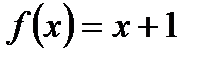 четной, нечетной или не является ни четной, ни нечетной.
четной, нечетной или не является ни четной, ни нечетной.
4. Найдите точки пересечения графика функции 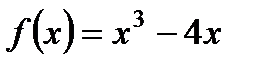 с осью ОУ и нули функции.
с осью ОУ и нули функции.
Вариант 2.
1. Найдите 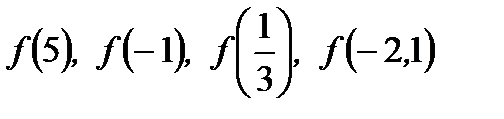 , если
, если 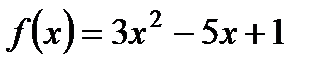 .
.
2. Найдите область определения функции 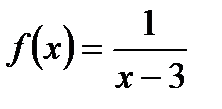 .
.
3. Установите, является ли функция 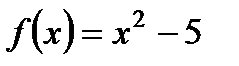 четной, нечетной или не является ни четной, ни нечетной.
четной, нечетной или не является ни четной, ни нечетной.
4. Найдите точки пересечения графика функции 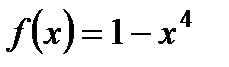 с осью ОУ и нули функции.
с осью ОУ и нули функции.
Вариант 3.
1. Найдите 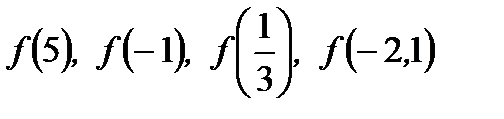 , если
, если 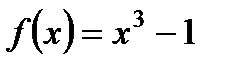 .
.
2. Найдите область определения функции 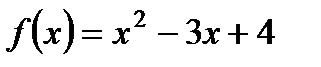 .
.
3. Установите, является ли функция 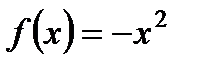 четной, нечетной или не является ни четной, ни нечетной.
четной, нечетной или не является ни четной, ни нечетной.
4. Найдите точки пересечения графика функции 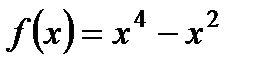 с осью ОУ и нули функции.
с осью ОУ и нули функции.
Вариант 4.
1. Найдите 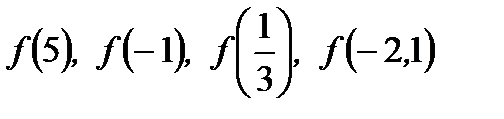 , если
, если 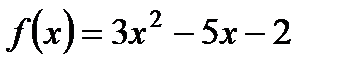 .
.
2. Найдите область определения функции 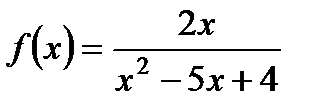 .
.
3. Установите, является ли функция 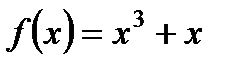 четной, нечетной или не является ни четной, ни нечетной.
четной, нечетной или не является ни четной, ни нечетной.
4. Найдите точки пересечения графика функции 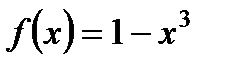 с осью ОУ и нули функции.
с осью ОУ и нули функции.
Вариант 5.
1. Найдите 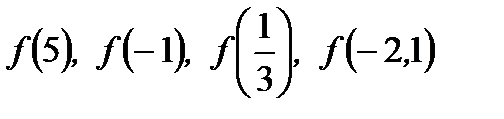 , если
, если 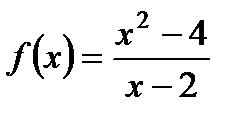 .
.
2. Найдите область определения функции 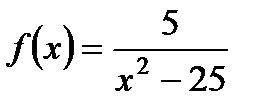 .
.
3. Установите, является ли функция 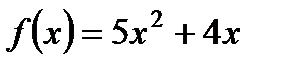 четной, нечетной или не является ни четной, ни нечетной.
четной, нечетной или не является ни четной, ни нечетной.
4. Найдите точки пересечения графика функции 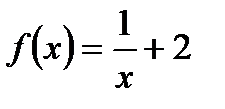 с осью ОУ и нули функции.
с осью ОУ и нули функции.
Вариант 6.
1. Найдите 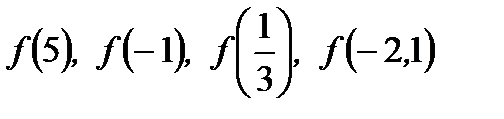 , если
, если 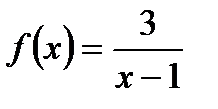 .
.
2. Найдите область определения функции 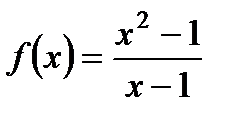 .
.
3. Установите, является ли функция 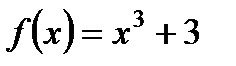 четной, нечетной или не является ни четной, ни нечетной.
четной, нечетной или не является ни четной, ни нечетной.
4. Найдите точки пересечения графика функции 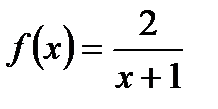 с осью ОУ и нули функции.
с осью ОУ и нули функции.
Вариант 7.
1. Найдите 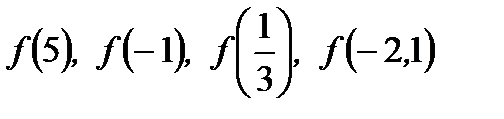 , если
, если 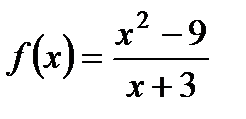 .
.
2. Найдите область определения функции 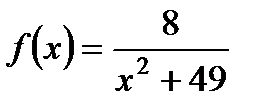 .
.
3. Установите, является ли функция 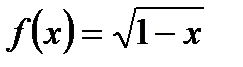 четной, нечетной или не является ни четной, ни нечетной.
четной, нечетной или не является ни четной, ни нечетной.
4. Найдите точки пересечения графика функции 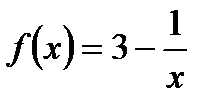 с осью ОУ и нули функции.
с осью ОУ и нули функции.
Вариант 8.
1. Найдите 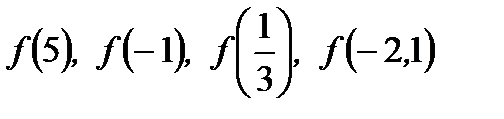 , если
, если 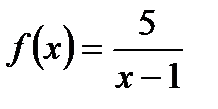 .
.
2. Найдите область определения функции 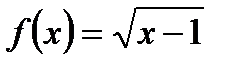 .
.
3. Установите, является ли функция 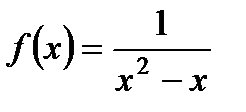 четной, нечетной или не является ни четной, ни нечетной.
четной, нечетной или не является ни четной, ни нечетной.
4. Найдите точки пересечения графика функции 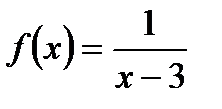 с осью ОУ и нули функции.
с осью ОУ и нули функции.
ПРАКТИЧЕСКАЯ РАБОТА №6
«Исследование функции и построение ее графика»
ЦЕЛЬ РАБОТЫ:
1. Корректировать знания, умения и навыки в теме: «Исследование функции и построение ее графика».
2. Закрепить и систематизировать знания по теме.
3. Определить уровень усвоения знаний, оценить результат деятельности уч-ся.
ОБОРУДОВАНИЕ: таблицы производных элементарных функций, микрокалькуляторы.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
1. Ответить на контрольные вопросы:
а) Какую точку называют критической (стационарной) точкой функции?
б) Сформулируйте признак возрастания (убывания) функции.
в) Сформулируйте признак максимума (минимума) функции.
г) Опишите схему исследования функции.
2. С помощью обучающей таблицы повторить план исследования функции и изучить образцы решенных примеров.
3. Выполнить задания для самоконтроля (в таблице).
ОБУЧАЮЩАЯ ТАБЛИЦА
Задание. Исследуйте и постройте графики функции:
а) 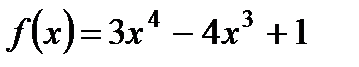 ;б)
;б) 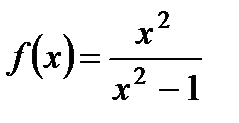 .
.
| № | План исследования | Применение | плана | ||
| шага | Функции | а)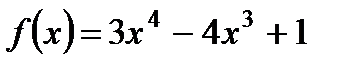 | б) 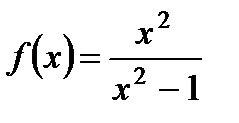 | ||
| Находим область определения функции | 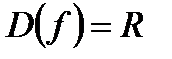 | 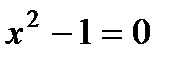 , , 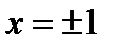 , , 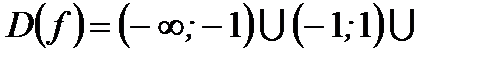 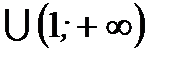 | |||
| Исследуем функцию на четность, нечетность | 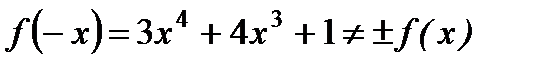 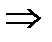 функция ни четная, ни нечетная функция ни четная, ни нечетная | 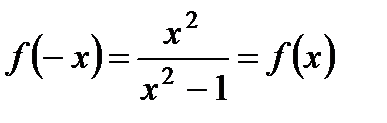 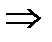 функция четная функция четная | |||
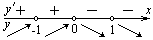
| Находим нули (корни) функции и промежутки её знакопостоянства | 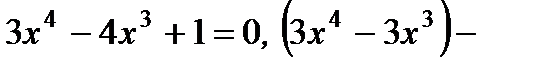 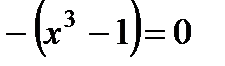 , , 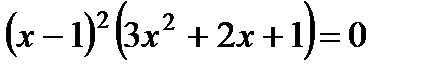 , , 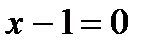 , , 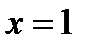 - нуль функции - нуль функции | 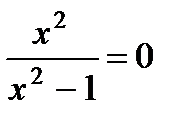 , , 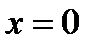 - нуль функции - нуль функции | ||
| Находим производную функции и её критические точки | 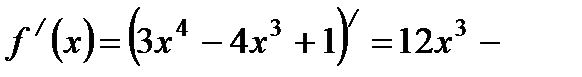 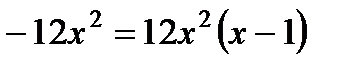 , , 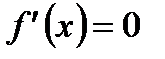 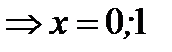 - критические точки функции - критические точки функции | 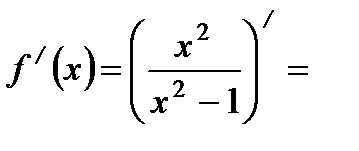 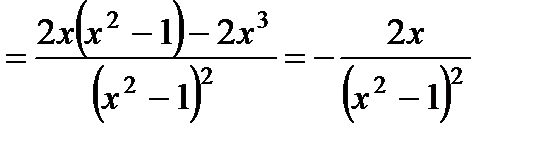 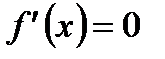 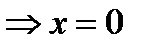 - критическая точка функции - критическая точка функции | |||
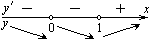
| Находим промежутки монотонности, точки экстремума и экстремумы функции | 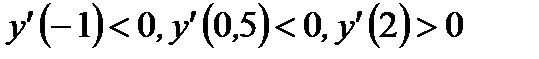 х=0 – не является точкой экстремума, х=1 – точка минимума, х=0 – не является точкой экстремума, х=1 – точка минимума, 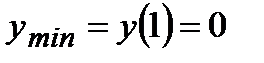 | 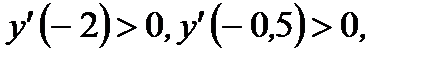 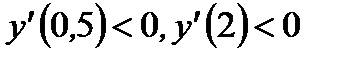 , х=0 – точка максимума, , х=0 – точка максимума, 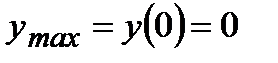 | ||
Находим предел функции при 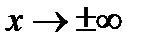 | 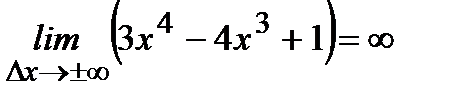 | 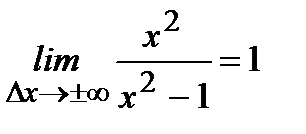 | |||
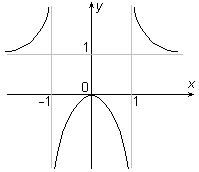
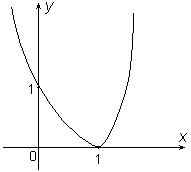
| Строим эскиз графика функции |
Примеры. Исследуйте и постройте графики функций:
1) 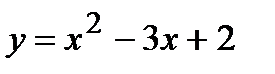 ; 2)
; 2) 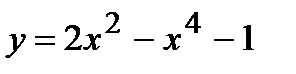 ; 3)
; 3) 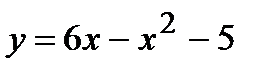 ; 4)
; 4) 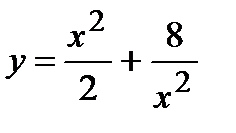 ; 5)
; 5) 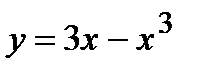 ; 6)
; 6) 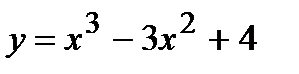 ; 7)
; 7) 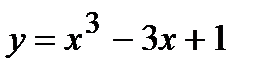 ; 8)
; 8) 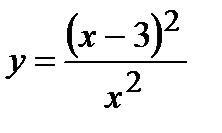 ; 9)
; 9) 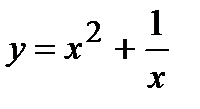 .
.
ВАРИАНТЫ ПРАКТИЧЕСКОЙ РАБОТЫ.
Вариант 1.
1. Исследуйте функцию 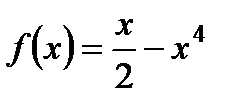 на максимум и минимум.
на максимум и минимум.
2. Исследуйте с помощью производной функцию 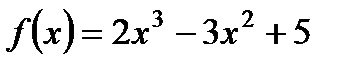 и постройте ее график.
и постройте ее график.
Вариант 2.
1. Исследуйте функцию 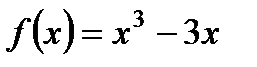 на максимум и минимум.
на максимум и минимум.
2. Исследуйте с помощью производной функцию 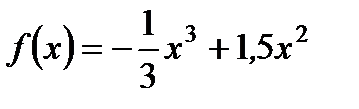 и постройте ее график.
и постройте ее график.
Вариант 3.
1. Исследуйте функцию 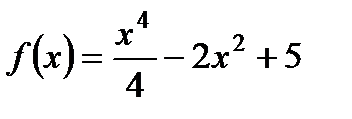 на максимум и минимум.
на максимум и минимум.
2. Исследуйте с помощью производной функцию 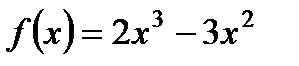 и постройте ее график.
и постройте ее график.
Вариант 4.
1. Исследуйте функцию 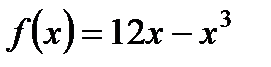 на максимум и минимум.
на максимум и минимум.
2. Исследуйте с помощью производной функцию 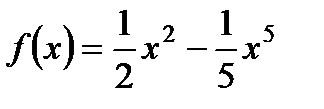 и постройте ее график.
и постройте ее график.
Вариант 5.
1. Исследуйте функцию 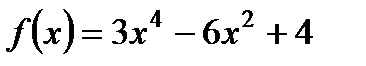 на максимум и минимум.
на максимум и минимум.
2. Исследуйте с помощью производной функцию 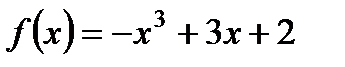 и постройте ее график.
и постройте ее график.
Вариант 6.
1. Исследуйте функцию 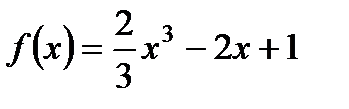 на максимум и минимум.
на максимум и минимум.
2. Исследуйте с помощью производной функцию 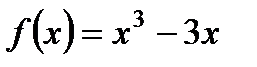 и постройте ее график.
и постройте ее график.
Вариант 7.
1. Исследуйте функцию 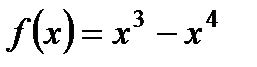 на максимум и минимум.
на максимум и минимум.
2. Исследуйте с помощью производной функцию 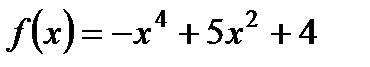 и постройте ее график.
и постройте ее график.
Вариант 8.
1. Исследуйте функцию 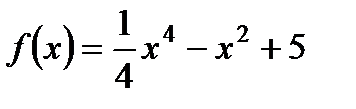 на максимум и минимум.
на максимум и минимум.
2. Исследуйте с помощью производной функцию 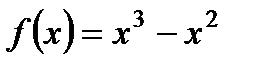 и постройте ее график.
и постройте ее график.
ПРАКТИЧЕСКАЯ РАБОТА №7