Нахождение длины отрезка и координат середины отрезка

Пусть А и В — произвольные точки плоскости с координатами А (х_1; y₁;z₁) и В (х₂; у₂;z₂) соответственно. Тогда длина отрезка :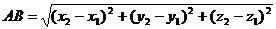

Пусть М(х;у;z) середина отрезка АВ. Тогда верны формулы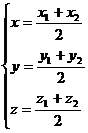

Векторы и координаты

Величины, которые характеризуются не только численным значением, но и направлением, называют векторами. Геометрически векторы изображаются направленными отрезками. Вектор характеризуется следующими элементами: начальной точкой, направлением, длиной.

Если начало вектора есть А, а его конец В, то вектор обозначается символом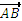

Ненулевые векторы называются коллинеарными, если они, либо лежат на одной прямой, либо на параллельных прямых. Обозначаются коллинеарные векторы так: .

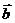Длина вектора – это длина отрезка, изображающего вектор.

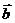Если два ненулевых вектора и коллинеарны и имеют одно направление – то они называются сонаправленными, если противоположное – то противоположно направленными.

Векторы называются равными, если они сонаправлены и их длины равны, т.е.

1) ↑↑

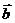
2)

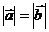
Сложение векторов

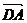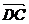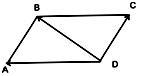
Если два вектора и выходят из одной точки, то их суммой будет вектор 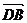совпадающий с диагональю параллелограмма, построенного на этих векторах , и выходящей из этой же точки(правило параллелограмма) + =

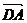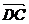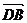
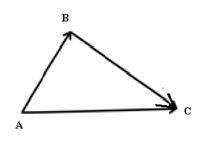
Если один вектор выходит из конца другого, то суммой будет вектор, соединяющий начало одного с концом другого (правило треугольника).

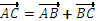
Если два вектора 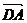и 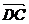выходят из одной точки, то разностью их будет вектор 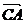совпадающий с диагональю параллелограмма, построенного на этих векторах, и выходящей из конца второго вектора в начало первого - =

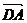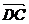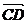
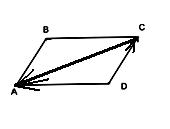
Произведением вектора на число 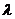называется вектор, обозначаемый 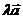, длина которого равна 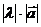и который сонаправлен с вектором , если 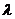>0 и противоположно направлен с ним, если 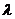<0.

ТЕОРЕМА Если точка М- середина отрезка АВ, то для любой точки Р верно равенство = ( + )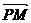

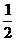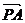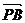ТЕОРЕМА. Два ненулевых вектора и 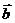коллинеарны тогда и только тогда, когда существует число 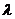, такое что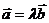

Векторы называются компланарными, если они лежат в одной или в параллельных плоскостях.

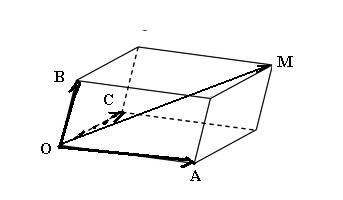
Для сложения трех некомпланарных векторов справедливо правило параллелепипеда: если три вектора 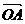, , 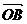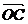отложены от одной точки и построен параллелепипед для которого отрезки OA,OB,OC- являются ребрами, то диагональ ОМ этого параллелепипеда изображает сумму векторов 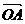, , 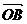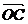.То есть + + =

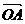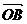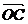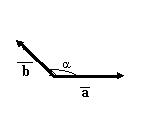
Угол между векторами

Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором.

Координаты вектора

Если точка А имеет координаты (х₁; у₁;z₁), а точка В имеет координаты (х₂; у₂;z₂),

то координаты вектора 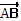это числа (x₂-x₁); (y₂-y₁); (z₂-z₁).

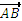
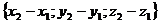, то есть чтобы найти координаты вектора надо из координат конца вектора вычесть соответственно координаты начала вектора.

В этом случае длина вектора выражается через его координаты следующим образом:

=

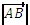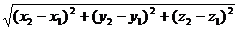
При сложении векторов складываются их координаты.

При умножении вектора на число k, на это число умножается каждая из его координат.

Если два вектора равны, то соответственно равны их координаты.