Координаты середины отрезка

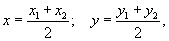11. Вектор – направленный отрезок. Другими словами, вектором называется отрезок, для которого указано, какой из его концов является началом, а какой концом.

На рисунках направление вектора обозначается стрелкой от начала к концу. Если длина рассматриваемого отрезка равна нулю, то есть отрезок вырождается в точку, то эта точка тоже может рассматриваться как вектор. Такой вектор называется нулевым и имеет произвольное направление.

Длиной (модулем) ненулевого вектора 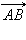называется длина отрезка AB. Она обозначается как 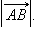Длина нулевого вектора равна нулю: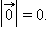

Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.

Поскольку нулевой вектор может иметь произвольное направление, то разумно считать его коллинеарным любому ненулевому вектору.

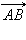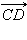Если два ненулевых вектора и коллинеарны, а лучи AB и CD сонаправлены, то векторы 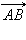и 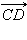называются сонаправленными. Этот факт обозначается так: 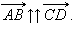Если же эти лучи не являются сонаправленными, то векторы 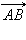и 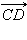называются противонаправленными. Этот факт обозначается так: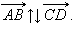

Два вектора называются равными, если они сонаправлены и их длины равны.

От любой точки пространства можно отложить вектор, равный данному, и притом только один.

Два вектора называются противоположными, если их длины равны, и они противоположно направлены

Суммой двух векторов 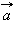и 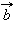называется новый вектор 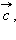который обозначается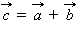

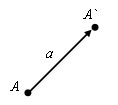
Есть вектора a. Пусть A (x; y) – начло вектора, а A` (x`; y`) – конец вектора. Координатами вектора a называются числа a1=x-x`, a2=y-y`. Для обозначения того, что вектор a имеет координаты a1 и a2, используют запись a (a1; a2) или (a1; a2).

Абсолютная величина вектора a (a1; a2) равна

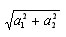
Если начало вектора совпадает с его концом, то это нулевой вектор, обозначается (0).

12. Модулем (длиной) вектора 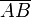называется длина(норма) соответствующего вектора 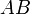и обозначается как .

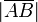Модулем вектора A называется длинна вектора, она равна по абсолютной величине квадратному корню из суммы квадратов компонент вектора. Любой вектор характеризуется направлением, которое задается одним или более углов между выбранными осями координат (ортами) и модулем этого вектора.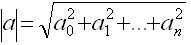

Два вектора называются равными, если они совмещаются параллельным переносом.
Т.е. существует такой параллельный перенос, при котором начало и конец одного вектора совмещается с началом и концом другого вектора соответственно.

Теорема

Если векторы одинаково направлены и равны по абсолютной величине, то они равны.

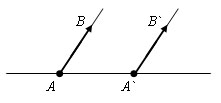
Доказательство.

Пусть AB и CD – одинаково направленные векторы, равные по абсолютной величине. Параллельный перенос, переводящий точку A` в точку A, совмещает луч A`B` с лучом AB, потому что они сонаправлены. Отрезка AB и A`B` равны, поэтому точка B совмещается с точкой B`. Значит, параллельный перенос переводит вектор A`B` в вектор AB. Значит векторы равны. Теорема доказана.

Суммой векторов а(а1;а2;а3) и b(b1;b2;b3) называется вектор с(а1+b1;а2+b2;а3+b3)

Произведением вектора а(а1;а2;а3)на число λназывается вектор λа=(λа1; λа2; λа3)

13. Угол между векторами — угол между направлениями этих векторов (наименьший угол).

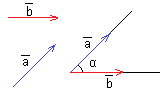
По определению, угол между двумя векторами находится в промежутке [0°; 180°].
Угол между векторами 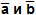обозначается так: .
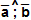Если векторы перпендикулярны, то угол между ними равен 90º. Если векторы сонаправлены, в частности один из них или оба нулевые, то угол между ними равен 0^о. Если противоположно направленные векторы, то угол между ними равен 180º.
Угол между двумя ненулевыми векторами находится с помощью вычисления скалярного произведения. По определению скалярное произведение равно произведению длин векторов на косинус угла между ними (скалярное произведение для двух векторов с координатами (x₁; y₁) и (x₂; y₂) вычисляется по формуле: x₁x₂ + y₁y₂).

Скалярным произведением векторов(а1;а2;а3) и (b1;b2;b3) называется число а1b1+а2b2+а3b3.

14. Два ненулевых (не равных 0) вектора называются коллинеа́рными, если они лежат на параллельных прямых или на одной прямой. Допусти́м синоним — «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или противоположно направлен. Коллинеарные векторы: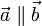

Разложение по двум неколлинеарным векторам

Пусть 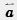и 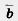— отличные от нуля неколлинеарные векторы. Докажем, что любой вектор с можно представить в виде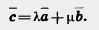

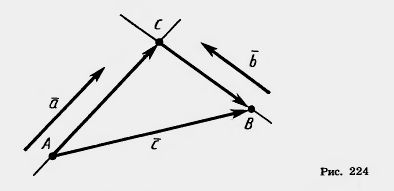
Пусть А и В — начало и конец вектора 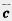(рис. 224). Проведем через точки А и В прямые, параллельные векторам 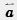и 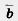. Они пересекутся в некоторой точке С. Имеем: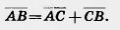

Так как векторы 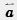и 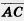коллинеарны, то 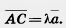. Так как векторы 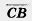и 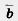коллинеарны, то 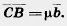. Таким образом, 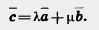что и требовалось доказать.

15. Компланарные векторы

Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости. Любые два вектора компланарны.

Три вектора, среди которых имеются два коллинеарных, также компланарны.

Три произвольных вектора могут быть компланарными (лежать в одной плоскости) или некомпланарными (не лежать в одной плоскости).

КОМПЛАНАРНЫЕ ВЕКТОРЫ

- векторы, параллельные одной плоскости. Необходимым и достаточным условием компланарности трех векторов

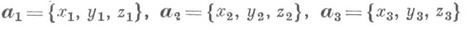
является равенство:

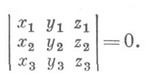
Разложение по трем некомпланарным векторам

Любой вектор m может быть представлен, и притом единственным образом, в виде линейной комбинации трех любых некомпланарных векторов а, b и с:

m = xa + yb + zc.

Прежде всего отметим, что никакие два вектора из векторов а, b, с не коллинеарны; в противном случае векторы а, b, с были бы компланарны. Поэтому, если вектор m компланарен с какими-нибудь двумя векторами (например, с а и b), то m = ха + уb и, следовательно,

m = ха + уb + 0 • с,

т. е. в этом случае теорема доказана.