Линейные однородные дифференциальные уравнения n-го порядка с постоянными коэффициентами
Число: 2085
Вид уравнения: 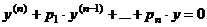 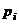 - числа - числа | Характер корней характеристического уравнения | |||
Корни действительные, различные, т. е. 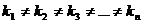 | Корни действительные, есть повторяющиеся, т.е. 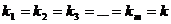 (корень кратности m) (корень кратности m) | Корни комплексные, различные 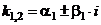 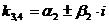 и т. д. и т. д. | Корни комплексные, есть повторяющиеся 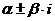 - пара корней кратности - пара корней кратности 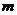 | |
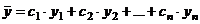 - общее решение денного уравнения, где - общее решение денного уравнения, где 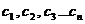 - произвольные постоянные, - произвольные постоянные, 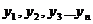 - фундаментальная система решений данного уравнения. - фундаментальная система решений данного уравнения. | Вид частных решений 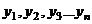 , соответствующих корням характеристического уравнения , соответствующих корням характеристического уравнения | |||
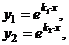  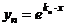 | 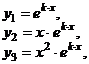 , , 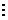 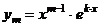 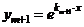 . . . . . . . . . . . . . . . . . . . . . . . . | 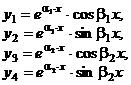 . . . . . . . . . . . . . . . . . . . . . . . . | 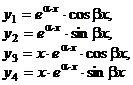 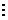 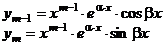 | |
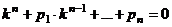 - характеристическое уравнение - характеристическое уравнение |
22. Линейные неоднородные дифференциальные уравнения n-го порядка
с постоянными коэффициентами
Вид уравнения: 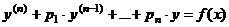 | Метод вариации произвольных постоянных | Метод подбора частного решения | |
Если 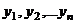 - фундаментальная система решений соответствующего однородного уравнения, то общее решение неоднородного уравнения находится по формуле - фундаментальная система решений соответствующего однородного уравнения, то общее решение неоднородного уравнения находится по формуле 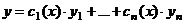 , если , если 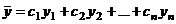 где где 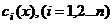 находится из системы уравнений находится из системы уравнений 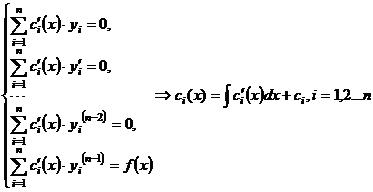 Частный случай: Частный случай: 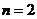 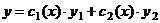 , , 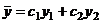 где где 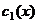 и и 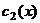 находятся из системы уравнений находятся из системы уравнений 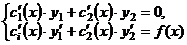 Þ найти Þ найти 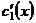 и и 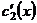 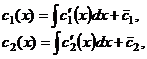 где где 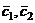 - постоянные - постоянные | 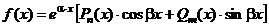 - специальный вид правой части неоднородного уравнения (пусть - специальный вид правой части неоднородного уравнения (пусть 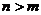 ) Частное решение ) Частное решение 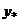 ищется в виде ищется в виде 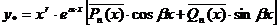 , где , где 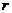 – кратность корней – кратность корней 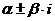 характеристического уравнения: характеристического уравнения: 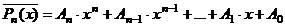 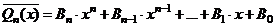 То есть То есть 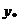 зависит от правой части зависит от правой части 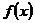 и от корней характеристического уравнения. и от корней характеристического уравнения. | ||
Структура общего решения: 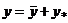 , где , где 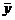 - общее решение соответствующего однородного уравнения, - общее решение соответствующего однородного уравнения, 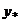 - частное решение неоднородного уравнения. - частное решение неоднородного уравнения. | |||
Если 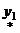 - частное решение уравнения - частное решение уравнения 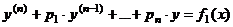 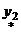 - частное решение уравнения - частное решение уравнения 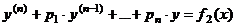 , то , то 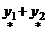 - частное решение уравнения - частное решение уравнения 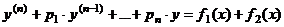 |
Числовые ряды. Основные понятия
| № п/п | Понятие | Определение и обозначение | ||
| 1. | Ряд | 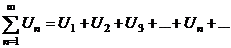 | ||
| 2. | Члены ряда, общий ( n – ый ) член ряда | 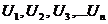 - бесконечная числовая последовательность, где - бесконечная числовая последовательность, где 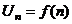 | ||
| 3. | Частичные суммы ряда | 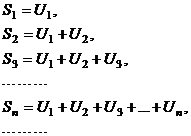 | ||
| 4. | Последовательность частичных сумм | 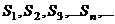 | ||
| 5. | Сходящиеся ряды | 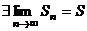 , где , где 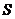 – сумма ряда – сумма ряда 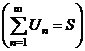 | ||
| 6. | Расходящиеся ряды | 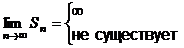 | ||
| 7. | Остаток ряда | 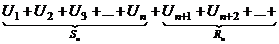 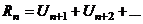 | ||
| Основные свойства сходящихся рядов | ||||
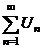 сходится сходится |  | 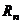 - сходится - сходится | ||
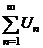 сходится, сходится, 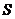 – его сумма – его сумма |  | 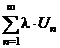 сходится, сходится, 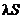 - его сумма - его сумма | ||
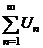 сходится, сходится, 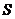 – его сумма – его сумма |  | 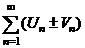 - сходится и - сходится и | ||
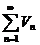 сходится, сходится, 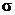 – его сумма – его сумма | 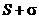 - его сумма - его сумма | |||
| Необходимый признак сходимости ряда | ||||
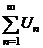 - сходится - сходится |  | 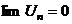 | ||
Следствие: 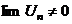 |  | 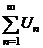 - расходится - расходится | ||
Числовые ряды с положительными членами
Определение 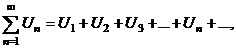 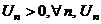 - действительные числа - действительные числа | ||||||||
| Некоторые ряды и их поведение | Гармонический ряд 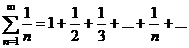 расходится расходится | |||||||
Обобщенный гармонический ряд 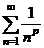 при при 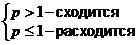 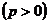 | ||||||||
| Ряд геометрический | 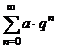 при при 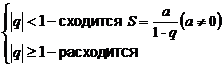 | |||||||
В частности при 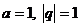 ряды ряды | 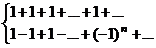 расходится расходится | |||||||
| Достаточные признаки сходимости числовых рядов с положительными членами | ||||||||
| Признаки сравнения | Интегральный признак Коши | Признак Даламбера | Признак Коши | |||||
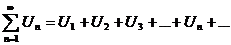 (1) (1) 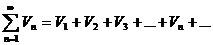 (2) (2) | 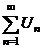 , , 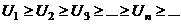 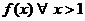 : непрерывная, положительная, невозрастающая : непрерывная, положительная, невозрастающая 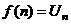 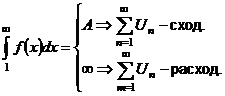 Замечание: Замечание: 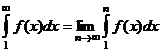 | 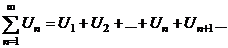 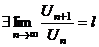 | 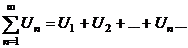 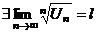 | |||||
1. 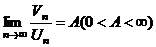 где где 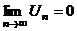 , , 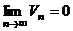 (при (при 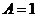 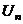 ~ ~ 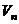 ) ) | Þ | 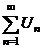 и и 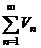 одновременно сходятся или расходятся одновременно сходятся или расходятся | а) 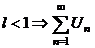 - сход. б) - сход. б) 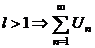 - расход. - расход. | а) 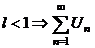 - сход. б) - сход. б) 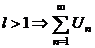 - расход. - расход. | ||||
2. а) 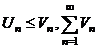 сход. сход. | Þ | 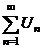 сход сход | Замечание: 1. Если 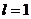 , то признак Даламбера и Коши не дают ответа о поведении ряда. 2. Признак Даламбера иногда используется без предельного перехода: , то признак Даламбера и Коши не дают ответа о поведении ряда. 2. Признак Даламбера иногда используется без предельного перехода: 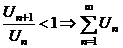 сход., сход., 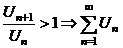 расход. расход. | |||||
б) 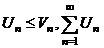 расход. расход. | Þ | 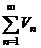 расход. расход. | ||||||
Замечание: В качестве рядов для сравнения удобно выбирать ряды 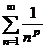 и и 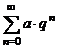 | ||||||||
