Понятие производной, ее геометрический и физический смысл
Определение 1. Производной (первой производной) функции 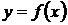 называется предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю, если этот предел существует и конечен.
называется предел отношения приращения функции к приращению аргумента при стремлении приращения аргумента к нулю, если этот предел существует и конечен.
Если 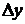 считать приращением функции
считать приращением функции 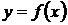 , соответствующим приращению аргумента
, соответствующим приращению аргумента 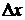 , то имеет место равенство
, то имеет место равенство 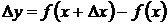 . В соответствии с определением производной
. В соответствии с определением производной
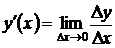 ,
,
здесь 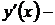 обозначение производной (первой производной), позднее будут введены другие обозначения производных.
обозначение производной (первой производной), позднее будут введены другие обозначения производных.
Определение 2. Функция 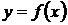 называется дифференцируемой в точке представлено в виде
называется дифференцируемой в точке представлено в виде 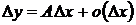 , причем
, причем 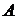 не зависит от
не зависит от 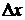 , а
, а 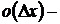 бесконечно малая при
бесконечно малая при 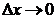 более высокого порядка малости по сравнению с
более высокого порядка малости по сравнению с 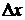 , то есть
, то есть 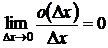 .
.
Рассмотрим, чему равняется 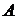 , для чего поделим полученное равенство на
, для чего поделим полученное равенство на 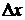 и перейдем к пределу при
и перейдем к пределу при 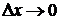 . Очевидно
. Очевидно
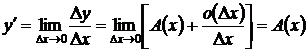 .
.
Итак,
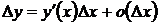 .
.
Поскольку 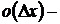 бесконечно малая более высокого порядка малости, чем
бесконечно малая более высокого порядка малости, чем 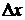 , при малых значениях
, при малых значениях 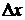 второе слагаемое правой части формулы для приращения значительно меньше по сравнению с первым, то есть при малых значениях
второе слагаемое правой части формулы для приращения значительно меньше по сравнению с первым, то есть при малых значениях 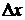 приближенно можно считать
приближенно можно считать
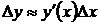 , или
, или 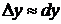 , где
, где 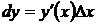 - дифференциал функции.
- дифференциал функции.
Таким образом, дифференциал функции является основной частью ее приращения. Для удобства записи дифференциала функции вводят обозначение 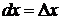 , тогда
, тогда 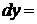 , что позволяет ввести еще одно обозначение производной
, что позволяет ввести еще одно обозначение производной 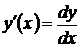 .
.
Геометрический смысл производной
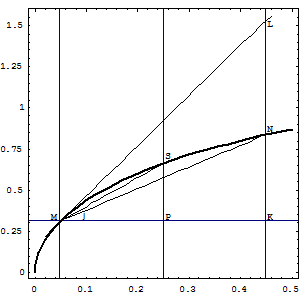
Рисунок 34.
Возьмем две точки кривой  :
: 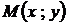 и
и 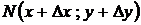 , соединим их хордой (смотри рисунок). Пусть
, соединим их хордой (смотри рисунок). Пусть 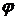 - угол между хордой
- угол между хордой 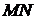 и осью
и осью 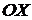 , тогда
, тогда 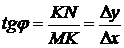 . Уменьшим
. Уменьшим 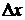 вдвое, при этом точка
вдвое, при этом точка 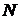 , смещаясь вдоль кривой, займет положение
, смещаясь вдоль кривой, займет положение 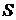 . Обозначим угол между хордой
. Обозначим угол между хордой 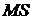 и осью абсцисс
и осью абсцисс 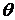 . Для рассматриваемого случая
. Для рассматриваемого случая 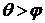 , что видно из рисунка. Если далее уменьшать приращение аргумента
, что видно из рисунка. Если далее уменьшать приращение аргумента 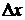 , точка
, точка 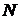 еще более приближается к точке
еще более приближается к точке 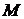 , изменяется угол хорды, соединяющей точки, с осью
, изменяется угол хорды, соединяющей точки, с осью 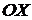 . Ясно, что при
. Ясно, что при 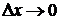 точки
точки 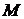 и
и 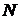 в конечном итоге сливаются, хорда становится касательной к кривой
в конечном итоге сливаются, хорда становится касательной к кривой 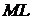 , а угол наклона хорды становится углом
, а угол наклона хорды становится углом 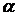 касательной к кривой с осью
касательной к кривой с осью 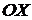 . Таким образом, из
. Таким образом, из 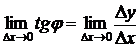 следует
следует 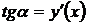 .
.
Итак, геометрический смысл производной функции в заданной точке – это тангенс угла между касательной к кривой в указанной точке и осью абсцисс.
Физический (механический) смысл производной
Из школьного курса физики известно, что средняя скорость движения равна отношению пройденного пути ко времени его прохождения то есть
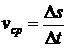 , где
, где 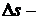 пройденный путь,
пройденный путь, 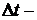 время его прохождения. Известно также, что средняя скорость практически не дает информации о движении объекта. В самом деле, если человек, желающий сесть в поезд на станции, находящейся посредине между начальным и конечным пунктами движения, знает, что поезд проходит весь путь, скажем за 16 часов, то он придет на станцию через восемь часов после начала движения поезда из начального пункта и на поезд может опоздать. Дело в том, что поезд практически никогда не идет со средней скоростью. На станциях его скорость равна нулю, затем он набирает скорость, некоторое время идет с постоянной скоростью, затем начинает скорость уменьшать при подходе к очередной станции и так далее. Если на первом участке пути скорость поезда выше, чем на втором, и остановок меньше, то, первую половину пути он пройдет быстрее, чем вторую. Знание средней скорости поезда нашего пассажира подведет. Какая же скорость дает полную информацию о движении объекта? Это мгновенная скорость движения, или скорость в данный момент времени. Именно она равняется нулю во время пребывания поезда на станциях, она возрастает при отходе его со станций, она же уменьшается при подходе к станциям. Как подсчитать мгновенную скорость движения? Математика дает ответ на этот вопрос. Нужно подсчитать предел средней скорости при
время его прохождения. Известно также, что средняя скорость практически не дает информации о движении объекта. В самом деле, если человек, желающий сесть в поезд на станции, находящейся посредине между начальным и конечным пунктами движения, знает, что поезд проходит весь путь, скажем за 16 часов, то он придет на станцию через восемь часов после начала движения поезда из начального пункта и на поезд может опоздать. Дело в том, что поезд практически никогда не идет со средней скоростью. На станциях его скорость равна нулю, затем он набирает скорость, некоторое время идет с постоянной скоростью, затем начинает скорость уменьшать при подходе к очередной станции и так далее. Если на первом участке пути скорость поезда выше, чем на втором, и остановок меньше, то, первую половину пути он пройдет быстрее, чем вторую. Знание средней скорости поезда нашего пассажира подведет. Какая же скорость дает полную информацию о движении объекта? Это мгновенная скорость движения, или скорость в данный момент времени. Именно она равняется нулю во время пребывания поезда на станциях, она возрастает при отходе его со станций, она же уменьшается при подходе к станциям. Как подсчитать мгновенную скорость движения? Математика дает ответ на этот вопрос. Нужно подсчитать предел средней скорости при 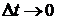 . Итак,
. Итак,
 .
.
Следовательно, скорость движения в каждый момент времени равна производной от пути по времени. В этом заключается физический смысл производной. Если абстрагироваться от реального движения, то можно утверждать, что физический смысл производной – это скорость изменения функции.
Теорема. Дифференцируемая на некотором интервале функция непрерывна в нем.
Доказательство. Поскольку функция 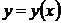 дифференцируема на некотором интервале, ее производная, а следовательно,
дифференцируема на некотором интервале, ее производная, а следовательно, 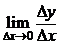 имеет во всех его точках конечное значение, но это возможно только при
имеет во всех его точках конечное значение, но это возможно только при 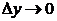 , в противном случае
, в противном случае 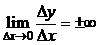 . Таким образом,
. Таким образом, 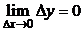 , что совпадает с одним из определений непрерывности функции.
, что совпадает с одним из определений непрерывности функции.
Правила дифференцирования
1. Производная суммы двух функций равна сумме производных этих функций, то есть
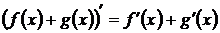 .
.
Доказательство. Пусть 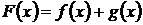 , тогда
, тогда
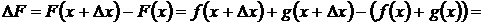
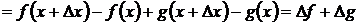
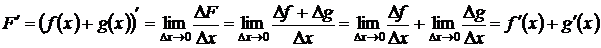
2. Производная произведения: 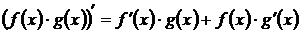 .
.
Доказательство. Пусть 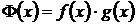 , тогда
, тогда
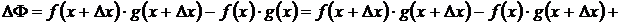
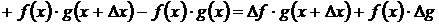 ,
,
откуда следует
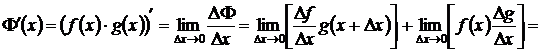
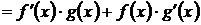 .
.
При получении этой формулы используются два свойства пределов: предел произведения равен произведению пределов, и предел функции 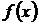 , не зависящей от
, не зависящей от 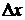 , равен самой функции.
, равен самой функции.
3. Производная частного двух функций:
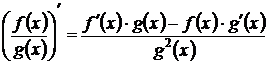 .
.
Формула приводится без доказательства (с ним можно познакомиться в одном из рекомендованных учебников).
4. Производная сложной функции. Пусть 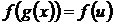 , где
, где 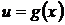 , тогда
, тогда
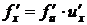 ,
,
здесь 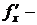 есть искомая производная функции
есть искомая производная функции 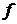 по переменной
по переменной 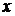 , а
, а 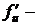 производная этой же функции по промежуточному аргументу
производная этой же функции по промежуточному аргументу 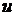 .
.
Доказательство.
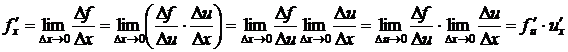 .
.
При доказательстве формулы использовался переход от вычисления предела при 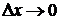 к пределу при
к пределу при 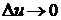 . Этот переход законен, если
. Этот переход законен, если 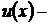 непрерывная функция, что следует из третьего определения непрерывности функции.
непрерывная функция, что следует из третьего определения непрерывности функции.
Следствие. Это свойство можно обобщить и на большее количество промежуточных аргументов функции. Рассмотрим, например, функцию 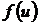 , где
, где 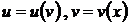 . Очевидно, промежуточных аргументов здесь два
. Очевидно, промежуточных аргументов здесь два 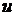 и
и 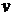 , тогда
, тогда 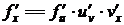 и так далее.
и так далее.
5. Производная обратной функции. Рассмотрим функцию 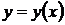 и обратную ей
и обратную ей 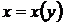 . Установим связь между производными этих функций.
. Установим связь между производными этих функций.
 .
.
В доказательстве формулы использовался переход от вычисления предела при 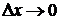 к пределу при
к пределу при 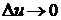 , что, как говорилось выше, является законным для непрерывных функций.
, что, как говорилось выше, является законным для непрерывных функций.
Для дальнейшей работы с производными необходима таблица производных элементарных функций.
Таблица производных
1. 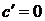 , если
, если 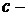 постоянная.
постоянная.
Доказательство. Поскольку 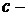 постоянная, ее приращение равно нулю, то есть
постоянная, ее приращение равно нулю, то есть 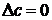 . Очевидно,
. Очевидно, 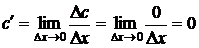 .
.
2. 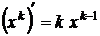 для любых
для любых 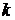 .
.
Докажем это свойство для 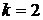 . Пусть
. Пусть 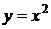 , тогда
, тогда
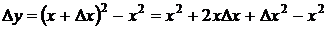 ,
,
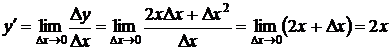 .
.
Для других 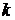 доказательство будет приведено позднее.
доказательство будет приведено позднее.
3. 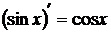 .
.
Доказательство: 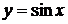 ,
,
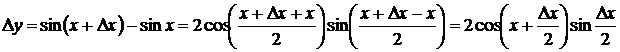
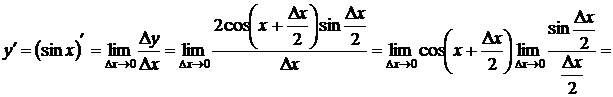
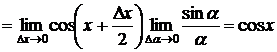 .
.
При вычислении второго из пределов сделана замена переменной 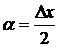 , затем использован первый замечательный предел.
, затем использован первый замечательный предел.
4. 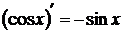 (доказывается аналогично).
(доказывается аналогично).
5. 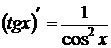 .
.
Доказательство:
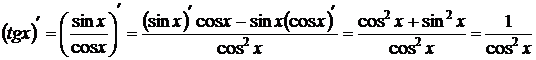 .
.
6. 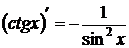 . Доказательство аналогично.
. Доказательство аналогично.
7. 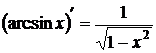 .
.
Доказательство:
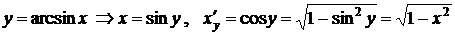 , откуда имеем
, откуда имеем
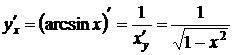 .
.
8. 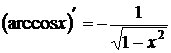 . Доказывается аналогично.
. Доказывается аналогично.
9. 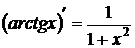 .
.
Доказательство:
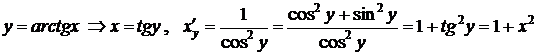 ,
,
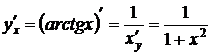 .
.
10. 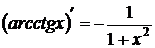 .
.
11. 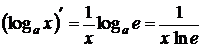 .
.
Доказательство. Пусть 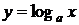 , тогда
, тогда
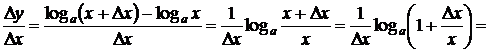
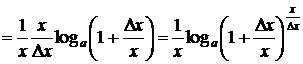 ,
,
откуда следует
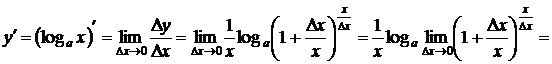
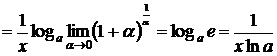 .
.
В ходе доказательства использовались следующие свойства логарифмов:
а) 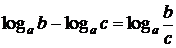 , б)
, б) 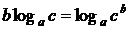 , в)
, в) 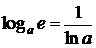 ,
,
также использовалась замена переменной 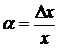 , после чего – второй замечательный предел. Постоянная
, после чего – второй замечательный предел. Постоянная 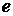 и натуральный логарифм
и натуральный логарифм 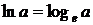 были введены при рассмотрении второго и третьего замечательных пределов. Поскольку логарифм – функция непрерывная, перестановка местами логарифма и предела следует из первого определения непрерывности функции:
были введены при рассмотрении второго и третьего замечательных пределов. Поскольку логарифм – функция непрерывная, перестановка местами логарифма и предела следует из первого определения непрерывности функции: 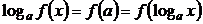 .
.
12. 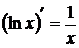 .
.
Формула является следствием предыдущей формулы.
13. 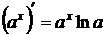 .
.
Пусть 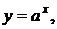 тогда
тогда 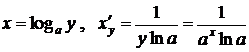 , следовательно,
, следовательно,
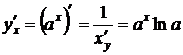 .
.
14. 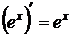 . Формула является следствием предыдущей.
. Формула является следствием предыдущей.
Для вычисления производных большинства функций достаточно знать таблицу производных элементарных функций и уметь применять правила дифференцирования. Иногда удобно готовить функцию к дифференцированию, приводя ее к наиболее удобному для вычисления производной виду.
Примеры вычисления производных
1. 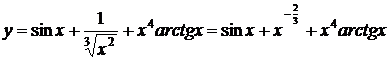 ,
,
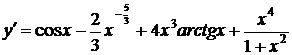 .
.
При вычислении производной использовались правила производной от суммы и произведения, таблица производной. Второе слагаемое функции 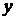 преобразовано к более удобному для дифференцирования виду.
преобразовано к более удобному для дифференцирования виду.
2. 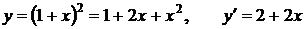 .
.
3. 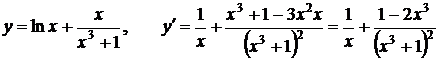 .
.
В вышеприведенных примерах дифференцируемые функции являлись либо комбинациями простых функций, либо приводились к таким комбинациям.
При вычислении производных сложных функций существенно используется правило дифференцирования сложных функций с фактическим или мысленным введением одного и более промежуточных аргументов.
4. 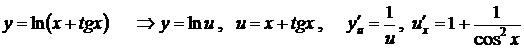 ,
,
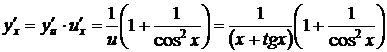 .
.
5. 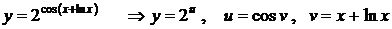 ,
,
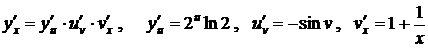 ,
,
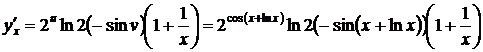 .
.
Из последних двух примеров следует, что при вычислении производных сложных функций вначале вводится необходимое количество промежуточных аргументов, после чего функции становятся простыми, это позволяет произвести дифференцирование, затем для получения ответа необходимо избавиться от этих промежуточных аргументов. Это обстоятельство приводит к идее о "мысленном" введении этих промежуточных аргументов, тогда нет необходимости избавляться от них в конце решения.
В этом случае вводится следующее правило вычисления производных: производная функции представляет собой произведение производной по сложному аргументу на производную от этого сложного аргумента. При этом обычно действуют в направлении, противоположном вычислению функции.
Рассмотрим вначале те же примеры.
4'. Функция 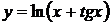 вычисляется следующим образом. Вначале вычисляется выражение
вычисляется следующим образом. Вначале вычисляется выражение 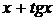 , затем логарифм этого выражения. Дифференцируем в противоположном направлении. Производная от логарифма умножается на производную от выражения под знаком логарифма.
, затем логарифм этого выражения. Дифференцируем в противоположном направлении. Производная от логарифма умножается на производную от выражения под знаком логарифма.
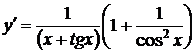 .
.
При этом мысленно вводится аргумент 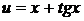 . Следует отметить, что результат в последнем случае получается гораздо быстрее, чем в первом.
. Следует отметить, что результат в последнем случае получается гораздо быстрее, чем в первом.
5'. 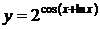 . При вычислении функции определяем вначале выражение
. При вычислении функции определяем вначале выражение 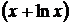 , затем косинус этого выражения, после чего получаем значение показательной функции. Вычисляем производную в обратном порядке: вначале производная от показательной функции, умножаем ее на производную от косинуса, и, наконец, на производную от суммы функций. Тогда
, затем косинус этого выражения, после чего получаем значение показательной функции. Вычисляем производную в обратном порядке: вначале производная от показательной функции, умножаем ее на производную от косинуса, и, наконец, на производную от суммы функций. Тогда
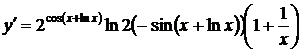 .
.
Мысленное введение промежуточных аргументов в процессе дифференцирования делает функции, как бы, простыми, что позволяет использовать таблицу производных.
6. 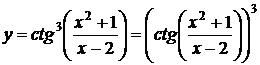 ,
,
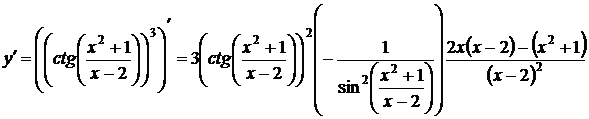 ,
,
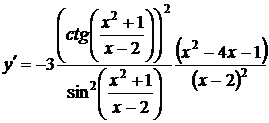 .
.
7. 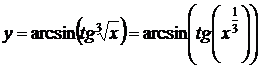 ,
,
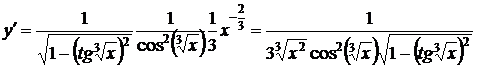 .
.
Примеры для самостоятельного решения
Вычислить 
7.1 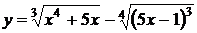 , 7.2
, 7.2 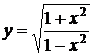 , 7.3
, 7.3 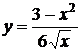 ,
,
7.4. 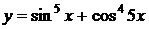 , 7.5
, 7.5 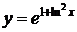 , 7.6
, 7.6  ,
,
7.7 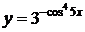 , 7.8
, 7.8 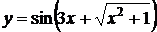 , 7.9
, 7.9 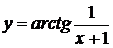 .
.
В этой главе примеры для самостоятельной работы приводятся без ответов, ибо ответ в данном случае является решением задачи.
