Схема нахождения наибольшего и наименьшего значений функции .
1. Найти О.О.Ф.
2. Найти 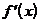 в О.О.Ф.
в О.О.Ф.
3. Найти критические точки в О.О.Ф.:
4. а).в которых выполняется равенство 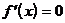 ;
;
5. б) в которых 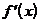 не существует.
не существует.
6. Изобразить на числовой оси О.О.Ф. и все ее критические точки.
7. Определить интервалы знакопостоянства производной в каждом из промежутков на которые критические точки разбивают О.О.Ф.
8. На основании достаточных условий экстремума сделать заключение о экстремуме функции в каждой из указанных в п.3 критических точках.
9. Найти значения функции в критических точках внутри промежутка и на концах промежутка (если это числа).
10. Из всех найденных значений в п.7 выбрать наибольшее и наименьшее значения.
Пример 21. Найти наибольшее и наименьшее значения функции 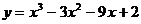 на отрезке [-2; 2].
на отрезке [-2; 2].
Решение. О.О.Ф.: х Î R;
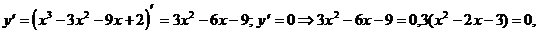
х1 = -1, х2 = 3 – критические точки; x1 = -1 Î [-2; 2], x2 = 3 Ï [-2; 2].
х1 = -1 – единственная критическая точка на [-2; 2].

у(-1)=(-1)3-3(-1)2-9(-1)+2=-1-3+9+2=7 (наибольшее);
у(2)= (2)3-3(2)2-9×(2)+2=8-12-18+2=-20 (наименьшее);
у(-2)= (-2)3-3×(-2)2-9×(-2)+2=-8-12+18+2=0. Ответ: 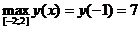
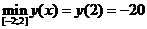
Пример 22. Найти наибольшее и наименьшее значения функции 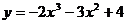 на промежутке [1; 3).
на промежутке [1; 3).
Решение. О.О.Ф.: x Î R;
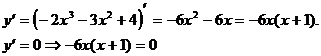
х1 = 0, х2 =-1 – критические точки.

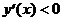 на [1; 3).
на [1; 3).
На промежутке [1; 3) данная функция убывает:
у(1) = -2×(1)3 -×3(1)2 + 4 = -2-3+4 = -1.
Наибольшее значение функция достигает на левом конце промежутка:
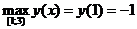 .
.
Наименьшее значение в промежутке [1; 3) функция не достигает, так как точка х =3 не принадлежит этому промежутку.
Ответ: 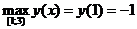
Пример 23. Требуется огородить проволочной сеткой длины 32 м прямоугольный участок, прилегающий к стене. Найти размеры участка, при которых его площадь будет наибольшей.
 |
Решение. Обозначим стороны прямоугольника через АВ = СD = x, BC = AD = y. Тогда его площадь S = xy.
Так как 2х + у = 32, получим 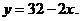 Тогда
Тогда 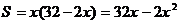 . Найдем О.О.Ф. площади:
. Найдем О.О.Ф. площади:
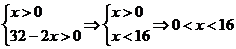 .
.
Найдем наибольшее значение функции S на интервале (0; 16).
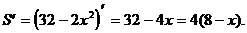
х = 8 – единственная критическая точка.

х = 8 – единственная точка максимума, значит
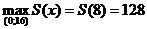 .
.
Размеры участка: ширина – х = 8; длина – у = 32-16=16.
Ответ: 8 м и 16 м.
Задачи раздела I.
1. Найти производную функции в точке x0:
1) 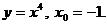
2) 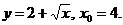
3) 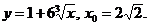
4) 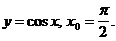
5) 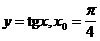
6) 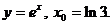
7) 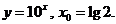
8) 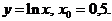
9) 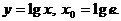
2. Найти производную функции, предварительно приведя ее к виду kxm(mÎZ).
1) 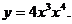 3)
3) 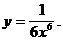
2) 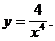 4)
4) 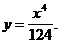
3. Приведя функцию к к виду kxa(aÎQ) найти ее производную.
1) 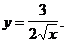
2) 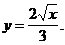
3) 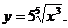
4) 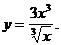
5) 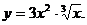
4. Используя формулу производной от суммы найти производную функции:
1) 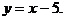
2) 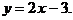
3) 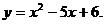
4) 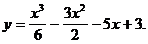
5) 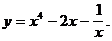
6) 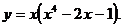
7) 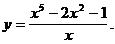
5. Используя формулы производной произведения или частного, найти производную функции:
1) 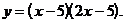
2) 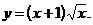
3) 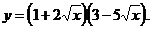
4) 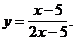
5) 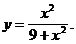
6) 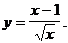
6. Используя правило дифференцирования сложной функции, найти производную функции:
1) 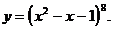
2) 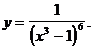
3) 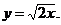
4) 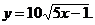
5) 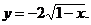
6) 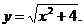
7) 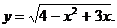
7. Найти критические точки функции:
1) 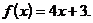
2) 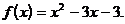
3) 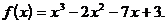
4) 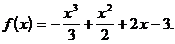
5) 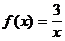
6) 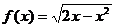
8. Найти промежутки возрастания и убывания функции:
1) 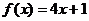
2) 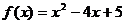
3) 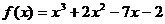
4) 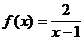
5) 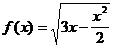
9. Найти точки экстремума и экстремумы функции.
1) 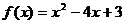
2) 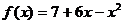
3) 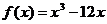
4) 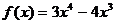
5) 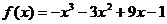
6) 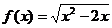
10. Найти наибольшее и наименьшее значения функции на промежутке.
1) 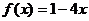 на [-3; 2]
на [-3; 2]
2) 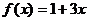 на [-2; 3)
на [-2; 3)
3) 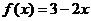 на (-1; 2]
на (-1; 2]
4) 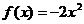 на [-2; 1]
на [-2; 1]
5) 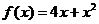 на [-1; 0]
на [-1; 0]
6) 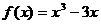 на [0; 3]
на [0; 3]
11. Периметр прямоугольника равен 40. Найти его стороны, при которых его площадь будет наибольшей.
Задачи раздела II.
1. Найти производную функции в точке x0:
1) 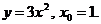
2) 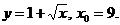
3) 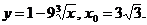
4) 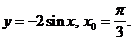
5) 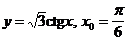
6) 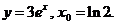
7) 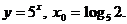
8) 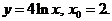
9) 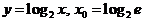
2. Найти производную функции, предварительно приведя ее к виду kxm(mÎZ).
1) 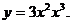
2) 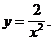
3) 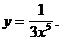
4) 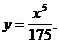
3. Приведя функцию к к виду kxa(aÎQ) найти ее производную.
1) 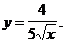
2) 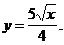
3) 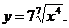
4) 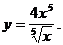
5) 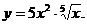
4. Используя формулу производной от суммы найти производную функции:
1) 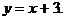
2) 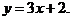
3) 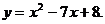
4) 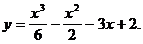
5) 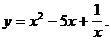
6) 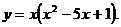
7) 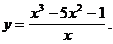
5. Используя формулы производной произведения или частного, найти производную функции:
1) 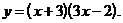
2) 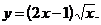
3) 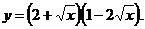
4) 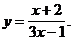
5) 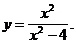
6) 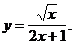
6. Используя правило дифференцирования сложной функции, найти производную функции:
1) 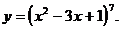
2) 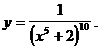
3) 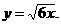
4) 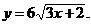
5) 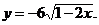
6) 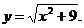
7) 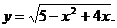
7. Найти критические точки функции:
1) 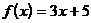
2) 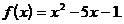
3) 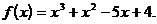
4) 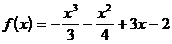
5) 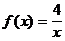
6) 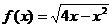
8. Найти промежутки возрастания и убывания функции:
1) 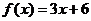
2) 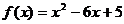
3) 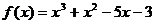
4) 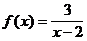
5) 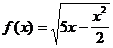
9. Найти точки экстремума и экстремумы функции.
1) 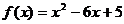
2) 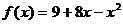
3) 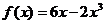
4) 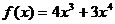
5) 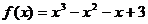
6) 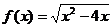
10. Найти наибольшее и наименьшее значения функции на промежутке.
1) 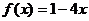 на [-3; 2]
на [-3; 2]
2) 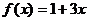 на [-2; 3)
на [-2; 3)
3) 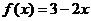 на (-1; 2]
на (-1; 2]
4) 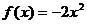 на [-2; 1]
на [-2; 1]
5) 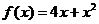 на [-1; 0]
на [-1; 0]
6) 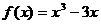 на [0; 3]
на [0; 3]
Решение задач раздела I.
1.
1) 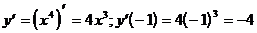
2) 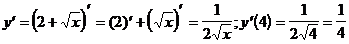
3) 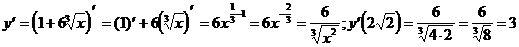
4) 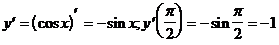
5) 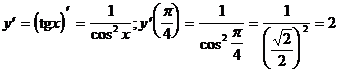
6) 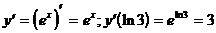
7) 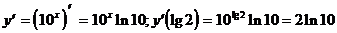
8) 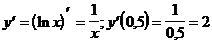
9) 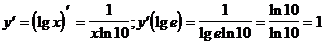
2.
10) 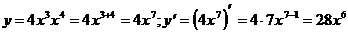
11) 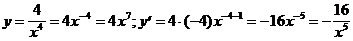
12) 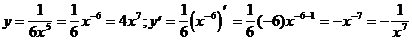
13) 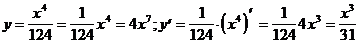
3.
1) 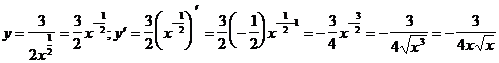
2) 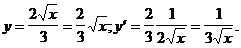
3) 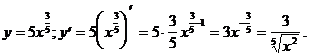
4) 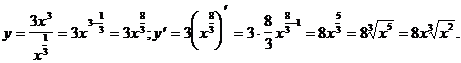
5) 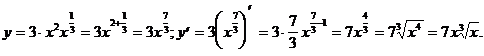
4.
1) 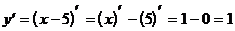
2) 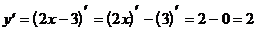
3) 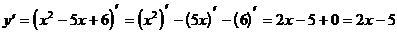
4) 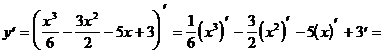
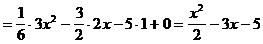
5) 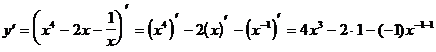
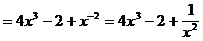
6) 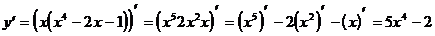
7) 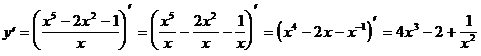
5.
1) 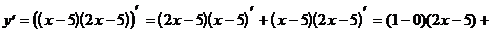
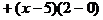
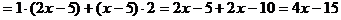
2) 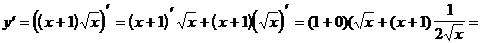
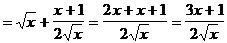
3) 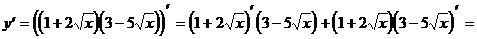
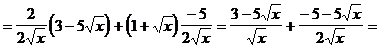
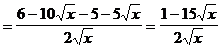
4) 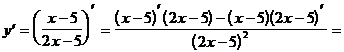
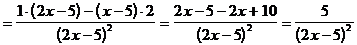
5) 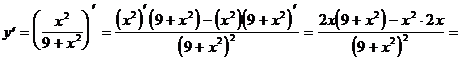
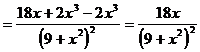
6) 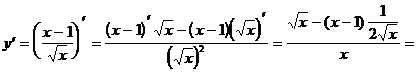
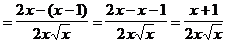
6.
1) 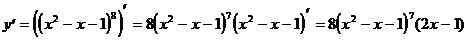
2) 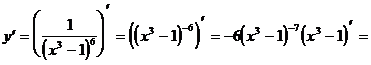
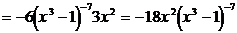
3) 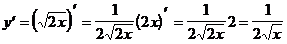
4) 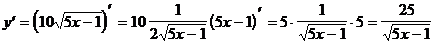
5) 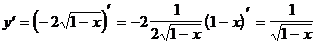
6) 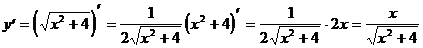
7) 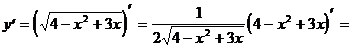
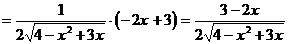
7.
1) О.О.Ф. xÎR; 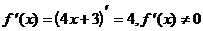 для всех x Î R. Ответ: критических точек нет.
для всех x Î R. Ответ: критических точек нет.
2) О.О.Ф. xÎR; 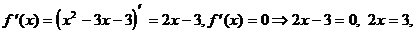
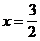 Î О.О.Ф.
Î О.О.Ф.
Ответ: 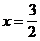 .
.
3) О.О.Ф. xÎR; 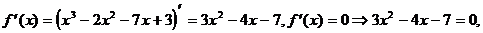 D = 16 + 84 = 100>0;
D = 16 + 84 = 100>0; 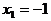 Î О.О.Ф.,
Î О.О.Ф., 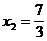 Î О.О.Ф. Ответ:
Î О.О.Ф. Ответ: 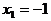 ,
, 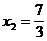
4) О.О.Ф. xÎR; 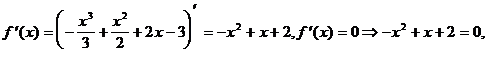
D = 1+8=9>0; 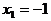 Î О.О.Ф.,
Î О.О.Ф., 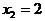 Î О.О.Ф. Ответ:
Î О.О.Ф. Ответ: 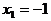 ,
, 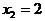
5) О.О.Ф. x¹0; 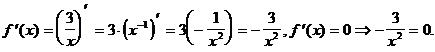
При х = 0 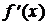 не существует. х = 0 Ï О.О.Ф. Ответ: критических точек нет.
не существует. х = 0 Ï О.О.Ф. Ответ: критических точек нет.
6) О.О.Ф. 2х - х2 ³ 0; х(2-х)³0 Þ 0£ х£ 2.
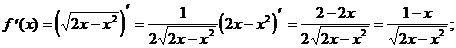
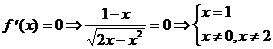
При х = 1 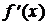 =0. При х = 0 и х = 2
=0. При х = 0 и х = 2 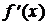 не существует.
не существует.
х1 = 1 Î О.О.Ф., х2 = 0 Î О.О.Ф., х3 = 2 Î О.О.Ф. Ответ: х1 = 1, х2 = 0, х3 = 2.
8.
1) О.О.Ф.: хÎR; 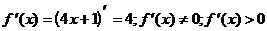 для всех хÎR.
для всех хÎR.
Ответ: возрастает для всех хÎR.
2) О.О.Ф.: хÎR; 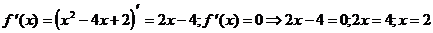 ÎО.О.Ф.
ÎО.О.Ф.
 Ответ: убывает на (-¥; 2)
Ответ: убывает на (-¥; 2)
возрастает на (2; +¥)
3) О.О.Ф.: хÎR; 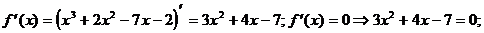 D=16+84=100>0; х1 = -7/3 Î О.О.Ф., х2 = 1 Î О.О.Ф.
D=16+84=100>0; х1 = -7/3 Î О.О.Ф., х2 = 1 Î О.О.Ф.
 Ответ: возрастает на (-¥; -7/3), (1; +¥)
Ответ: возрастает на (-¥; -7/3), (1; +¥)
убывает на (-7/3; 1)
4) О.О.Ф.: х¹ 1; 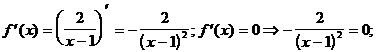
При х = 1 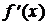 не существует х = 1 ÎО.О.Ф.
не существует х = 1 ÎО.О.Ф.
 Ответ: убывает на (-¥; 1), (1; +¥)
Ответ: убывает на (-¥; 1), (1; +¥)
5) О.О.Ф.: 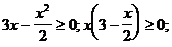 0£х£6.
0£х£6.
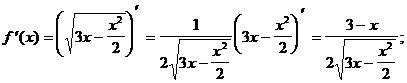
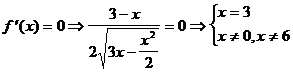
При х = 3ÎО.О.Ф. 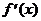 =0. При х = 0ÎО.О.Ф., х = 6ÎО.О.Ф.
=0. При х = 0ÎО.О.Ф., х = 6ÎО.О.Ф. 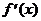 не существует.
не существует.

Ответ: возрастает на (0; 3),
убывает на (3; 6).
9.
1) О.О.Ф.: хÎR; 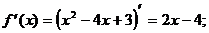
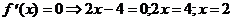 ÎО.О.Ф.
ÎО.О.Ф.

хmin= 2; уmin = y(xmin) = у(2) = 22-4×2+3=4-8+3=-1.
Ответ: хmin= 2;
уmin = -1.
2) О.О.Ф.: хÎR; 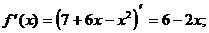
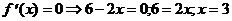 ÎО.О.Ф.
ÎО.О.Ф.

хmax= 3; уmax = y(xmax) = у(3) = 7+6×3-32=7+18-9=16
Ответ: хmax= 3;
уmax = 16
3) О.О.Ф.: хÎR; 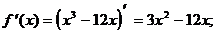
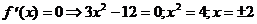 ÎО.О.Ф.
ÎО.О.Ф.

хmax= -2; уmax = y(xmax) = у(-2) = (-2)3-12×(-2)=-8+24=6
хmin= 2; уmin = y(xmin) = у(2) = 23-12×(2)=8-24=-6.
Ответ: хmax= -2; уmax =6
хmin= 2; уmin =-6.
4) О.О.Ф.: хÎR; 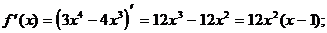
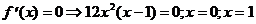 ÎО.О.Ф
ÎО.О.Ф

хmin= 1; уmin = y(xmin) = у(1) = 3×14-4×13=3-4=-1.
Ответ: хmin= 1; уmin =-1.
5) О.О.Ф.: хÎR; 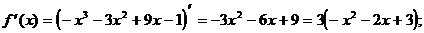
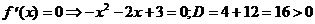 х1 =-3ÎО.О.Ф., х2 =1ÎО.О.Ф
х1 =-3ÎО.О.Ф., х2 =1ÎО.О.Ф

хmin= -3; уmin = y(xmin) = у(-3) = -(-3)3-3(-3)2+9(-3)-1=27-27-27-1=-28;
хmax= 1; уmax = y(xmax) = у(1) = -(1)3-3(1)2+9(1)-1=-1-3+9-1=4.
Ответ: хmin= -3; уmin =-28;
хmax= 1; уmax = 4.
6) О.О.Ф.: х2-2х³0, х(х-2)³0 Þ х Î (-¥; 0] È [2; +¥).
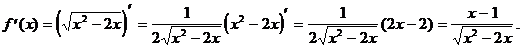
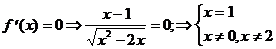
х = 1 Ï О.О.Ф.

Ответ: экстремумов нет.
10.
1) О.О.Ф.: хÎR; 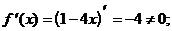 критических точек нет.
критических точек нет.
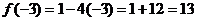 – наибольшее значение
– наибольшее значение
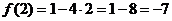 – наименьшее значение.
– наименьшее значение.
Ответ: 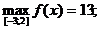
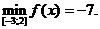
2) О.О.Ф.: хÎR; 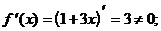 критических точек нет.
критических точек нет.
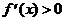 для всех хÎR Þ f(x) возрастает на [-2; 3).
для всех хÎR Þ f(x) возрастает на [-2; 3).
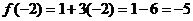 – наименьшее значение.
– наименьшее значение.
Наибольшее значение данная функция не достигает.
Ответ: 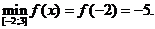
3) О.О.Ф.: хÎR; 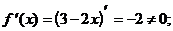 критических точек нет.
критических точек нет.
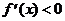 для всех хÎR Þ f(x) убывает на [-1; 2).
для всех хÎR Þ f(x) убывает на [-1; 2).
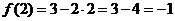 – наименьшее значение.
– наименьшее значение.
Наибольшее значение данная функция не достигает.
Ответ: 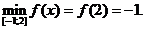
4) О.О.Ф.: хÎR; 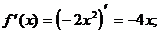
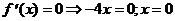 Î О.О.Ф.
Î О.О.Ф.
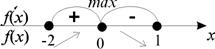
хтах = 0 – единственная точка экстремума.
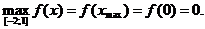
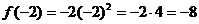 – наименьшее значение;
– наименьшее значение;
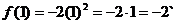
Ответ: 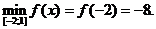
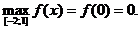
5) О.О.Ф.: хÎR; 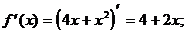
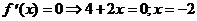 Ï [-1; 0].
Ï [-1; 0].
f(-1)=4×(-1)+(-1)2=-4+1=-3 – наименьшее значение;
f(0)=4×(0)+(0)2=0 – наибольшее значение.
Ответ: 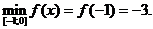
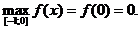
6) О.О.Ф.: хÎR; 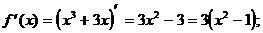
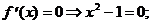 х = 1 Î [0; 3]; x = -1 Ï [0; 3].
х = 1 Î [0; 3]; x = -1 Ï [0; 3].
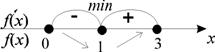
f(1)=1-3=-2 – наименьшее значение;
f(0)=0;
f(3)=27-9=18 – наибольшее значение.
Ответ: 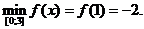
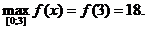
11.
 |
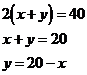
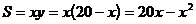
О.О.Ф. площади: 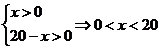 .
.
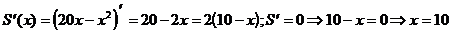 ÎО.О.Ф.
ÎО.О.Ф.
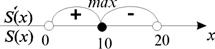
хтах = 10 – единственная точка экстремума.
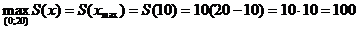
Стороны прямоугольника: х = 10, у = 20-10=10.
Ответ: квадрат со стороной 10.
Ответы к задачам раздела II.
1.
1) 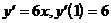 ;
;
2) 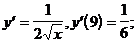
3) 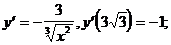
4) 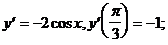
5) 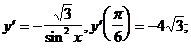
6) 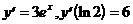 ;
;
7) 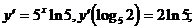
8) 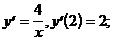
9) 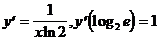 .
.
2.
1) 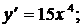 2)
2) 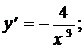 3)
3) 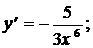 4)
4) 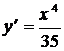 .
.
3.
1) 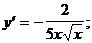 2)
2) 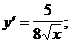 3)
3) 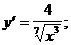 4)
4) 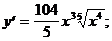 5)
5) 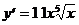 .
.
4.
1) 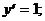
2) 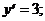
3) 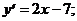
4) 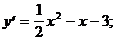
5) 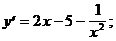
6) 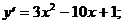
7) 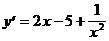 .
.
5.
1) 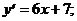
1) 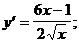
2) 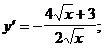
3) 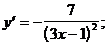
4) 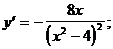
5) 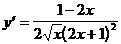 .
.
6.
1) 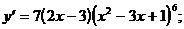
2) 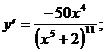
3) 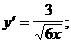
4) 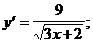
5) 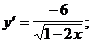
6) 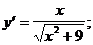
7) 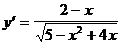 .
.
7.
1) Критических точек нет;
2) {2,5};
3) {-5/3; 1};
4) {-3; 2};
5) критических точек нет;
6) {0; 2; 4}.
8.
1) возрастает на (-¥; +¥);
2) убывает на (-¥; 3),
возрастает на (3; +¥);
3) возрастает на (-¥; -5/3), (1; +¥),
убывает на (-5/3; 1);
4) убывает на (-¥; 2), (2; +¥);
5) возрастает на (-¥; 5),
убывает на (5; +¥).
9.
1) xmin = 3, ymin = -4;
2) xmax = 4, ymax = 25;
3) xmin = -1, ymin = -4,
xmax = 1, ymax = 4;
4) xmin = -1, ymin = -1;
5) xmin = 1, ymin = 2,
xmax = 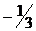 , ymax =
, ymax = 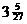 ;
;
6) экстремумов нет.
10.
1) 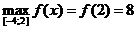 ,
,
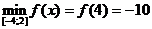 ;
;
2) 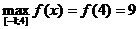 ,
,
наименьшего нет;
3) 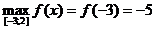 ,
,
наименьшего нет;
4) 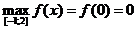 ,
,
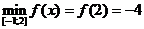 ;
;
5) 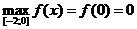 ,
,
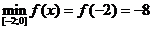 ;
;
6) 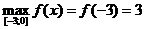 ,
,
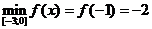 .
.
Квадрат со стороной 9.
