Схема исследования функции на монотонность.

1. Найти О.О.Ф.

2. Найти 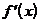в О.О.Ф.

3. Найти критические точки в О.О.Ф.:

4. а).в которых выполняется равенство ;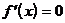

5. б) в которых 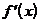не существует.

6. Изобразить на числовой оси О.О.Ф. и все ее критические точки.

7. Определить интервалы знакопостоянства производной в каждом из промежутков на которые критические точки разбивают О.О.Ф.

8. На основании достаточных условий монотонности сделать заключение о характере монотонности в каждом из указанных в п.5 промежутков.

Пример 13. Исследовать на монотонность функцию .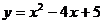

Решение.

1). Данная функция определена на всей числовой прямой (х Î R).

2). Найдем производную:

.

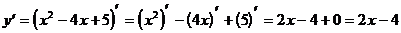3). а) из уравнения 2х - 4 = 0 находим х = 2;

б) 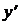существует при всех х. Значит, х = 2 – единственная критическая точка.

4). Критическая точка х = 2 разбивает числовую ось на два промежутка (-¥; 2) и

(2; +¥).

5). Определим интервалы знакопостоянства производной :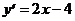

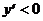на промежутке (-¥; 2), так как ;

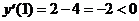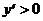на промежутке (2; +¥), так как .

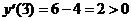Ответ: убывает на (-¥; 2),

возрастает на (2; +¥).

Пример 14. Найти промежутки монотонности функции .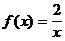

Решение. О.О.Ф. – вся числовая прямая за исключением точки х = 0.

Находим .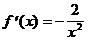

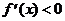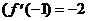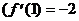Точки х = 0 (в ней производная не существует) не принадлежит О.О.Ф. Поэтому на числовой оси отмечаем ее «пустой» точкой. Очевидно, что при всех х ¹ 0 и ), то есть данная функция убывает в промежутках (-¥; 0) и (0; +¥).

Ответ: убывает в промежутках (-¥; 0) и (0; +¥).

Пример 17. Найти промежутки возрастания (убывания) функции .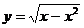

Решение. Найдем О.О.Ф. Для этого необходимо решить неравенство: 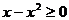или 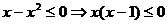. Уравнение 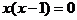имеет корни х₁ = 0 и х₂ = 1. Неравенство 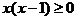справедливо прямоугольник всех значениях х в промежутке [0; 1]. Следовательно, функция 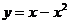определена в промежутке [0; 1].

Найдем производную функции :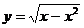

.

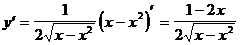Критические точки: х₁ = 1/2, х₂ = 0, х₃ = 1 (В точке х = 1/2 выполняется равенство 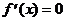, а в точках х = 0 и х = 1 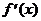не существует) – принадлежат области определения функции 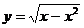и разбивает ее на два промежутка: 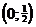и .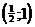

В промежутке (0; 1) выражение в знаменателе производной 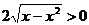, поэтому знак производной определяется знаком числителя 1 - 2х:

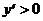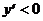на и на .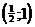

Следовательно, функция 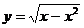возрастает на промежутке 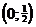и убывает на промежутке .

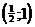На промежутках (-¥; 0) и (1; +¥) функция 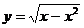не определена.

Ответ: возрастает на промежутке ;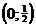

убывает на промежутке .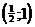

Исследование функции на экстремум.

Справочный материал.

1. Точка x=x₀ из области определения функции f(x) называется точкой минимума (максимума) этой функции, если у этой точки существует окрестность такая, что для всех x¹x₀ из этой окрестности выполняется неравенство .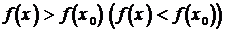

2. Точки максимума 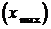и минимума 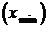функции объединяются общим термином – точки экстремума.

3. Значения функции в точке экстремума называются соответственно максимумом 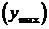и минимумом 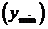функции (или экстремумами самой функции).

4. Функция y=f(x), график которой расположен на рис.1, в точках x₁ и x₃ имеет минимумы 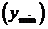, а в точках x₂ и x₄ – максимумы 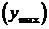. Точки a и b не считаются точками экстремума функции f(x), т.к. у этих точек нет окрестности, целиком входящей в область определения функции.

5. Исследование функции на экстремум основано на следующих двух утверждениях:

а). Необходимое условие экстремума. Если точка x₀ является точкой экстремума функции y=f(x), то производная в этой точке равна нулю: .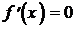

б). Достаточные условие экстремума.

Если в окрестности точки x₀ производная меняет знак с плюса на минус, то x₀ есть точка максимума.

Если в окрестности точки x₀ производная меняет знак с минуса на плюс, то x₀ есть точка минимума.