Векторное произведение. Геометрический смысл векторного произведения.

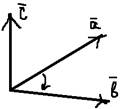
Тройка векторов , , (некомпланарных) называется правой, если она ориентирована по правилу правого винта.

Правило левого винта

Под векторным произведением двух векторов и понимается вектор = * , для которого:

1)Модуль равен площади параллелограмма, построенного на данных векторах, т.е. модуль = * *sinϕ, где ϕ угол между векторами

2)Вектор 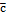одновременно 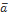⊥и и

3)если векторынеколлинеарны, то вектора , , 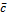образуют правую тройку векторов

Свойства векторного произведения:

1. * =- *

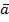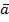
2. 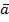* 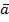=0

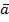3.(λ 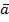)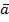* =λ( * )= *(λ ), где λ-const

4.( + )* = * + *

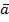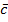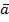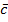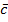
5. 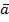// 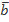, если * 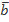=0

= + +

= + +

* =

* =

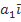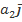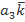
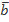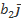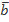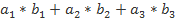
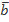Из определения векторного произведения ,построенного на векторах 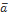и равна

Геометрический смысл векторного произведения:

По определению длина векторного произведения векторов равна 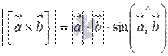. А из курса геометрии средней школы нам известно, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними. Следовательно, длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы 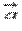и , если их отложить от одной точки. 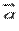Другими словами, длина векторного произведения векторов и 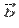равна площади параллелограмма со сторонам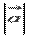и и 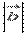и углом между ними, равным . В этом состоит геометрический смысл векторного произведения.

13. Смешанное произведение. Условие компланарности векторов.

Смешанное произведение векторов — скалярное произведение вектора на векторное произведение векторов и .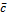

Смешанное произведение векторов равно определителю матрицы, составленной из этих векторов.

Смешанное произведение векторов = {ax; ay; az}, = {bx; by; bz} и 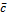= {cx; cy; cz} в декартовой системе координат можно вычислить, используя следующую формулу:

· [ х ] =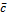

Свойства:

1)Геометр. смысл смешанного произведения. Модуль смешанного произведения 3х векторов вектора , и 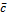равен объёму параллелепипеда, образованного этими векторами:

Vпарал = · [ × ]

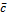2) Геометрич.смысл смешанного произведения. Объем пирамиды образованной 3мя векторами , и 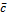равен 1/6 части от модуля смешанного произведения этих векторов:

Vпир = 1/6*| · [ × ]|

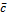3) Если смешанного произведения трех не нулевых векторов равно нулю, то эти вектора компланарные.

4) · [ × ] = · ( · ) - · ( · )

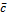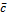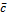5) · [ × ] = · [ × ] = · [ × ] = · [ × ] = · [ × ] = · [ × ]

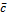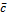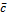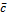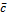Условия компланарности векторов:

Для 3-х векторов:

Три вектора компланарны если их смешанное произведение равно нулю.

Для 3-х векторов:

Три вектора компланарны если они линейно зависимы.

Для n векторов:

Вектора компланарны если среди них не более двух линейно независимых векторов.

14. Прямая на плоскости. Виды уравнений прямой линии.Взаимное расположение прямых на плоскости.

Определение. Любая прямая на плоскости может быть задана уравнением 1 порядка: Ах + Ву + С = 0, (А ≠0, В ≠ 0). Это уравнение 1 порядка называется общим уравнением прям. В зависимости от значений постоянных А,В и С возможны следующие частные случаи:

• C = 0, А ≠0, В ≠ 0 – прямая проходит через начало координат

• А = 0, В ≠0, С ≠0 { By + C = 0}- прямая параллельна оси Ох

• В = 0, А ≠0, С ≠ 0 { Ax + C = 0} – прямая параллельна оси Оу

• В = С = 0, А ≠0 – прямая совпадает с осью Оу

• А = С = 0, В ≠0 – прямая совпадает с осью Ох

1)Уравнение прямой по точке и вектору нормали:

Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой , заданной уравнением Ах + Ву + С = 0.

2) Уравнение прямой, проходящая через 2 точки:

Пусть в пространстве заданы 2 точки M ₁ (x ₁ , y ₁ , z ₁) и M₂ (x ₂, y ₂ , z ₂), тогда уравнение прямой, проходящая через эти точки: X-X1/X2-X1=Y-Y1/Y2-Y1=Z-Z1/Z2-Z1. Если какой- либо из знаменателяравен0, следует приравнять 0 соответ. числитель. На плоскости записанное выше уравнение прямой упрощается: Y-Y1=Y2-Y1/X2-X1*(X-X1), если х ₁ ≠ х₂ и х = х ₁ , если х ₁ = х₂ . Дробь Y2-Y1/X2-X1= k называется угловой коэффициент прямой.

3)Уравнение прямой по точке и угловому коэффициенту:

Если общее уравнение прямой Ах + Ву + С = 0 привести к виду: Y=-A/B*X-C/B, и обозначить –A/B=k, -C/B=b, т.еy=kx+b, то полученное уравнение называется уравнением прямой с угловым коэффициентомk.

4)Уравнение прямой по точке и направляющему вектору:

по аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание прямой через точку и направляющий вектор прямой.

Опр.: Каждый ненулевой вектор ( α₁ , α₂ ), компоненты которого удовлетворяют условию А α₁ + В α₂ = 0 называется направляющим вектором прям. Ах + Ву + С=0.

5)Уравнение прямой в отрезках:

Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим: -A/C*X-B/C*Y=1 или x/a+y/b=1, где a= -C/A, b= -C/B. Геометрический смысл коэффициентов в том, что коэффициент аявляется координатой точки пересечения прямой с осью Ох, а b– координатой точки пересечения прямой с осью Оу.

6)Нормальное уравнение прямой: Если обе части уравнения Ах + Ву + С = 0 разделить на число µ= 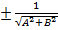, которое называется нормирующем множителем , то получим: xcosφ + ysinφ - p = 0 –нормальное уравнение прямой. Знак ± нормирующего множителя надо выбирать так, чтобы μ * С < 0. р – длина перпендикуляра, опущенного из начала координат на прямую, а φ - угол, образованный этим перпендикуляром с положительным направлением оси Ох.

Взаимное расположение прямых на плоскости:

Возможны 3 варианта взаимного расположения прямой и плоскости:

1)Прямая параллельна плоскости, если она не имеет с плоскостью общих точек.

2)Прямая пересекает плоскость, если она имеет с плоскостью ровно 1 общую точку.

3)Прямая лежит в плоскости, если каждая точка прямой принадлежит этой плоскости.

Признак параллельности прямой и плоскости. Если прямая l параллельна некоторой прямой, лежащей в плоскости, то прямая l параллельна этой плоскости. Важным частным случаем пересечения прямой и плоскости является их перпендикулярность.

Определение. Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости. Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.