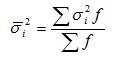Средняя гармоническая величина
Если по условиям задачи необходимо, чтобы неизменной оставалась при осреднении сумма величин, обратных индивидуальным значениям признака, то средняя величина является гармонической средней.
Средняя гармоническая величина, как и средняя арифметическая может быть простой и взвешенной. Если веса у каждого значения признака равны, то можно использовать среднюю гармоническую простую:
.
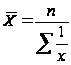Однако в статистической практике чаще применяется средняя гармоническая взвешенная:
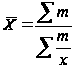, где m = xf ,
она используется, как правило, при расчете общей средней из средних групповых.
Средняя гармоническая имеет более сложную конструкцию, чем средняя арифметическая. Среднюю гармоническую применяют для расчетов тогда, когда в качестве весов используются не единицы совокупности – носители признака, а произведения этих единиц на значения признака (т.е. m = Xf). К средней гармонической простой следует прибегать в случаях определения, например, средних затрат труда, времени, материалов на единицу продукции, на одну деталь по двум (трем, четырем и т.д.) предприятиям, рабочим, занятым изготовлением одного и того же вида продукции, одной и той же детали, изделия.
Средняя геометрическая величина
Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных величин, то следует применить геометрическую среднюю величину.
Ее формула такова:
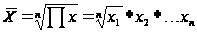, для простой.
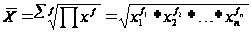, для взвешенной.
Средняя квадратическая величина
Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин, то средняя будет являться квадратической средней величиной.
Ее формула такова:
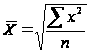, для простой.
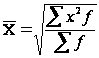, для взвешенной.
Структурные средние величины
Особый вид средних величин – структурные средние – применяется для изучения внутреннего строения рядов распределения значений признака, а также для оценки средней величины (степенного типа), если по имеющимся статистическим данным ее расчет не может быть выполнен (например, если бы в рассмотренном примере отсутствовали данные и об объеме производства, и о сумме затрат по группам предприятий).
В качестве структурных средних применяют показатели моды и медианы.
Мода и медиана определяются лишь структурой распределения. Поэтому их именуют структурными позиционными средними. Медиану и моду часто используют как среднюю характеристику в тех совокупностях, где расчет средней степенной невозможен или нецелесообразен.
Б-49 Изучение вариации (колеблемости, рассеивания) (см. Показатели вариации) признака по всей совокупности в целом, предусматривает изучение вариации для каждой из составляющих ее групп, а также между этими группами. В простейшем случае, когда совокупность разбита на группы по одному фактору, изучение вариации достигается посредством исчисления и анализа трех видов дисперсий: общей,межгрупповой ивнутригрупповой.
Общая дисперсияD(x)измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Она равна среднему квадрату отклонений отдельных значений признака (хi) от общей средней величины и может быть вычислена как: 1. простая дисперсия 2. взвешенная дисперсия
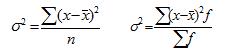
Межгрупповая дисперсия(факторная) характеризует систематическую вариацию результативного признака, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних от общей средней:
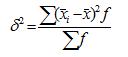
Внутригрупповая дисперсия(частная, остаточная, случайная) отражает случайную вариацию неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений отдельных значений признака внутри группы(хi) от средней арифметической этой группы (xср) (групповой средней) и может быть исчислена как:
1. простая дисперсия 2. взвешенная дисперсия
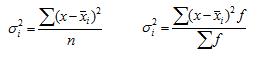
На основании внутригрупповой дисперсии по каждой группе можно определить общую среднюю из внутригрупповых дисперсий:
