Теорема 1. (Необходимое и достаточное условия возрастания функции)
- Если дифференцируемая функция y=f(x) возрастает на [a, b], то ее производная неотрицательна на этом отрезке, f '(x)≥ 0.
- Обратно. Если функция y=f(x) непрерывна на [a, b], дифференцируема на (a, b) и ее производная положительна на этом отрезке,f ' (x)≥ 0 для a<x<b, то f(x) возрастает на[a, b].
Доказательство.
- Докажем первую часть теоремы. Итак, пусть функция y=f(x) возрастает на [a, b]. Зафиксируем на этом отрезке произвольную точку x, придадим ей приращение Δx. Тогда если Δx>0, то x<x+Δx. Поэтому по определению возрастающей функции f(x)<f(x+Δx), то есть f(x+Δx) - f(x)>0. Но тогда и
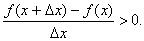 Аналогично, если Δx<0, то x>x+Δx и значит f(x+Δx)-f(x)<0, а
Аналогично, если Δx<0, то x>x+Δx и значит f(x+Δx)-f(x)<0, а 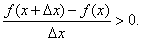
Переходя в этом равенстве к пределу при Δx→0, получим 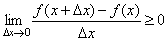 , то есть f '(x)≥0.
, то есть f '(x)≥0.
- Докажем вторую часть теоремы. Пусть f '(x)>0при всех x Î (a,b). Рассмотрим два любых значения x1 и x2 таких, что x1 < x2. Нужно доказать, что f(x1)< f(x2). По теореме Лагранжа существует такое число c Î (x1, x2), что
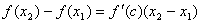 . По условию f '(x)>0, x1 – x2>0Þ
. По условию f '(x)>0, x1 – x2>0Þ  , а это и значит, что f(x) – возрастающая функция.
, а это и значит, что f(x) – возрастающая функция.
Аналогичная теорема имеет место и для убывающих функций.
Теорема 2. Если f(x) убывает на[a,b], то 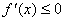 на этом отрезке. Если на этом отрезке. Если 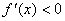 на (a; b), то f(x) убывает на [a, b],в предположении, чтоf(x) непрерывна на [a, b]. Доказанная теорема выражает очевидный геометрический факт. Если на [a, b] функция возрастает, то касательная к кривой y=f(x) в каждой точке этого отрезке образует острый угол с осью Ox или горизонтальна, т.е. tga≥0, а значит f '(x)≥0. Аналогично иллюстрируется и вторая часть теоремы. Таким образом, возрастание и убывание функции характеризуется знаком ее производной. Чтобы найти на каком промежутке функция возрастает или убывает, нужно определить, где производная этой функции только положительна или только отрицательна, то есть решить неравенства f '(x)>0 – для возрастания или f '(x)<0 – для убывания. Примеры. Определить интервалы монотонности функции. 3. на (a; b), то f(x) убывает на [a, b],в предположении, чтоf(x) непрерывна на [a, b]. Доказанная теорема выражает очевидный геометрический факт. Если на [a, b] функция возрастает, то касательная к кривой y=f(x) в каждой точке этого отрезке образует острый угол с осью Ox или горизонтальна, т.е. tga≥0, а значит f '(x)≥0. Аналогично иллюстрируется и вторая часть теоремы. Таким образом, возрастание и убывание функции характеризуется знаком ее производной. Чтобы найти на каком промежутке функция возрастает или убывает, нужно определить, где производная этой функции только положительна или только отрицательна, то есть решить неравенства f '(x)>0 – для возрастания или f '(x)<0 – для убывания. Примеры. Определить интервалы монотонности функции. 3. 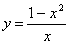 . Область определения заданной функции D(y) = (-∞; 0)È(0; +∞). . Область определения заданной функции D(y) = (-∞; 0)È(0; +∞). 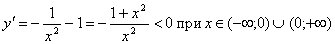 . Следовательно, f(x) – убывает на (-∞; 0) и (0; +∞). 4. . Следовательно, f(x) – убывает на (-∞; 0) и (0; +∞). 4. 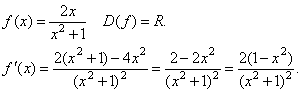 Найдем промежутки, на которых производная заданной функции положительна или отрицательна методом интервалов. Итак, f(x) – убывает на (–∞; –1] и [1; +∞), возрастает на отрезке [–1; 1]. 5. Найдем промежутки, на которых производная заданной функции положительна или отрицательна методом интервалов. Итак, f(x) – убывает на (–∞; –1] и [1; +∞), возрастает на отрезке [–1; 1]. 5. 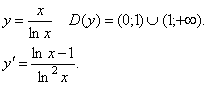 . Используя метод интервалов, получим f(x) убывает на (0; 1) и (1; e], возрастает на [e; +∞). . Используя метод интервалов, получим f(x) убывает на (0; 1) и (1; e], возрастает на [e; +∞). | 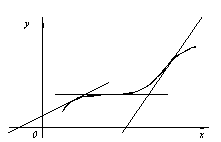  |
18 Максимум и минимум функции (точки экстремума). Необходимое условие экстремума.
Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).
Если дифференцируемая функция y=f(x) имеет в точке x= x0 экстремум, то ее производная в этой точке обращается в нуль.
Доказательство. Пусть для определенности в точке x0 функция имеет максимум. Тогда при достаточно малых приращениях Δx имеем f(x0+ Δx)<f(x0), т.е. 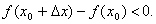 Но тогда
Но тогда
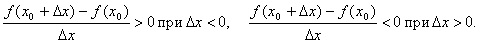
Переходя в этих неравенствах к пределу при Δx→ 0 и учитывая, что производная f '(x0) существует, а следовательно предел, стоящий слева, не зависит от того как Δx → 0, получаем: при Δx → 0 – 0 f'(x0) ≥ 0 а при Δx → 0 + 0 f'(x0) ≤ 0. Так как f '(x0) определяет число, то эти два неравенства совместны только в том случае, когда f '(x0) = 0.
Доказанная теорема утверждает, что точки максимума и минимума могут находиться только среди тех значений аргумента, при которых производная обращается в нуль. Мы рассмотрели случай, когда функция во всех точках некоторого отрезка имеет производную. Как же обстоит дело в тех случаях, когда производная не существует? Рассмотрим примеры. Примеры.
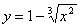 не имеет производной при x=0, так как не имеет производной при x=0, так как 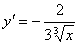 обращается в бесконечность приx=0. Но в этой точке функция имеет максимум. обращается в бесконечность приx=0. Но в этой точке функция имеет максимум. 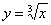 не имеет производной при x=0, так как не имеет производной при x=0, так как 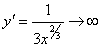 при x→0. В этой точке функция не имеет ни максимума, ни минимума. Действительно, f(x)=0 и при x<0f(x)<0, а при x>0f(x)>0. Таким образом, из приведенных примеров и сформулированной теоремы видно, что функция может иметь экстремум лишь в двух случаях: 1) в точках, где производная существует и равна нулю; 2) в точке, где производная не существует. Однако, если в некоторой точке x0 мы знаем, что f '(x0)=0, то отсюда нельзя делать вывод, что в точке x0 функция имеет экстремум. Например. при x→0. В этой точке функция не имеет ни максимума, ни минимума. Действительно, f(x)=0 и при x<0f(x)<0, а при x>0f(x)>0. Таким образом, из приведенных примеров и сформулированной теоремы видно, что функция может иметь экстремум лишь в двух случаях: 1) в точках, где производная существует и равна нулю; 2) в точке, где производная не существует. Однако, если в некоторой точке x0 мы знаем, что f '(x0)=0, то отсюда нельзя делать вывод, что в точке x0 функция имеет экстремум. Например. 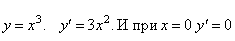 . Но точка x=0 не является точкой экстремума, поскольку слева от этой точки значения функции расположены ниже оси Ox, а справа выше. Значения аргумента из области определения функции, при которых производная функции обращается в нуль или не существует, называются критическими точками. . Но точка x=0 не является точкой экстремума, поскольку слева от этой точки значения функции расположены ниже оси Ox, а справа выше. Значения аргумента из области определения функции, при которых производная функции обращается в нуль или не существует, называются критическими точками. | 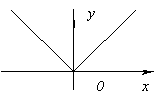 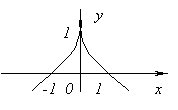 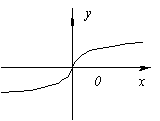 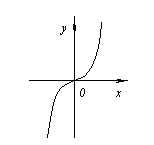 |
Из всего вышесказанного следует, что точки экстремума функции находятся среди критических точек, и, однако, не всякая критическая точка является точкой экстремума. Поэтому, чтобы найти экстремум функции, нужно найти все критические точки функции, а затем каждую из этих точек исследовать отдельно на максимум и минимум. Для этого служит следующая теорема.
19 Понятие критической точки. Первое достаточное условие экстремума. Наибольшее и наименьшее значения функции на отрезках.
Критической точкой дифференцируемой функции 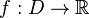 , где
, где 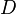 — область в
— область в 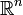 , называется точка, в которой все её частные производные обращаются в ноль. Это условие эквивалентно обращению в ноль дифференциала функции в данной точке, а также равносильно горизонтальности касательной гиперплоскости к графику функции. Это условие является необходимым (но не достаточным) для того, чтобы внутренняя точка области могла быть точкой локального минимума или максимума функции.
, называется точка, в которой все её частные производные обращаются в ноль. Это условие эквивалентно обращению в ноль дифференциала функции в данной точке, а также равносильно горизонтальности касательной гиперплоскости к графику функции. Это условие является необходимым (но не достаточным) для того, чтобы внутренняя точка области могла быть точкой локального минимума или максимума функции.
Значение функции в критической точке называется критическим значением. Согласно лемме Сарда, множество критических значений любой 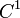 -гладкой функции
-гладкой функции 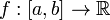 имеет нулевую меру Лебега (хотя критических точек при этом может быть сколько угодно, например, для функции
имеет нулевую меру Лебега (хотя критических точек при этом может быть сколько угодно, например, для функции 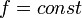 любая точка является критической).
любая точка является критической).
Понятие критической точки допускает обобщение на случай дифференцируемых отображений 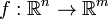 , и на случай дифференцируемых отображений произвольных многообразий
, и на случай дифференцируемых отображений произвольных многообразий 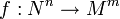 . В этом случае определение критической. точки состоит в том, что ранг матрицы Якоби отображения
. В этом случае определение критической. точки состоит в том, что ранг матрицы Якоби отображения 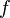 в ней меньший максимального (равного числу
в ней меньший максимального (равного числу 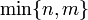 ).
).
Критические точки функций и отображений играют важную роль в таких областях математики, как дифференциальные уравнения, вариационное исчисление, теория устойчивости, а также в механике и физике. Исследование критических точек гладких отображений составляет один из главных вопросов теории катастроф.
Понятие критической точки обобщается также на случай функционалов, определенных на бесконечномерных функциональных пространствах. Поиск критических точек таких функционалов является важной частью вариационного исчисления. Критические точки функционалов (которые, в свою очередь, являются функциями) называются экстремалями.
1. Первое достаточное условие экстремума.
Теорема 9.1. Пусть
- точка с является точкой возможного экстремума функции f(x),
- f(x) дифференцируема всюду в некоторой окрестности точки с.
Тогда, если в пределах указанной окрестности слева от точки с и справа от точки с, то функция f(x) имеет в точке с локальный максимум (минимум). Если же f'(x) имеет один и тот же знак слева и справа от точки с, то экстремума в точке с нет.
Доказательство.
1). Пусть слева от точки с и справа от с. Обозначим x0 ≠ c любое значение аргумента из рассматриваемой окрестности. Достаточно доказать, что
Функция f(x) дифференцируема (а следовательно, непрерывна) на сегменте . По формуле Лагранжа (формула конечных приращений)
(1)
где ξ лежит между c и x0. Т.к. при и при , то правая часть (1) положительна (отрицательна).
2). Пусть теперь f'(x) имеет один и тот же знак слева и справа от c. Обозначая через x0 любое значение аргумента, отличное от c, и повторяя проведенные выше рассуждения, мы докажем, что правая часть (1) имеет разные знаки слева и справа от с. Это доказывает отсутствие экстремума в точке с.
Теорема доказана.
Вытекающее из Теоремы 9.1 правило
1). Если при переходе через данную точку с возможного экстремума производная f'(x) меняет знак с плюса на минус (с минуса на плюс), то функция f(x) имеет в точке с локальный максимум (минимум).
2). Если же при переходе через данную точку с возможного экстремума производная f'(x) не меняет знака, то экстремума в точке с нет.
Пример.
, x = 2 - точка возможного экстремума. Т.к. как слева, так и справа от x = 2, то экстремума в этой точке нет.
