Определение граничных значений напряжения и тока
Значения постоянных интегрирования определяются однозначно только после включения отрезка линии в состав электрической цепи и выбираются такими, чтобы при x¢ = 0 соблюдались граничные условия. Рассмотрим процедуру получения и использования граничных условий полубесконечного отрезка линии, подключённого к автономному (активному) сосредоточенному двухполюснику (Рис. 4).
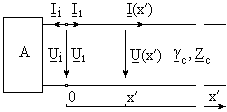 Рис. 4 Рис. 4 |
Запишем сначала выражение комплексной характеристики автономного сосредоточенного двухполюсника, к примеру, в Z-форме
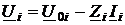
и выражение напряжения U(x¢) в начале отрезка линии (x¢ =0)
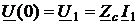 .
.
По Рис. 4 составим условия сопряжения значений напряжений и токов автономного двухполюсника и начала отрезка линии:
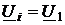 и
и 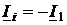 .
.
С учётом последних равенств комплексная характеристика автономного двухполюсника примет вид
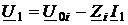 .
.
Это и есть искомое выражение граничного условия полубесконечного отрезка линии; вместе с комплексной характеристикой отрезка в Z-форме (15) оно позволяет найти искомые значения постоянных интегрирования I1и U1:
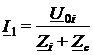 ;
; 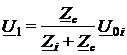 .
.
Этим формулам отвечает схема электрической цепи с сосредоточенными компонентами (Рис. 5), на которой полубесконечный отрезок однородной линии представлен пассивной ветвью сопротивлением Zc. Если же исходить из комплексных характеристик автономного двухполюсника и полубесконечного отрезка однородной линии в Y-параметрах, то, после аналогичных выкладок придём к выражениям, дуальным предыдущим:
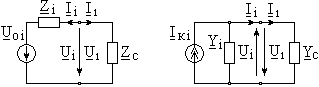 Рис. 5 Рис. 6 Рис. 5 Рис. 6 |
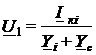 ;
; 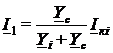 .
.
которым соответствует схема электрической цепи с сосредоточенными компонентами, представленная на Рис. 6. В дальнейшем при определении значений постоянных интегрирования общих решений телеграфных уравнений мы будем пользоваться этими или подобными им схемами, минуя рассмотренную процедуру вывода граничных условий.
Волны напряжения и тока
Перейдём к мгновенным значениям напряжения u(x¢, t) и тока i(x¢, t) в произвольном сечении отрезка с координатой x¢. Полагая в выражении (11) 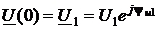 в соответствии, например, с формулами (3), получаем
в соответствии, например, с формулами (3), получаем
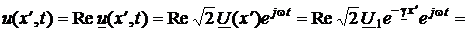
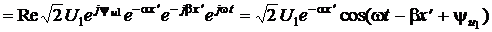 .
.
Отсюда видно, что при фиксированном значении координаты x¢ напряжение u(x¢, t) этого сечения является гармонической функцией времени с частотой w и постоянной амплитудой 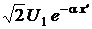 . Если же зафиксировать момент времени t и рассматривать изменение напряжения вдоль полубесконечного отрезка, то получим осциллирующую знакопеременную функцию амплитуда которой
. Если же зафиксировать момент времени t и рассматривать изменение напряжения вдоль полубесконечного отрезка, то получим осциллирующую знакопеременную функцию амплитуда которой 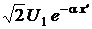 убывает по экспоненте с ростом x¢, то есть по мере удаления от начала отрезка линии.
убывает по экспоненте с ростом x¢, то есть по мере удаления от начала отрезка линии.
С течением времени распределение напряжения перемещается вдоль отрезка линии, образуя волну напряжения. Для определённости, за скорость распространения волны 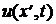 примем её так называемую фазовую скорость vф, под которой понимают скорость перемещения её сечения в выбранной неподвижной системе координат, фаза колебания в котором
примем её так называемую фазовую скорость vф, под которой понимают скорость перемещения её сечения в выбранной неподвижной системе координат, фаза колебания в котором 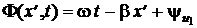 остаётся неизменной. Отсюда видно, что с течением времени t значение фазы волны остаётся неизменным, если значение координаты её сечения x¢ соответствующим образом возрастает. Таким образом, волна напряжения перемещается (бежит) от начала отрезка линии. Из условия постоянства значения фазы бегущей волны
остаётся неизменной. Отсюда видно, что с течением времени t значение фазы волны остаётся неизменным, если значение координаты её сечения x¢ соответствующим образом возрастает. Таким образом, волна напряжения перемещается (бежит) от начала отрезка линии. Из условия постоянства значения фазы бегущей волны 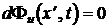 или
или
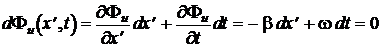
следует, что волна напряжения 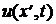 перемещается вдоль отрезка линии с фазовой скоростью
перемещается вдоль отрезка линии с фазовой скоростью
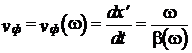
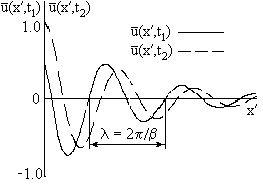 Рис. 7 Рис. 7 |
На Рис. 7 изображены нормированные на амплитуду Um волны напряжения для двух следующим друг за другом моментов времени t1и t2, причём 0 < t2 – t1 < T/2.
Аналогично можно рассмотреть изменения тока вдоль полубесконечного отрезка однородной линии и получить выражение
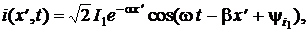
которое описывает волну тока, бегущую от начала отрезка с тем же значением фазовой скорости vф и так же затухающую в направлении своего распространения.
Из выражений волн напряжения 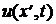 и тока
и тока 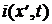 следует, что значение коэффициента затухания
следует, что значение коэффициента затухания 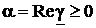 , входящего в показатель экспоненты, характеризует убывание амплитуд волн при их распространении вдоль отрезка линии. Фазы напряжения и тока изменяются вдоль отрезка линии по линейному закону. Коэффициент фазы b определяет скорость этих изменений. Разность фаз напряжения и тока в любом сечении отрезка равен аргументу характеристического сопротивления линии
, входящего в показатель экспоненты, характеризует убывание амплитуд волн при их распространении вдоль отрезка линии. Фазы напряжения и тока изменяются вдоль отрезка линии по линейному закону. Коэффициент фазы b определяет скорость этих изменений. Разность фаз напряжения и тока в любом сечении отрезка равен аргументу характеристического сопротивления линии
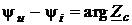 .
.
Коэффициент затухания a выражается в неперах или децибелах на единицу длины, а коэффициент фазы b – в радианах на единицу длины.
Убывание амплитуд волн напряжения и тока в направлении их перемещения обусловливается необратимыми преобразованиями энергии вдоль отрезка линии, а изменение их фаз – конечными значениями фазовых скоростей распространения этих волн.
