Сходимость числового ряда. сумма ряда
Глава 8. Числовые ряды
Основные понятия
Определение числового ряда
Множество чисел перенумерованных с помощью натуральных чисел и расставленных в порядке возрастания их номеров называется числовой последовательностью
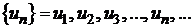 .
.
Числовым рядом называется сумма членов бесконечной числовой последовательности
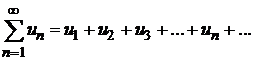 .
.
Ряд считается заданным, если известен закон образования n-го (общего) члена ряда в зависимости от его номера. Обычно общий член ряда задается как функция 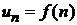 или
или 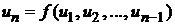 .
.
Например: 1) если 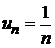 , то
, то 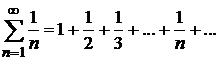 ;
;
2) если 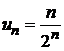 , то
, то 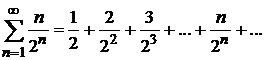 ;
;
3) если 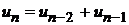 ,
, 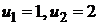 , то
, то
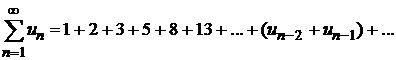 .
.
Обычно, при исследовании числовых рядов возникает необходимость нахождения вида общего члена ряда как функции от номера этого члена. Для этого нужно перенумеровать члены ряда и, учитывая четность, периодичность и другие особенности его членов записать функцию 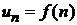 .
.
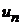 | 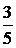 + + | 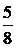 + + | 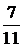 + + | …. + | 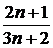 + … + … |
| n | ××× | n |
Например: 1)
Числитель каждого следующего члена этого ряда на 2 больше, а знаменатель на 3 больше, поэтому в n-ом члене ряда нужно записать в числителе 2n , а в знаменателе 3n.Кроме того, в числителе нужно к 2n прибавить 1, а в знаменателе к 3n прибавить 2, чтобы при n = 1 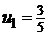 . Тогда
. Тогда 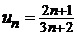 .
.
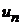 | 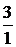 + + | 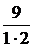 + + | 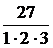 + + | …. + | 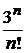 + … + … |
| n | ××× | n |
2)
Числители являются степенями числа 3, а в знаменателях находится факториалы номеров членов n, 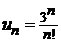 .
.
Сходимость числового ряда. Сумма ряда
В прикладных задачах, как правило, требуется найти сумму ряда. Ряд представляет собой бесконечную сумму, поэтому найти точное значение суммы ряда, обычно, не представляется возможным. Однако сумму ряда можно найти приближенно, если есть уверенность, что она существует. Дело в том, что сумма ряда даже с очень малыми членами может быть бесконечно большой или вообще не существовать. Поэтому основная трудность при нахождении суммы ряда заключается в том, чтобы доказать, что она существует.
Числовой ряд разделяют на две части
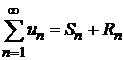 .
.
Сумма первых n членов ряданазывается n-ой частичной суммой ряда
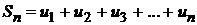 .
.
Сумма всех членов ряда, начиная с(n+1)-го, называется n-ым остатком ряда
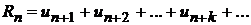 .
.
Ряд называется сходящимся, если существует предел 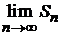 последовательности n-ых частичных сумм ряда
последовательности n-ых частичных сумм ряда 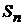
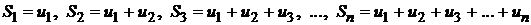 .
.
Если предел частичных сумм 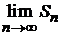 не существует, ряд называетсярасходящимся.
не существует, ряд называетсярасходящимся.
Если ряд сходится, то предел частичных сумм ряда называется суммой ряда, т. е. 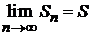 .
.
Пример 8.1. Исследовать сходимость ряда, являющегося геометрической прогрессией
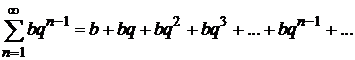 ,
,
где b - первый член прогрессии, q - знаменатель прогрессии.
Известно, что n -я частичная сумма этого ряда равняется
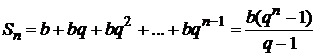 .
.
В зависимости от величины знаменателя прогрессии q возможны 4 случая.
1. Если 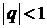 , то
, то 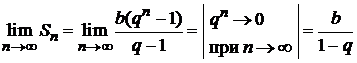
является конечной величиной и, следовательно, ряд сходится.
2. Если 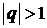 , то
, то 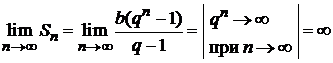
является бесконечно большой величиной и, следовательно, ряд расходится.
3. Если 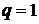 , то
, то 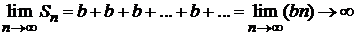
является бесконечно большой величиной и, следовательно, ряд расходится.
4. Если 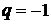 , то
, то
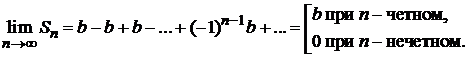
Следовательно, предел 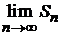 не существует и ряд расходится.
не существует и ряд расходится.
Свойства сходящихся рядов
1. Сходимость числового ряда 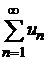 не нарушится, если все его члены умножить на некоторое отличное от нуля число l; причем
не нарушится, если все его члены умножить на некоторое отличное от нуля число l; причем
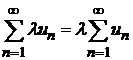 .
.
Д о к а з а т е л ь с т в о. Используем определение суммы ряда и свойства пределов, получаем
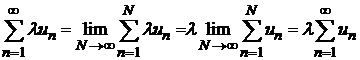 .
.
2. При сложении соответствующих членов двух сходящихся рядов 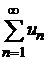 и
и 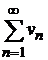 получится сходящийся ряд; причем
получится сходящийся ряд; причем
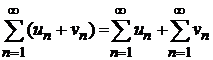 .
.
Д о к а з а т е л ь с т в о. Используем определение суммы ряда и свойства пределов, получаем
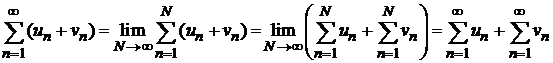 .
.
3. Сходимость ряда не нарушится, если отбросить конечное число его членов.
Д о к а з а т е л ь с т в о. Пусть сумма ряда 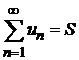 . Не нарушая общности можно считать, что отбрасываются k первых его членов, сумма которых
. Не нарушая общности можно считать, что отбрасываются k первых его членов, сумма которых 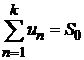 . Так как ряд сходящийся, то
. Так как ряд сходящийся, то 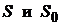 являются конечными величинами, поэтому
являются конечными величинами, поэтому 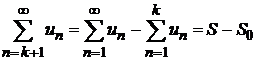 так же является конечной величиной и, следовательно, ряд
так же является конечной величиной и, следовательно, ряд 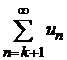 сходится.
сходится.
Отсюда также следует, что если в расходящемся ряде отбросить конечное число членов, то ряд останется расходящимся.
Числовых рядов
Признаки сравнения рядов
Теорема 8.2(Первый признак сравнения рядов).
1. Если члены знакоположительного ряда 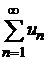 не превосходят соответствующих членов сходящегося ряда
не превосходят соответствующих членов сходящегося ряда 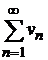 , т. е.
, т. е. 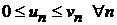 , то он сходится.
, то он сходится.
2. Если члены знакоположительного ряда 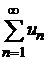 не меньше соответствующих членов расходящегося ряда
не меньше соответствующих членов расходящегося ряда 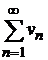 , т. е.
, т. е. 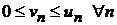 , то он расходится.
, то он расходится.
Д о к а з а т е л ь с т в о. Докажем первое утверждение теоремы. Пусть ряд 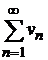 сходится и его сумма равна
сходится и его сумма равна 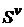 .
.
Ряд 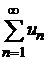 знакоположительный, поэтому последовательность его n-ых частичных сумм
знакоположительный, поэтому последовательность его n-ых частичных сумм 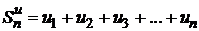 монотонно возрастает при увеличении n.
монотонно возрастает при увеличении n.
Члены ряда 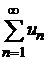 не превосходят соответствующих членов ряда
не превосходят соответствующих членов ряда 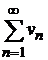 , т. е.
, т. е. 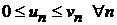 . Ввиду этого частичные суммы рядов удовлетворяют неравенству
. Ввиду этого частичные суммы рядов удовлетворяют неравенству
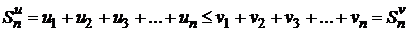 .
.
Кроме того, очевидно, что 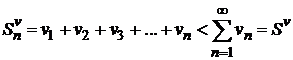 . Следовательно, последовательность частичных сумм
. Следовательно, последовательность частичных сумм 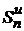 монотонно возрастает и ограничена (
монотонно возрастает и ограничена ( 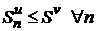 ). По теореме Вейерштрасса эта последовательность имеет предел
). По теореме Вейерштрасса эта последовательность имеет предел 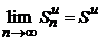 . Ряд
. Ряд 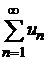 сходится.
сходится.
Второе утверждение теоремы докажем от противного. Пусть известно, что ряд 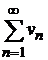 расходится и
расходится и 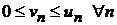 . Предположим, что ряд
. Предположим, что ряд 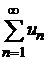 сходится. Тогда по первому утверждению данной теоремы должен сходиться также ряд
сходится. Тогда по первому утверждению данной теоремы должен сходиться также ряд 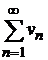 . В этом и состоит противоречие.
. В этом и состоит противоречие.
Пример 8.4. Исследовать сходимость ряда 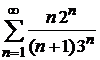 .
.
Для сравнения выберем сходящийся ряд, являющийся бесконечной убывающей геометрической прогрессией 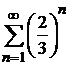 , которая сходится, так как знаменатель прогрессии
, которая сходится, так как знаменатель прогрессии 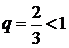 . Члены исследуемого ряда не превосходят соответствующих членов предложенной геометрической прогрессии
. Члены исследуемого ряда не превосходят соответствующих членов предложенной геометрической прогрессии 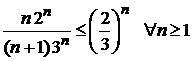 . В соответствии с пунктом 1 теоремы 8.2 ряд сходится.
. В соответствии с пунктом 1 теоремы 8.2 ряд сходится.
Пример 8.5. Исследовать сходимость ряда 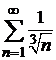 .
.
Для сравнения выберем расходящийся гармонический ряд 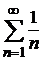 . Члены исследуемого ряда больше соответствующих членов гармонического ряда
. Члены исследуемого ряда больше соответствующих членов гармонического ряда 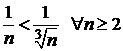 , поэтому ряд также расходится.
, поэтому ряд также расходится.
Теорема 8.3 (Второй признак сравнения рядов). Если отличен от нуля конечный предел отношения соответствующих членов двух знакоположительных рядов 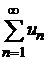 и
и 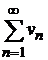 , т. е.
, т. е. 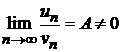 , то данные ряды сходятся или расходятся одновременно.
, то данные ряды сходятся или расходятся одновременно.
Д о к а з т е л ь с т в о. По определению предела по Коши на языке e-d существование предела отношения членов рядов означает:
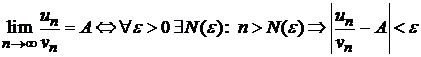 .
.
Это значит, что для любого n > N(e) справедливы неравенства
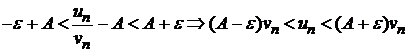 .
.
Сходимость рядов не зависит от того, что будет отброшено конечное число членов (N(e)). Члены рядов можно перенумеровать и считать, что последнее неравенство выполняется, начиная с n =1. т. е.
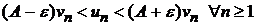 .
.
Тогда для частичных сумм рядов можно записать
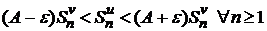 , где
, где 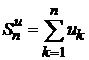 ,
, 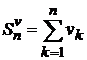 .
.
Далее рассмотрим два случая.
1. Ряд 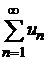 сходится. Тогда предел его частичных сумм существует и является конечной величиной
сходится. Тогда предел его частичных сумм существует и является конечной величиной 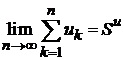 . Учитывая это и левую часть последнего неравенства
. Учитывая это и левую часть последнего неравенства 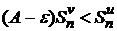 , можно записать
, можно записать 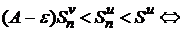
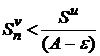 , т. е. последовательность частичных сумм ряда
, т. е. последовательность частичных сумм ряда 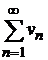 , являющаяся монотонно возрастающей, ограничена. По теореме Вейерштрасса она имеет предел и, следовательно, ряд сходится.
, являющаяся монотонно возрастающей, ограничена. По теореме Вейерштрасса она имеет предел и, следовательно, ряд сходится.
2. Ряд 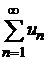 расходится, т. е.
расходится, т. е. 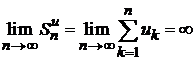 . Тогда, учитывая правую часть выше полученного неравенства, имеем
. Тогда, учитывая правую часть выше полученного неравенства, имеем 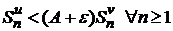 . Отсюда можно сделать вывод, что предел частичных сумм второго ряда также неограничен
. Отсюда можно сделать вывод, что предел частичных сумм второго ряда также неограничен 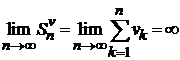 . Следовательно, ряд
. Следовательно, ряд 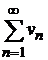 расходится.
расходится.
Можно аналогично рассуждать, начиная с предположений о сходимости ряда 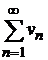 , показать, что одновременно с ним сходится или расходится ряд
, показать, что одновременно с ним сходится или расходится ряд 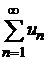 .
.
Пример 8.6. Исследовать сходимость ряда 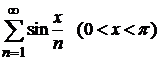 .
.
Сравним исходный ряд с гармоническим рядом 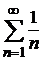 . Используем первый замечательный предел, находим
. Используем первый замечательный предел, находим
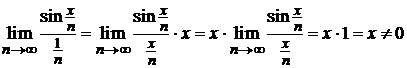 .
.
Отсюда следует, что исследуемый ряд расходится так же, как и гармонический.
Теорема 8.4. (Третий признак сравнения рядов).
1. Если отношение последующего члена ряда к предыдущему для ряда 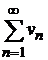 не превосходит соответствующего отношения последующего члена ряда к предыдущему для сходящегося ряда
не превосходит соответствующего отношения последующего члена ряда к предыдущему для сходящегося ряда 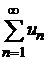 , т. е.
, т. е. 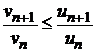 для любого n, то ряд
для любого n, то ряд 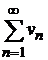 сходится.
сходится.
2. Если же 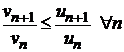 и ряд
и ряд 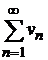 расходится, то и ряд
расходится, то и ряд 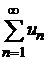 расходится.
расходится.
Д о к а з а т е л ь с т в о. По условию теоремы для любого n имеют место неравенства
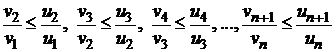 .
.
Перемножим почленно левые и правые части этих неравенств, получим
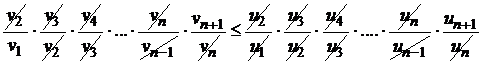 .
.
Сократим одинаковые члены в числителях и знаменателях левой и правой частях неравенства, получим
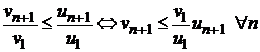 .
.
Отсюда следует, если ряд 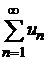 сходится, то по теореме 8.2 сравнения рядов также сходится ряд
сходится, то по теореме 8.2 сравнения рядов также сходится ряд 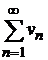 , так как его члены не превосходят соответствующих членов сходящегося ряда
, так как его члены не превосходят соответствующих членов сходящегося ряда 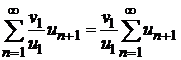 . На основании той же теоремы, если ряд
. На основании той же теоремы, если ряд 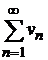 расходится, то и ряд
расходится, то и ряд 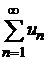 расходится.
расходится.
Интегральный признак Коши
Теорема 8.6. Если члены знакоположительного ряда 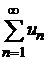 , являющиеся значениями функции целочисленного аргумента
, являющиеся значениями функции целочисленного аргумента 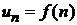 , монотонно убывают и стремятся к нулю
, монотонно убывают и стремятся к нулю 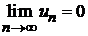 , то: 1) если
, то: 1) если 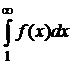 сходится, то и ряд
сходится, то и ряд 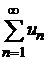 сходится; 2) если
сходится; 2) если 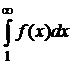 расходится, то и ряд
расходится, то и ряд 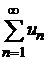 расходится.
расходится.
Д о к о з а т е л ь с т в о. В прямоугольной декартовой системе координат  непрерывная кривая
непрерывная кривая 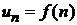 проходит через точки
проходит через точки 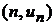 и ограничивает сверху криволинейную трапецию ABCD (рис. 86). Площадь этой криволинейной трапеции равняется
и ограничивает сверху криволинейную трапецию ABCD (рис. 86). Площадь этой криволинейной трапеции равняется 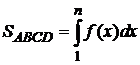 .
.
Построим две ступенчатые фигуры с угловыми точками 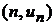
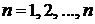 . Эти ступенчатые фигуры состоят из прямоугольников, основания которых равняются единице, а высоты значениям
. Эти ступенчатые фигуры состоят из прямоугольников, основания которых равняются единице, а высоты значениям 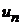 .
.
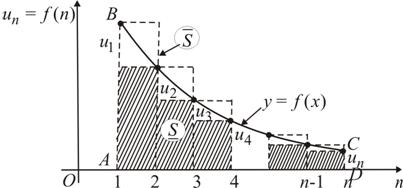
Рис. 86
Найдем площади этих фигур.
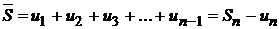 ,
,
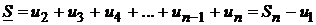 ,
,
где 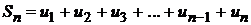 - n-я частичная сумма ряда.
- n-я частичная сумма ряда.
Площади этих ступенчатых фигур ограничивают площадь криволинейной трапеции ABCD снизу и сверху
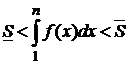 Û
Û 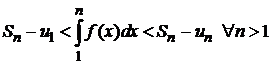 .
.
Рассмотрим левую часть этого неравенства
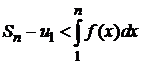 Û
Û 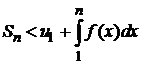 .
.
При неограниченном возрастании числа n членов ряда частичные суммы ряда монотонно возрастают, так как ряд знакоположительный. При этом интеграл 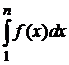 также возрастает и ограничен величиной интеграла
также возрастает и ограничен величиной интеграла 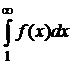 . Поэтому
. Поэтому 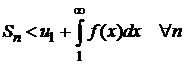 , т. е. последовательность частичных сумм ограничена. По теореме Вейерштрасса существует предел
, т. е. последовательность частичных сумм ограничена. По теореме Вейерштрасса существует предел 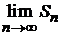 . Следовательно, ряд сходится.
. Следовательно, ряд сходится.
Рассмотрим правую часть неравенства
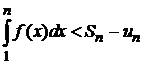 Û
Û 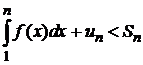 .
.
По условию теоремы 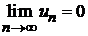 .
.
Если 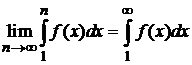 неограниченно возрастает, то и предел частичных сумм
неограниченно возрастает, то и предел частичных сумм 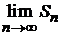 неограниченно возрастает и, следовательно, ряд расходится.
неограниченно возрастает и, следовательно, ряд расходится.
Таким образом, интегральный признак Коши в принципе позволяет для любого ряда решить вопрос о его сходимости. Трудность в его применении заключается в нахождении несобственных интегралов. Возможности в их нахождении ограниченные.
Пример 8.13. Исследовать гармонического сходимость ряда 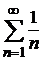 .
.
Находим 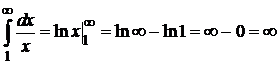 . Ряд расходится.
. Ряд расходится.
Пример 8.14. Исследовать сходимость обобщенного гармонического ряда 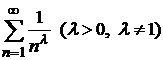 .
.
Находим 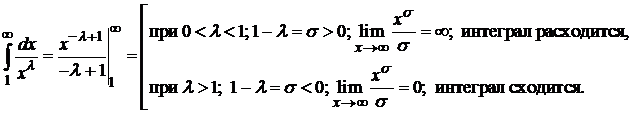
Следовательно, при 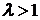 ряд сходится, а при
ряд сходится, а при 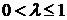 ряд расходится.
ряд расходится.
Пример 8.15. Исследовать сходимость ряда 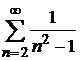 .
.
Члены ряда нумеруются с 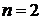 (при
(при 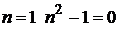 ). Поэтому при применении интегрального признака Коши нижний предел интегрирования равен 2, а не 1. Находим
). Поэтому при применении интегрального признака Коши нижний предел интегрирования равен 2, а не 1. Находим
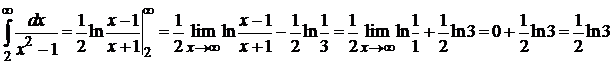 .
.
Здесь при нахождении предела применили правило Лопиталя. Интеграл сходится, следовательно, и ряд сходится.
Пример 8.16. Исследовать сходимость ряда 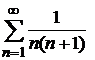 .
.
Находим
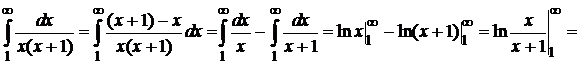
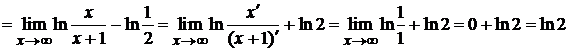 .
.
Ряд сходится.
Числового ряда
Теорема 8.8.Числовой ряд 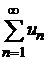 сходится, если сходится ряд, составленный из абсолютных величин его членов
сходится, если сходится ряд, составленный из абсолютных величин его членов 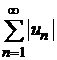 .
.
Д о к а з а т е л ь с т в о. Пусть ряд 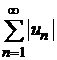 сходится. Тогда по свойству 1 сходящихся рядов также сходится ряд
сходится. Тогда по свойству 1 сходящихся рядов также сходится ряд 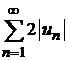 .
.
Так как 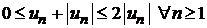 , то по первому признаку сравнения рядов (теорема 8.2) также сходится ряд
, то по первому признаку сравнения рядов (теорема 8.2) также сходится ряд 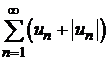 . На основании свойства 2 сходящихся рядов сходится разность двух рядов
. На основании свойства 2 сходящихся рядов сходится разность двух рядов
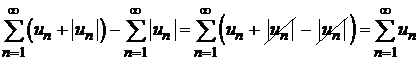 , т. е. исходный ряд.
, т. е. исходный ряд.
Ряд называется абсолютно сходящимся, если он сходится и сходится ряд, составленный из абсолютных величин его членов.
Ряд называется условно сходящимся, если он сходится, а ряд, составленный из абсолютных величин его членов, расходится.
Пример 8.19. Исследовать сходимость ряда 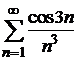 .
.
Так как 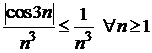 и ряд
и ряд 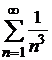 сходится как обобщенно гармонический ряд
сходится как обобщенно гармонический ряд 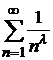 при
при 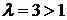 , то по теореме 8.2 сравнения рядов сходится ряд
, то по теореме 8.2 сравнения рядов сходится ряд 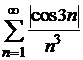 , а по теореме об абсолютной сходимости сходится также ряд
, а по теореме об абсолютной сходимости сходится также ряд 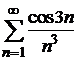 . Следовательно, исходный ряд сходится; причем абсолютно.
. Следовательно, исходный ряд сходится; причем абсолютно.
Пример 8.20. Исследовать на абсолютную сходимость ряд 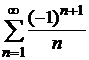 .
.
Ранее было показано, что данный знакочередующийся ряд сходится (пример 8.15). Ряд, составленный из абсолютных величин данного ряда, является гармоническим, который, как известно, расходится. Это означает, что исходный ряд сходится условно.
Глава 9. Степенные ряды
Теорема Вейерштрасса
Функциональный ряд 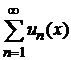 называется равномерно сходящимся к сумме
называется равномерно сходящимся к сумме 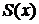 в области G, если при сколь угодно малом значении
в области G, если при сколь угодно малом значении 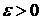 существует такое число
существует такое число 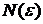 , что если
, что если 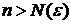 , то для любого х из области сходимости ряда G (
, то для любого х из области сходимости ряда G ( 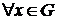 )
)
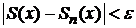 .
.
Теорема 9.1. (Теорема Вейерштрасса о равномерной сходимости ряда).
Если члены функционального ряда 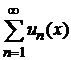 на отрезке
на отрезке 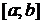 не превосходят по абсолютной величине соответствующих членов знакоположительного сходящегося числового ряда
не превосходят по абсолютной величине соответствующих членов знакоположительного сходящегося числового ряда 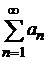 , т. е.
, т. е. 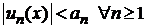 , то ряд сходится абсолютно и равномерно при
, то ряд сходится абсолютно и равномерно при 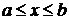 .
.
Равномерно сходящиеся ряды обладают рядом важных свойств.
Свойство 1. Если члены ряда 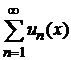 определены и непрерывны на отрезке
определены и непрерывны на отрезке 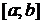 и ряд сходится равномерно к сумме
и ряд сходится равномерно к сумме 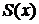 , то эта сумма является непрерывной функцией на этом отрезке.
, то эта сумма является непрерывной функцией на этом отрезке.
Свойство 2. Если члены ряда 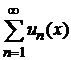 являются непрерывными функциями на отрезке
являются непрерывными функциями на отрезке 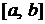 и ряд сходится равномерно к сумме
и ряд сходится равномерно к сумме 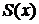 , то его можно почленно интегрировать; причем ряд составленный из интегралов его членов равномерно сходится к интегралу суммы ряда, т. е.
, то его можно почленно интегрировать; причем ряд составленный из интегралов его членов равномерно сходится к интегралу суммы ряда, т. е.
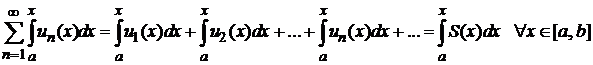 .
.
Свойство 3. Если члены ряда 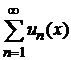 являются непрерывными функциями на интервале
являются непрерывными функциями на интервале 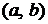 , имеют непрерывные производные
, имеют непрерывные производные 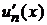 на этом интервале и ряд сходится равномерно к сумме
на этом интервале и ряд сходится равномерно к сумме 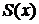 , то его можно почленно дифференцировать; причем ряд составленный из производных его членов равномерно сходится к производной суммы ряда, т. е.
, то его можно почленно дифференцировать; причем ряд составленный из производных его членов равномерно сходится к производной суммы ряда, т. е.
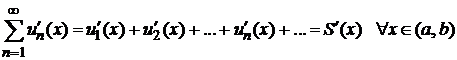 .
.
Ряды Тейлора и Маклорена
Функция 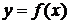 разлагается в степенной ряд
разлагается в степенной ряд 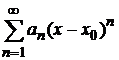 в области G, если он составлен для этой функции и сходится к ней.
в области G, если он составлен для этой функции и сходится к ней.
Пусть степенной ряд
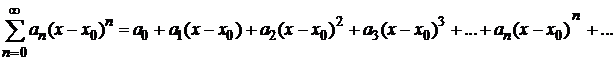
Равномерно сходится к функции 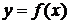 , т. е.
, т. е.
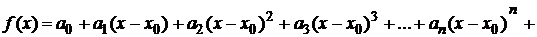
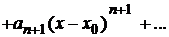
Тогда его можно почленно дифференцировать.
Найдем производные этого ряда.
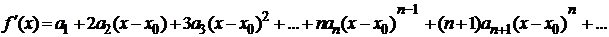 ;
;
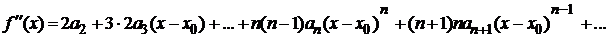 ;
;
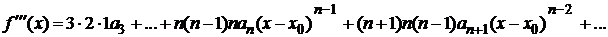 ;
;
………………………………………………………………………………………
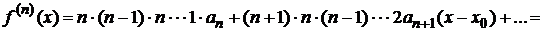
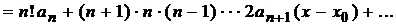
……………………………………………………………………………………………………
Подставим значение 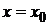 в эти соотношения
в эти соотношения
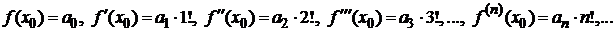 ,получим формулы для нахождения коэффициентов
,получим формулы для нахождения коэффициентов 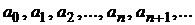
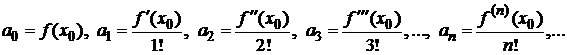
Следовательно,
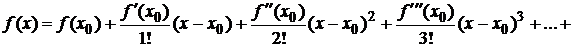
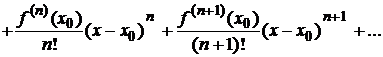
Данный ряд называется рядом Тейлора.
При 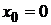 данный ряд имеет вид
данный ряд имеет вид
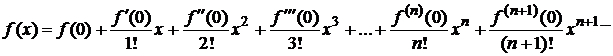
и называется рядом Маклорена.
Разложения функций по данным формулам справедливы только в области сходимости этих рядов.
Ранее были получены формулы Тейлора и Маклорена (Математический анализ. Часть 1. Дифференциальное исчисление).
В формуле Тейлора
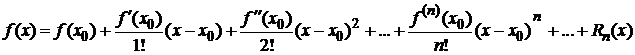
остаточный член 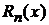 можно рассматривать как остаточный член ряда Тейлора. В форме Лагранжа он имеет вид
можно рассматривать как остаточный член ряда Тейлора. В форме Лагранжа он имеет вид
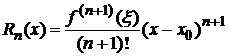 ,
,
где 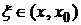 или
или 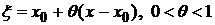 .
.
Также для ряда Маклорена
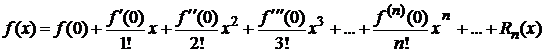
остаточный член в форме Лагранжа имеет вид
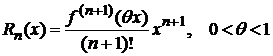 .
.
Теорема 9.2. Для того чтобы степенной ряд 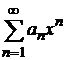 сходился к функции
сходился к функции 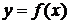 , для которой он составлен, необходимо и достаточно, чтобы остаточный член ряда стремился к нулю при неограниченном увеличении его номера n, т. е.
, для которой он составлен, необходимо и достаточно, чтобы остаточный член ряда стремился к нулю при неограниченном увеличении его номера n, т. е. 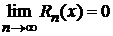 .
.
Д о к а з а т е л ь с т в о.
Необходимость. Пусть ряд 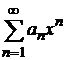 сходится к функции
сходится к функции 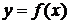 , т. е.
, т. е.
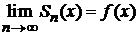 .
.
Так как 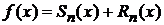 , то
, то
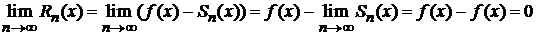 .
.
Достаточность. Пусть 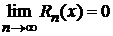 .
.
Тогда
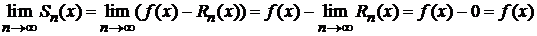 ,
,
т. е. ряд сходится.
Вопросы к экзамену
Неопределённый интеграл
56. Теорема о существовании первообразной функции.
57. Определение неопределённого интеграла, его свойства, геометрический смысл. Таблица неопределённых интегралов.
58.Методы нахождения неопределённых интегралов. Непосредственное интегрирование. Метод замены переменной.
59.Интегрирование некоторых функций, содержащих квадратный трёхчлен в знаменателе.
60. Интегрирование неопределённых интегралов по частям.
61. Интегрирование дробно-рациональных функций. Разложение на простые дроби.
62. Интегрирование иррациональных функций.
63. Интегрирование тригонометрических функций.
64. Интегрирование иррациональных функций с помощью тригонометрических подстановок. О выражении интегралов через элементарные функции.
Определённый интеграл
65. Задачи, приводящие к понятию определённого интеграла.
66.Верхняя и нижняяинтегральные суммы, их свойства.
67.Определение определённого интеграла. Взаимосвязь неопределённого и определённого интегралов. Формула Ньютона-Лейбница. Свойства определённого интеграла.
68.Методы интегрирования определённых интегралов. Интеграл вида 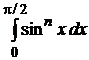 .
.
69.Несобственные интегралы с бесконечными пределами. Теоремы об их сходимости.
70.Несобственные интегралы от разрывных функций. Теоремы об их сходимости.
71. Геометрические приложения определённых интегралов. Вычисление площадей фигур и объёмов тел вращения.
72. Геометрические приложения определённых интегралов. Вычисление длины дуги.
73. Численные методы вычисления определённых интегралов. Формулы прямоугольников и трапеций.
74.Формула Симпсона для вычисления определённых интегралов.
75. Двойные интегралы, их геометрический смысл, свойства.
76.Вычисление двойных интегралов. Перестановка пределов интегрирования.
Дифференциальные уравнения
78.Дифференциальные уравнения. Основные понятия. Нахождение уравнения по его решению.
79. Дифференциальное уравнения первого порядка, его геометрический смысл. Задача Коши. Теорема о существовании и единственности решения.
80. Дифференциальные уравнения с разделяющимися переменными и с однородными функциями.
81. Линейные дифференциальные уравнения, решение методом замены переменной и методом вариации произвольной постоянной.
82. Уравнение Бернулли, его решение.
83. Дифференциальные уравнения высших порядков. Теорема о существовании и единственности решения. Уравнения вида 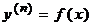 . Уравнения второго порядка, приводимые к уравнениям первого порядка.
. Уравнения второго порядка, приводимые к уравнениям первого порядка.
84. Линейные дифференциальные уравнения n-го порядка, свойства их решений. Определитель Вронского. Общее решение неоднородного уравнения.
85.Комплексные числа, действия над ними.
86. Показательная функция с комплексным показателем, её свойства. Формула Эйлера. Показательная форма комплексного числа.
87. Линейные дифференциальные уравнения n-го порядка с постоянными коэффициентами. Характеристическое уравнение. Вид общего решения однородного уравнения.
88. Нахождение частного решения неоднородного дифференциального уравнения n-го порядка с постоянными коэффициентами.
89. Метод Эйлера численного интегрирования дифференциальных уравнений.
Ряды
90. Числовые ряды, общие понятия, свойства. Необходимый признак сходимости.
91. Признак сравнения знакоположительных рядов (теорема I).
92. Признаки сравнения знакоположительных рядов (теоремы II, III).
93. Признак Даламбера сходимости знакоположительных рядов.
94. Радикальный признак Коши сходимости знакоположительных рядов.
95. Интегральный признак Коши сходимости знакоположительных рядов.
96. Знакочередующиеся ряды. Теорема Лейбница.
97.Знакопеременные ряды. Теорема об абсолютной сходимости числового ряда.
98. Функциональные ряды. Равномерная сходимость, признак Вейерштрасса. Свойства равномерно сходящихся рядов.
99. Степенные ряды. Теорема Абеля о виде области сходимости степенного ряда.
100. Радиус сходимости степенного ряда.
101. Необходимые и достаточные условия разложения функции в степенной ряд. Ряды Тейлора и Маклорена.
102. Разложение основных элементарных функций в степенной ряд Маклорена.
103.Применение рядов для приближенных вычислений.
Экзамен
Литература
Основная литература
1. Общий курс высшей математики для экономистов под ред. В.И.Ермакова. – М.: «ИНФРА-М», 1999.
2. Шипачёв В.С. Высшая математика.–М.: Высшая школа, 1985.
3. Сборник задач по высшей математике для экономистов под ред.В.И.Ермакова. – М.: «ИНФРА-М», 2001.
4. Шершнев В. Г., Сагитов Р. В., Силаева Е. А., Полякова С.Т.
Сборник задач по математическому анализу. – М.: Менеджер, 2008.
Дополнительная литература
1. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике. – М., «ДИС», 1997.
2. Красс М.С. Математика для экономических специальностей. Учебник. –М., Инфра-М, 1998.
3. Красс М.С., Чупрынов Б.П. Основы математики и ее приложения в экономическом образовании. – М., «Дело» , 2000.
4. Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. –М.: Наука. 1989.
5.Минорский В.П. Сборник задач по высшей математике – М.: Наука.
6. Пискунов Н.С. Дифференциальное и интегральное исчисления, т.т. I, II. – М.: Наука, 1976.
МАТЕМАТИЧЕСКИЙ АНАЛИЗ
Глава 8. Числовые ряды
Основные понятия
Определение числового ряда
Множество чисел перенумерованных с помощью натуральных чисел и расставленных в порядке возрастания их номеров называется числовой последовательностью
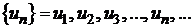 .
.
Числовым рядом называется сумма членов бесконечной числовой последовательности
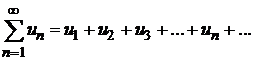 .
.
Ряд считается заданным, если известен закон образования n-го (общего) члена ряда в зависимости от его номера. Обычно общий член ряда задается как функция 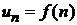 или
или 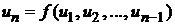 .
.
Например: 1) если 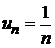 , то
, то 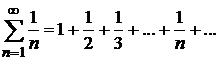 ;
;
2) если 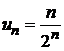 , то
, то 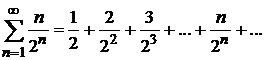 ;
;
3) если 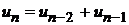 ,
, 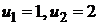 , то
, то
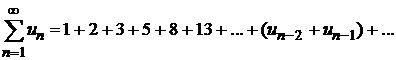 .
.
Обычно, при исследовании числовых рядов возникает необходимость нахождения вида общего члена ряда как функции от номера этого члена. Для этого нужно перенумеровать члены ряда и, учитывая четность, периодичность и другие особенности его членов записать функцию 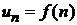 .
.
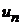 | 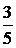 + + | 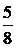 + + | 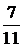 + + | …. + | 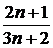 + … + … |
| n | ××× | n |
Например: 1)
Числитель каждого следующего члена этого ряда на 2 больше, а знаменатель на 3 больше, поэтому в n-ом члене ряда нужно записать в числителе 2n , а в знаменателе 3n.Кроме того, в числителе нужно к 2n прибавить 1, а в знаменателе к 3n прибавить 2, чтобы при n = 1 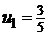 . Тогда
. Тогда 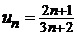 .
.
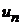 | 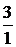 + + | 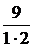 + + | 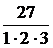 + + | …. + | 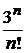 + … + … |
| n | ××× | n |
2)
Числители являются степенями числа 3, а в знаменателях находится факториалы номеров членов n,
