Теоремы о счётных множествах

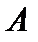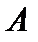Теорема 1. Любое подмножество счётного множества конечно или счётно. Так как множество счётно, то 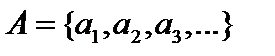. Рассмотрим множество 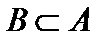. Тогда некоторые из 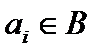, то есть 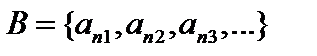. Очевидно, это множество конечно или счётно. ■

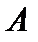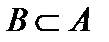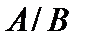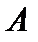Теорема 2 (О минимальности счётного множества). Из любого бесконечного множества можно выделить счётное подмножество так, что множество останется бесконечным. . Так как множество бесконечно, то 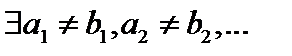и этот процесс не окончится. Таким образом, мы получим счётное множество 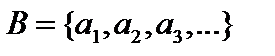и, по крайней мере, счётное множество .■

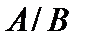Теорема 3 (Об идемпотентности). Объединение 1)конечного числа конечных множеств конечно, 2)счётного числа конечных множеств счётно, 3)конечного числа счётных множеств счётно, 4)счётного числа счётных множеств счётно.

■. Доказательство заключается в указании процедуры пересчёта.

1) выписываем все элементы первого множества, потом все элементы второго, не совпадающие с элементами первого и так далее. 2) 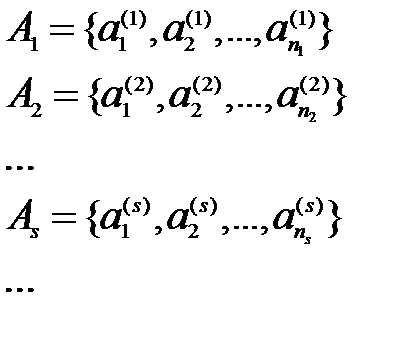Множество 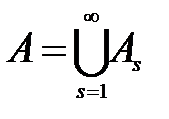строим пересчётом например, по следующей схеме: 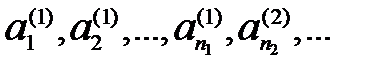, выбрасывая совпадающие элементы.

3) 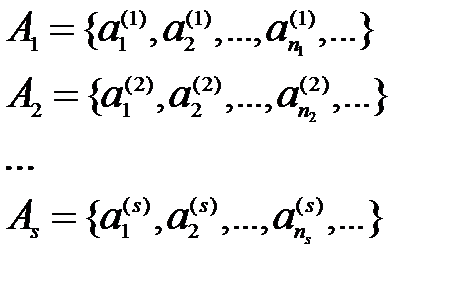Пересчёт

проводим, например, по следующей схеме: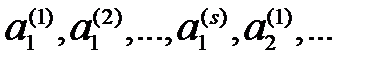

4) 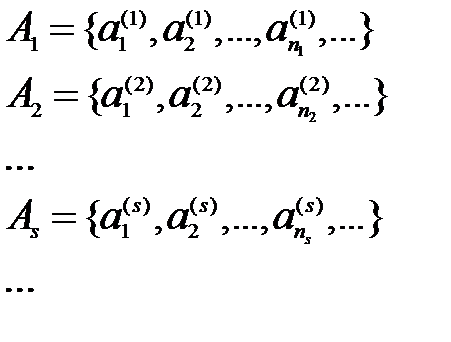. Множество 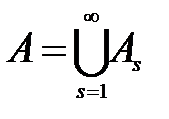строим пересчётом, например, по следующей схеме: 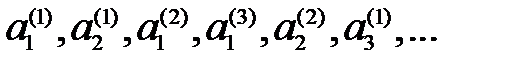, выбрасывая совпадающие элементы. ■

Комментарий. Точно таким же способом пересчёта можно показать счётность множества рациональных чисел, расположив их в виде бесконечной матрицы, выбрасывая совпадающие элементы: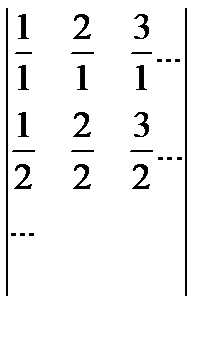

НЕСЧЁТНЫЕ МНОЖЕСТВА

Я возражаю... против употребления актуально

бесконечной величины как чего-либо завершенного,

что никогда не позволительно в математике...

Карл Фридрих Гаусс (1777-1855)

Комментарий. Предыдущие теоремы доказывались установлением биекции между элементами данного множества и элементами множества натуральных чисел. Множество точек отрезка [0, 1] эквивалентно множеству точек отрезка [2,4]; взаимно однозначное соответствие осуществляет, например, функция 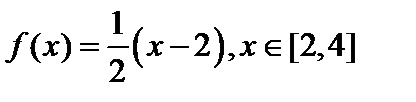. Легко установить биекцию между отрезком 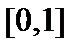и всей числовой осью. Это можно сделать, например, в два этапа. Во-первых, с помощью функции 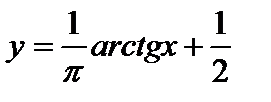устанавливаем биекцию между интервалом 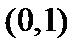и всей числовой осью. Во-вторых, выделим на интервале 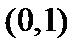какую-нибудь последовательность попарно различных точек, например 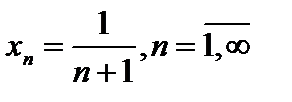. Точке 0 сопоставим точку 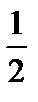, а точке 1 сопоставим точку 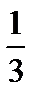. Теперь последовательности 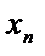биективно сопоставляется последовательность 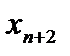, а остальные точки отрезка 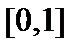и интервала 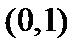соответствуют сами себе. Правило такого сопоставления называется “отелем Гильберта”:

Отель Гильберта.Допустим, что в отеле с бесконечным числом комнат все комнаты заняты и 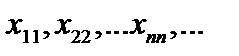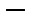список всех постояльцев отеля, где 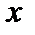с первым индексом 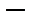имя жильца, а второй индекс 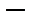номер комнаты. Пусть теперь прибывает новый гость, скажем, 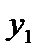. В таком случае метрдотель переселяет постояльца из комнаты 1 в комнату 2, из комнаты 2 - в комнату 3, и т.д. Таким образом метрдотель освобождает комнату 1, поселяет в эту комнату вновь прибывшего гостя и получает новый список всех постояльцев: .

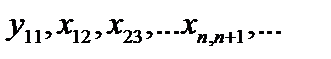Эту биекцию можно провести иначе. Пусть 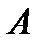– это множество точек интервала 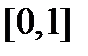, согнутого в виде полуокружности, а 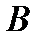– это множество точек числовой оси. Тогда между элементами этих множеств легко установить биекцию. Точка 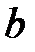–есть пересечение прямой 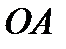с числовой осью. И, наоборот, взяв любую точку 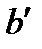из 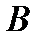и, проведя ту самую прямую 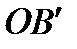, мы получим ту единственную точку 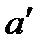, которая поставлена в соответствие с .

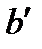0 1 А

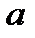
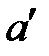
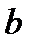
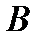
Таким образом, на любом конечном отрезке и на бесконечной прямой, грубо говоря, “одинаковое число точек”. Более того 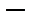можно показать, что на любом конечном отрезке и в любом конечномерном пространстве любой размерности тоже “одинаковое число точек”. Проецирование с центром в точке S устанавливает биекцию между точками 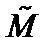сферы и 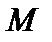плоскости.

a

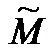М

S

A

B

Это, кстати, подвергает сомнению понимание размерности пространства, как минимальное число параметров, необходимых для описания положения точки в пространстве. Действительно, рассмотрим точку, принадлежащую единичному квадрату с координатами x=0,a₁a₂a₃… и y=0,b₁b₂b₃… в виде десятичных дробей. Здесь a_i и b_i — цифры в десятичной записи дробей. Сопоставим этой точке точку единичного отрезка с координатой z=0,a₁b₁a₂b₂a₃b₃…(кодировка Кантора).

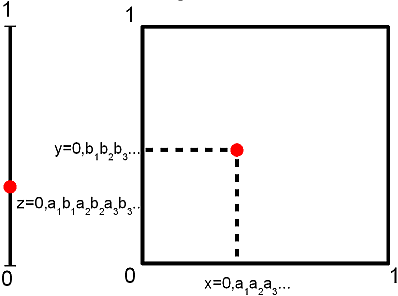
Ясно, что разным точкам единичного квадрата таким отображением сопоставляются разные точки отрезка. При очевидных уточнениях получаем взаимно однозначное отображение квадрата в отрезок. Совершенно аналогично получается взаимно однозначное отображение 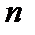-мерного куба в отрезок. Заметим, что существует непрерывное отображение отрезка в квадрат, которое проходит через любую точку квадрата. Оно называется кривой Пеано. Но “количество точек” на отрезке 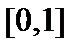не является счётным.

Разумеемся, прямая не состоит из точек, а плоскость из прямых. Речь идёт о размещении точек на прямой, как воробьёв на ветке. Поэтому выражение “количество точек” на отрезке 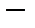это эвфемизм, который следует понимать, как количество точек, которые можно поместить на отрезке.

Теорема (Кантора о несчётности точекотрезка 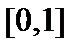). Множество точек отрезка 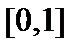не счётно. 1. Диагональная процедура Кантора. 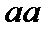. Пустьмножество точек отрезка 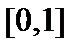счётно, и все они перечислены: 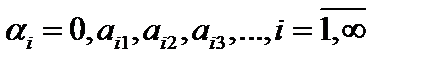. Построим дробь 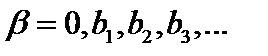так, что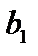 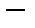любая цифра, не содержащая 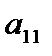, и так далее. Так как существуют числа, которые могут записывается двояко, например 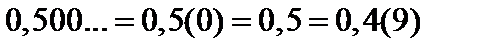, то 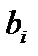не должно содержать цифр 0 и 9. Очевидно, что числа 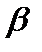нет в списке всех чисел 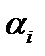отрезка 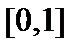, что противоречит условию. ■

. 2. Метод триад Кантора. 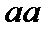. Занумеруем все числа отрезка 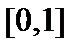: 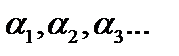, а отрезок 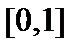разобьём на три части. Это равносильно записи числа в троичной системе счисления. Число 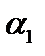не попадёт, по крайней мере, в одну из них. Разобьём её на три части. Число 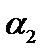не попадёт, по крайней мере, в одну из них. И так далее. В результате получим ССС, то есть существует и единственна точка, принадлежащая всем сегментам сразу. Но её нет в списке всех чисел отрезка 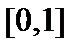по определению. ■

Комментарий. Вспомним начала анализа.

Определение.Если в сегмент 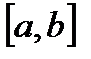вложены сегменты 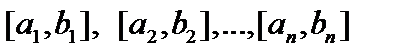так, что 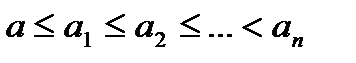, а 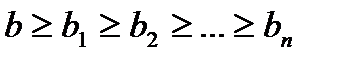, то такая система называется СВС (системой вложенных сегментов).

Определение.Говорят, что 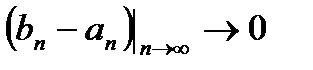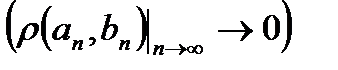(длина сегмента 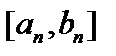стремится к нулю, при условии, что 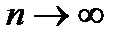), если .

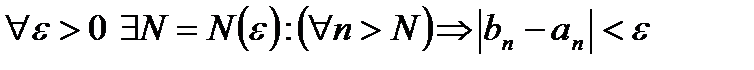Определение.СВС, у которой 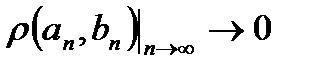называется ССС (системой стягивающих сегментов).

Аксиома Кантора-Дедекинда. В любой СВС существует хоть одна точка, принадлежащая всем им сразу.

Так как рациональные приближения числа 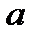можно изобразить системой стягивающихся сегментов, то действительному числу 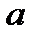будет соответствовать единственная точка числовой оси, если в системе стягивающих сегментов будетединственная точка, принадлежащая всем им сразу (теорема Кантора). Покажем это.

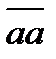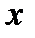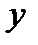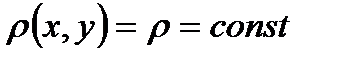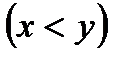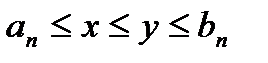■. . Пусть и две такие точки, причём , . Так как, , то 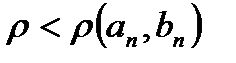. Но, с другой стороны, 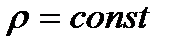, а, т.е. начиная с некоторого номера 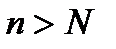, 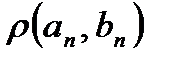будет меньше любой константы. Это противоречие и доказывает требуемое. ■

Биекция между множеством действительных чисел и числовой осью называется полнотой действительной оси.Утверждение, что на действительной оси “нет дырок” фактически постулируется, то есть является предметом математической веры.

Определение. Мощность несчётного множества 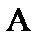точек отрезка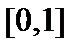 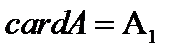называетсямощностью континуума или алеф один.

Примеры. 1. Множество иррациональных чисел несчётно и имеет мощность континуума. Если бы оно было бы счётно, то объединение дух счётных множеств иррациональных и рациональных чисел было бы счётным.

2. Множество всех последовательностей нулей и единиц равномощно множеству всех подмножеств натурального ряда.

■ Сопоставим с каждой последовательностью множество номеров мест, на которых стоят единицы: например, последовательность из одних нулей соответствует пустому множеству, из одних единиц натуральному ряду, а последовательность 10101010... — множеству нечётных чисел. Это множество имеет мощность континуума, так как каждой такой последовательности можно биективно сопоставить дробь 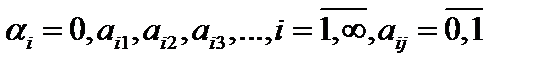, а это двоичное представление действительного числа. То есть множество всех подмножеств натурального ряда, то есть счётного множества, имеет мощность континуума.■

3. Множество бесконечных последовательностей цифр 0, 1, 2, 3

равномощно множеству бесконечных последовательностей цифр 0 и 1, то есть имеет мощность континуума.

■ Закодируем цифры 0, 1, 2, 3 группами 00, 01, 10, 11. Обратное преобразование разбивает последовательность нулей и единиц на пары, после чего каждая пара заменяется на цифру от 0 до 3. ■

4. Множество бесконечных последовательностей цифр
0,1,2 равномощно множеству бесконечных последовательностей цифр 0 и 1, то есть имеет мощность континуума.

■ Закодируем цифры 0, 1 и 2 последовательностями 0, 10 и 11. Теперь всякая последовательность нулей и единиц однозначно разбивается на такие блоки слева направо. ■

5. Доказать, что множество всех бесконечных последовательностей из 0,1,2, в которых 0 и 1 встречаются конечное число раз, счетно.

■ Каждой такой последовательности можно поставить в соответствие бесконечную десятичную дробь вида 0,012120... и т.п. Поскольку в такой дроби только 2 встречается бесконечное число раз, то рано или поздно 2 окажется а периоде, т.е. эта дробь - периодическая. Следовательно множество этих дробей - это множество каких-либо рациональных чисел, т.е. является подмножеством множества рациональных чисел, т.е - счетно. ■

6. Доказать, что множество точек плоскости, лежащих на графике любой функции, заданной на отрезке [0,1], имеет мощность континуума.

■ Множеству таких точек можно поставить в соответствие множество точек отрезка [0,1], которое имеет мощность континуума. ■

Комментарий. Существуют ли множества с мощностью, большей чем 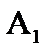? Мы показали, что множество всех подмножеств то есть счётного множества с мощностью 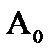имеет мощность континуума 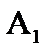. Можно ли построить натуральный ряд алефов?

Пример. Покажем, что множество всех действительных функций, непрерывных и нет, имеет мощность, большую, чем .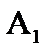

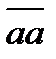■. . Пусть существует биекция между точками действительной оси и всеми действительными функциями, то есть 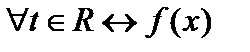. Это фактически означает, что определено множество функций двух переменных 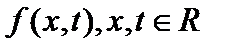. Эти функции определены и при 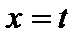, то есть 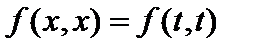. Рассмотрим функцию, отличную от неё, например, функцию 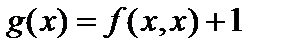. В силу биекции, при каком-то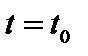 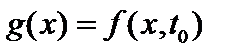. Тогда 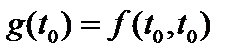. Но 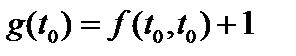. То есть . ■

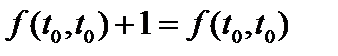Таким образом, множества с мощностью, большей, чем 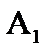существуют. Построить их можно, воспользовавшись следующей теоремой.

Теорема 1(Кантора о больших алефах). Каково бы ни было множество A, множество его подмножеств 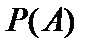имеет большую мощность, то есть 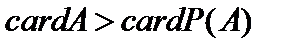. ■. Множество 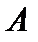эквивалентно части множества 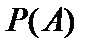, состоящей из одноэлементных подмножеств, то есть 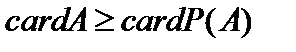. Покажем, что равенство не возможно. 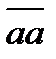. Пусть существует биекция между 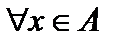и подмножеством 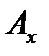множества 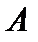. Сам элемент 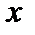может как принадлежать 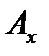, так и нет. Организуем подмножество 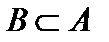тех 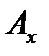, для которых 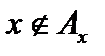, то есть 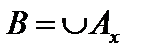. Поскольку существует биекция, то , “представляющее” множество 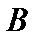, которое может как принадлежать 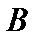, так и нет. Пусть 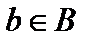. Но в множестве 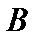собраны все те элементы 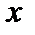, которые не принадлежат своим подмножествам, то есть 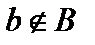. Но если 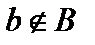, то, так как в множестве 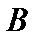собраны все те элементы 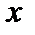, которые не принадлежат своим подмножествам, то 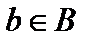. Таким образом, множество 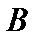не существует и биекция невозможна. ■

Комментарий. Страна состоит из округов, каждый из которых имеет депутата в парламенте. Однако он не обязан жить в своём округе. Президент выделил для депутатов, не живущих в своём округе, отдельный округ и обязал всех их переселиться туда. Очевидно, этот округ должен иметь и своего депутата. Но он не может жить ни в самой этой области, ни вне ее.

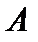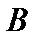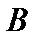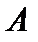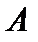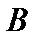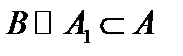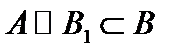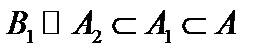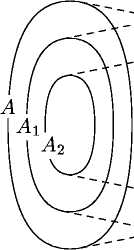
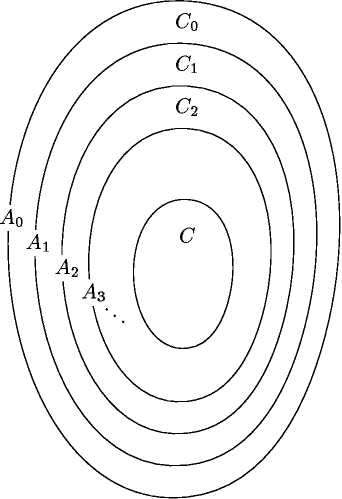
Теорема 2 (Бернштейна об эквивалентности). Пусть множество эквивалентно некоторому подмножеству множества , а множество эквивалентно некоторому подмножеству множества . Тогда бесконечные множества и эквивалентны, то есть . Пусть множества , а множества . При этом множества , то есть 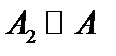. (см. рис.) Другими словам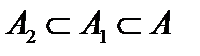и, и 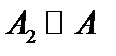. Теперь множество 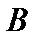уже не нужно и требуется доказать, что 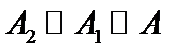. Пусть биекцию между множествам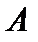и и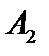

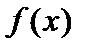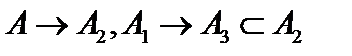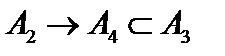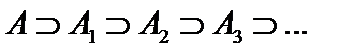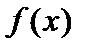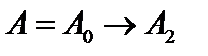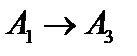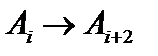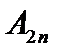
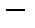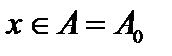
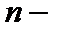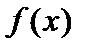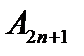
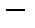обеспечивает функция . Тогда , а и так далее. То есть . Таким образом, функция переводит , , то есть . Фактически это множество тех элементов, которые получаются из любого кратным применением , а это множество тех элементов, которые получаются из любого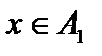 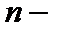кратным применением 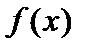. Пересечение всех 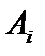может быть пусто, а может быть и нет 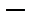это все элементы, у которых сколь угодно много раз можно находить прообраз. Таким образом, множество 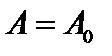разбивается на непересекающиеся слои 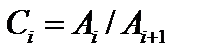и “ядро” 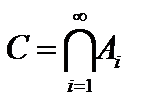, причём слои 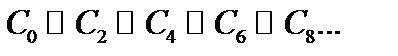, слои 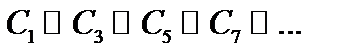, а на “ядре” 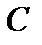функция 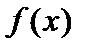всё время переставляет элементы между собой. Теперь ясно, как построить биекцию 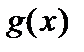между множеством 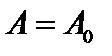и множеством 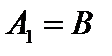. Так как 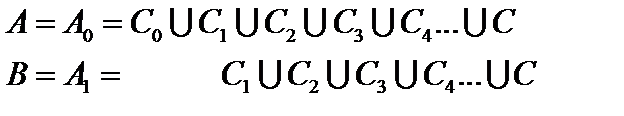, то достаточно

переместить с помощью функции 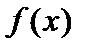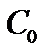на место 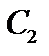, 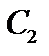на место 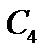и так далее. Опять работает идея “отеля Гильберта”. Теперь очевидно, что бесконечные множества 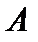и 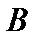эквивалентны. ■

Теперь можно дать определение бесконечному множеству:

Определение (Дедекинд). Множество называют бесконечным, если оно эквивалентно хоть одному собственному подмножеству.

Комментарий. Множества можно рассматривать в двух аспектах: как неупорядоченные и как наделенные некоторым порядком их элементов. Для любых множеств определяется понятие мощности или кардинального числа множества. Для кардинальных чисел (мощностей) строится своя арифметика. Однако чтобы доказывать более тонкие теоремы для бесконечных множеств, понятия множества, лишенного всякой структуры, мало. Для того, чтобы ввести структуру на множестве, его надо арифметизировать, то есть каждому элементу сопоставить некоторую числовую характеристику. Так появляются упорядоченные множества, из которых соответственно и получается обобщение порядковых чисел — трансфинитные ординальныечисла. Каждому ординалу соответствует вполне определенный кардинал, то есть мощность любого вполне упорядоченного множества, которое представляет данный ординал. Сложнее обратное соответствие. Каждое множество определенной мощности можно вполне упорядочить многими способами (бесконечным количеством способов, если оно бесконечно). Поэтому каждому кардиналу соответствует бесконечное множество ординалов, которое Кантор называет числовым классом.

Трансфинитная индукция

Комментарий. Метод математической индукции. Применяется для высказываний 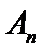, зависящих от натурального параметра 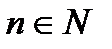. Докажем, что утверждение 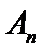справедливо 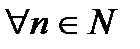, если: 1) Утверждение 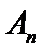справедливо при 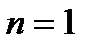и 2) из справедливости 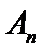для произвольного 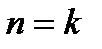следует справедливость его для .

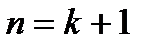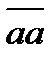■. . Пусть утверждения 1 и 2 выполняются, но 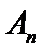справедливо не для всех 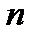. Так как, 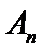справедливо при 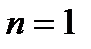(утверждение 1), то существует тако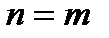е , где 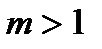, при котором 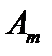не справедливо, причём 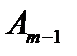ещё справедливо. Положив 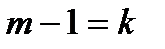, мы получим противоречие с утверждением 2. ■

Для применения метода математической индукции следует сделать следующие операции:

1. Ставится «математический эксперимент», и получают .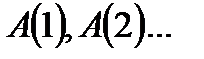

2. Делается предположение о виде формулы 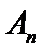. Оно называется “dicto simplisister”, то есть “сказано простаком”.

3. Проверяется утверждение 1 (фактически на первом этапе).

4. Доказывается утверждение 2.

Для натуральных чисел доказательство принципа математической индукции опирается на то, что любое непустое подмножество натуральных чисел имеет наименьший элемент. Если это свойство выполняется для произвольного отношения порядка и произвольного множества, то есть в любом подмножестве рассматриваемого множества есть наименьший элемент относительно рассматриваемого отношения порядка, мы получаем трансфинитную индукцию.

Теорема 1. Пусть есть некоторое вполне упорядоченное множество M и есть некоторая последовательность утверждений 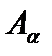, занумерованных элементами 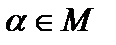. При этом доказываются два утверждения: 1) утверждение 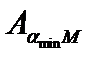истинно; 2) Из того, что для любого 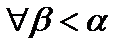все 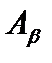истинны, следует, что и 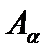истинно. Тогда утверждение 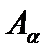истинно .

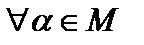Пусть утверждения 1) и 2) выполняются, но среди 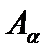есть неверное утверждение. Рассмотрим множество E всех неверных утверждений. Оно непусто, поскольку хотя бы одно утверждение неверно. Возьмем в нем наименьший элемент 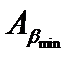, то есть такой элемент, который меньше любого другого элемента множества E (это можно сделать, поскольку 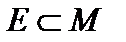, а множество M вполне упорядочено). Тогда для него утверждение 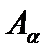неверно, а для предыдущего элемента ещё верно, что противоречит свойству 2). ■