Минимизация на простых множествах

Наиболее простая задача условной минимизации имеет вид

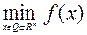, (6.1.1)

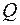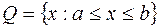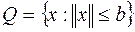где – множество простой структуры. Например, параллелепипед , шар , линейное многообразие .

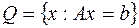Условия экстремума. Точка 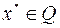называется локальной точкой минимума (или просто точкой минимума) в задаче (6.1.1),

если 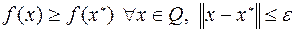при некотором .

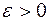Если 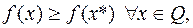то 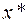– точка глобального минимума.

Множество 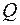называется выпуклым,

если при 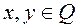точка 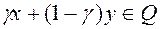для .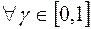

Теорема 1 (необходимое условие минимума 1 порядка). Пусть 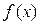дифференцируема в точке минимумаx 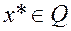, а 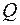–выпуклое множество. Тогда

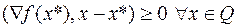. (6.1.2)

Доказательство производится от противного. Предполагается, что существует точка не удовлетворяющая (6.1.2). На основе этого предположения на луче 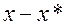находится точка с меньшим значением функции, что противоречит предположению, что 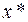– точка минимума.

Условие (6.1.2) означает, что множество 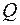и множество 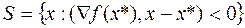, образованное направлениями локального убывания 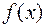не должны пересекаться.

Для выпуклой 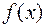удается сформулировать достаточное условие экстремума в терминах первой производной.

Теорема 2 (достаточное условие минимума 1 порядка). Пусть 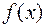дифференцируема в точке 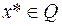, 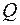–выпуклое множество и выполняется условие

,

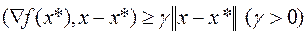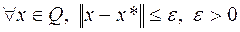. (6.1.3)

Тогда 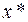–точка локального минимум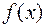а на .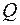

В условиях теоремы 2 минимум достигается на границе.

Теорема 3 (Необходимое и достаточное условие минимума 1 порядка). Пусть 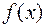выпуклая на 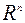и дифференцируемая в точке 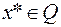функция. Тогда условие

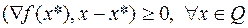, (6.1.4)

является необходимым и достаточным для того, чтобы 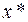был глобальным минимумом 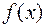на .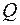

Существование и единственность минимума.

Теорема 4 (Вейерштрасса). Пусть 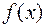–непрерывная на 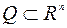, множество 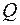замкнуто, а множество 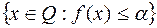ограничено и непусто для некоторого 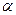. Тогда задача (6.1.1) имеет решение.

Если выполняется достаточное условие минимума (6.1.3), то минимум единственный.

Теорема 5 . В условиях теоремы 2 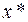–локально единственная точка минимума.

Как и в случае минимизации без ограничений, единственность решения гарантируется строгой выпуклостью функции .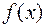

Дадим изложение основных методов решения задачи (6.1.1).

Метод проекции градиентаявляется обобщением градиентного метода, в котором выход за множество ограничений всякий раз компенсируется посредством перехода в точку проекции

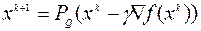, (6.1.5)

где операция проектирования определена выражением

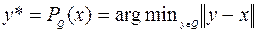. (6.1.6)

Теорема 6. Пусть 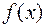– выпуклая дифференцируемая функция в 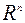, градиент которой удовлетворяет условию Липшица с константой 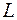. Пусть 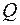выпуклое и замкнутое, 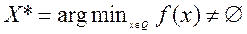и 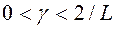. Тогда:

а) ;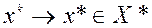

б) если 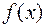сильно выпукла, то 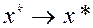со скоростью геометрической прогрессии;

в) если 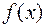дважды дифференцируема и 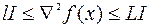, то знаменатель прогрессии равен ;

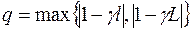Метод условного градиента. В его основе лежит идея линеаризации функции и использование линеаризации для вычисления направления спуска посредством минимизации методом проекции градиента полученной линейной функции на множестве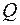

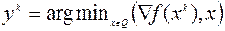, (6.1.7)

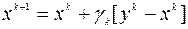. (6.1.8)

Предполагается что задача минимизации (6.1.7) имеет решение, что решение может быть найдено достаточно просто и указано правило выбора шагового множителя .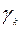

Теорема 7. Пусть f(x) – выпуклая дифференцируемая функция в 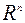, градиент которой удовлетворяет условию Липшица с константой 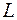. Пусть 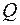выпуклое и замкнутое, 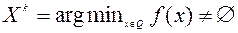и 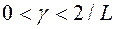. Тогда предельные точки 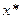последовательности 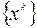– точки минимума 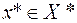и справедливы оценки:

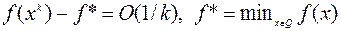(6.1.9)

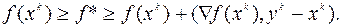(6.1.10)