Группоид. Квазигруппа. Латинский квадрат. Лупа. Полугруппа. Моноид. Группа. Абелева группа.

Группоид, обозначаемый символом (M, ·) — множество M, на котором задана некоторая бинарная операция, обозначаемая ·

Если множество M группоида конечно, то группоид конечный

Конечный группоид можно считать заданным, если выписана его таблица Кэли.

Квазигруппа(от латинского слова quasi ”почти” ) — группоид, бинарная операция которого (например, ·) такова, что каждое из уравнений a · x = b, y · a = b имеет единственное решение для любых элементов a, b этого множества.

Таблица Кэли квазигруппы – латинский квадрат таблица n×n, заполненная так, что в каждой строке и столбце встречались все n символов (каждый по одному разу)

Пример1: «*» на N – не квазигруппа, так как для a=2, b=3 уравнения a · x = b , y · a = b не разрешимы.

Пример2: «*» на Q - квазигруппа, так как для любых a, b уравнения a · x = b , y · a = b разрешимы и имеют единственное решение.

Пример3: Группоид A = ( M={a,b,c}, f1) задан таблицей Кэли не квазигруппа, так как уравнение a · x = b имеет два решения: а, с

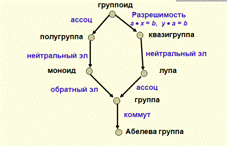
Типы группоидов

Лупа – квазигруппа с нейтральным элементов

Группа – лупа у которой бинарная операция ассциативна

Полугруппа – это группоид с ассоциативной операцией

Моноид - это полугруппа с нейтральным элементом е

Группа - это моноид в котором для каждого элемента существует обратный элемент

Абелева группа - это группа в которой операция коммутативна

Пример: (Z, «+») – квазигруппа, лупа, полугруппа, моноид,

группа, абелева группа

19.Подстановки. Композиция подстановок, нейтральная, обратная подстановка. Группа подстановок и ее таблица Кэли. Подгруппы группы подстановок.

Симметрическая полугруппа

Преобразования f конечного множества M называются подстановками множества M.

Если множество M содержит n элементов, то группа преобразований Sn множества M называется группой подстановок n-ой степени или симметрической группой n-ой степени.

Пример: Группа подстановок 3-ей степени. Дано M={a,b,c}. Число подстановок 6. Схема - в под каждым элементом указывается его образ.

Р1 – называется тождественной подстановкой

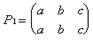
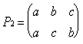
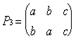
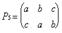
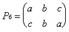
Композиция подстановок вначале выполняет правый сомножитель

потом левый

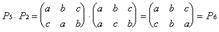
В Р2: а→а, далее символ а ищем среди прообразов подстановки Р5

(т.е. в верхней строке). Ему соответствует элемент (образ) с.

Итог Р5 ∙ Р2: a→с

Нейтральным элементом является тождественная подстановка Р1

Р1∙ f = f ∙ P1 = f

Обратную подстановку получаем перестановкой верхней и

нижней строки, например:

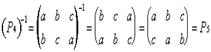
Таблица Кэли композиции подстановок

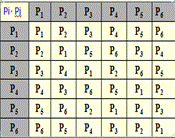
Чтобы по таблице найти обратную подстановку, надо в строчке, соответствующей рассматриваемой подстановки, найти нейтральный элемент P1; Столбец, в котором находится Р1 дает обратную подстановку. P4^-1 = P5

Группа – имеет нейтральный и обратный элемент, операция

ассоциативна Pi ∙ (Pj ∙ Pk) = (Pi ∙ Pj) ∙ Pk

Пример: Р2 ∙ (P3 ∙ P4) ? (P2 ∙ P3) ∙ P4

Р2 ∙ Р2 ? P5 ∙ P4

Р1 = Р1

Группа подстановок не абелева Pi ∙ Pj ≠ Pj ∙ Pi

Пример: P2 ∙ P3= Р5 ≠ P3 ∙ P2=Р4

Подгруппы группы подстановок

Теорема (критерий подгруппы). Непустое подмножество H группы G = <G; *> образует подгруппу, тогда и только тогда, когда:

для любых двух элементов a, b из H их композиция a * b принадлежит H;

для любого элемента a из H обратный ему элемент a^# также принадлежит H.

Группа подстановок имеет подгруппы

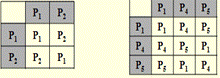
порядка 1: {P1}, порядка 2: {P1, P2}, {P1, P3}, {P1, P6}, порядка 3: {P1, P4, P5} и порядка 6: {P1, P2, P3, P4, P5, P6}.

Группа подстановок не абелева, но погруппы порядка 2,3 – абелевы (Pj ∙ Pj = Pj ∙ Pi). Пример: P4 ∙ P5= Р1 = P5 ∙ P4=Р1

Группа симметрий фигуры.