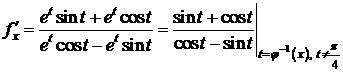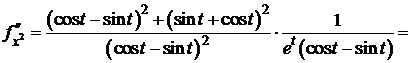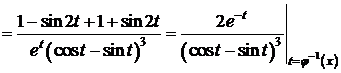Кривые и функции, заданные параметрически
Пусть точка движется по некоторой кривой АВ, то есть каждому моменту времени t соответствует определённая точка М(х;y) кривой АВ. Тогда
x=j(t) - закон движения точки по оси ОХ,
y=y(t) - закон движения точки по оси ОУ,
.
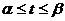(j и y должны быть дифференцируемы, т. к. существует скорость).
Уравнения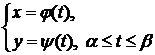 
(1)
полностью определяют кривую АВ. Переменная t (параметр), входящая в уравнения (1) может выражать не время, а другую физическую или геометрическую величину, то есть t – произвольный параметр.
Определение. Множество точек плоскости, координаты которых х и у удовлетворяют уравнениям (1), где j и y непрерывны на [α;β], называется кривой Жордана.
Уравнения (1) – параметрические уравнения кривой. Уравнения (1) задают не только совокупность точек, принадлежащих кривой, но и устанавливают порядок, в котором эти точки следуют друг за другом (при изменении t от α до β). При этом не исключено, что с одной и той же точкой (на рисунке точка К) движущаяся точка совместится дважды или более раз.
Точка M(x;y)=M(j(t);y(t)) кривой Жордана называется кратной, если она соответствует более, чем одному значению параметра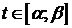 
. Если кривая не имеет кратных точек (то есть разным значениям t соответствуют разные точки кривой), то она называется простой кривой.
Если при t=β уравнения (1) определяют ту же точку кривой, что и при t=α, то есть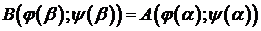 
, то кривая (1) называется замкнутой.
Если замкнутая кривая не имеет кратных точек, кроме А=В, то она называется простой замкнутой кривой.
Система (1) задаёт некоторую связь переменных х и у (какому-либо значению t соответствует определённое х и определённое у, значит, связь есть). Если из системы (1) удаётся исключить параметр t, то получаем уравнение кривой, связывающее координаты х и у.
Примеры.
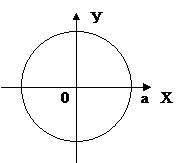
1) x=acost,
y=asint,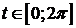 
,
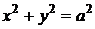- окружность с центром в точке (0;0) радиуса а.
2) x=acost,
y=bsint, ,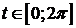
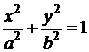- эллипс.
3) x=acost+x0,
y=asint+y0, ,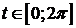
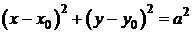- окружность с центром в точке 
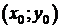, радиуса а.
4) x=a(t-sint),
y=a(1-cost).
Пусть по прямой Ох катится окружность радиуса а.
Циклоида - линия, которую при этом описывает каждая точка окружности.
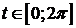- первая арка циклоиды
При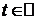 
получим всю циклоиду.
5) 
,
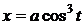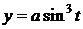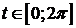, - астроида (гипоциклоида)
| t |  |  |  |  |  |  |  | |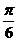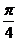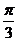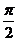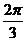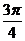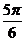
| х |  |  |  |  |  |  | ||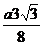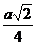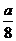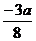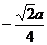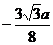
| y | |  | |  |  | |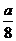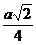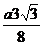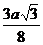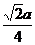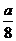
Построим по точкам.
| t |  |  |  |  |  |  |  |  |  |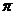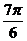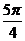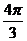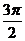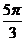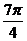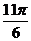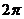
| х | -1 |  | |  | | |  | ||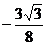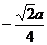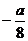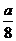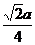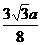
| y | 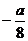| 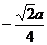| 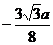| -1 | | | |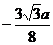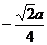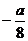
Из примеров видно, что кривая (1) не всегда является графиком некоторой функции, то есть уравнения (1) не всегда определяют функцию y=f(x) (хотя связывают х и у).
Пусть функция x=j(t) имеет обратную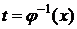 
, xÎX. Подставляя 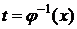в функцию y=y(t), получим 
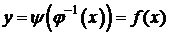, xÎX. Таким образом, если для функции x=j(t)существует обратная функция, то система (1) определяет функцию y=f(x).
Определение.Задание функции y=f(x) с помощью системы (1) называется параметрическим заданием функции.
Если в параметрически заданной функции уравнение x=j(t) разрешимо относительно t (t=t(x)), то параметрическое задание функции можно свести к явному: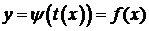 
(но это не всегда можно сделать).
Пример.x=acost,
y=asint,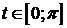 
,
x=j(t) монотонно убывает и непрерывна на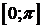 
, 
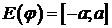. Следовательно, существует обратная функция 
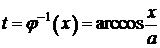, определённая на 
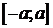. Значит, 
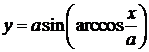- функция от х, определённая на 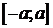.Так как 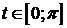, то y>0. Значит,
.
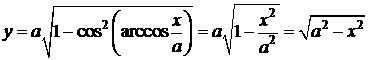Наоборот, всякую функцию y=f(x) можно многими способами представить параметрически в виде (1). Для этого достаточно задать совершенно произвольно функцию x=j(t) параметра t. Тогда для y=f(x) становится функцией того же параметра: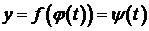 
.
Примеры.
1) 
, 
.
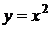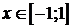Положим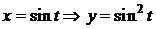 
. Получаем
x=sint,
, .
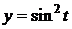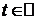2) y=f(x),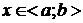 
.
x=t,
y=f(t),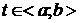 
.
Таким образом параметрический способ задания функции является более общим.
Теорема 1. Если в системе (1) функции j(t) и y(t) непрерывны на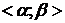 
и j(t) на этом промежутке строго монотонна, то система (1) определяет непрерывную функцию y=f(x), определённую на 
.
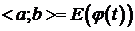Доказательство.
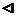Так как j(t) непрерывна на 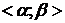, то по следствию из II теоремы Больцано-Коши. 
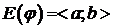. Так как x=j(t) непрерывна и строго монотонна на 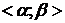, то она имеет обратную функцию 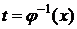, непрерывную и строго монотонную на 
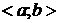. Тогда 
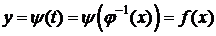- композиция двух непрерывных функций на 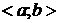, следовательно, она является непрерывной на 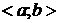функцией. 
Теорема 2. Пусть функция y=f(x) задана системой (1). Если функции j и y непрерывно дифференцируемы на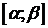 
, и на этом отрезке 
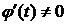, то функция f дифференцируема на некотором промежутке D и справедлива формула
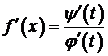
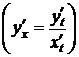. (2)
Доказательство.
Так как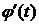 
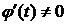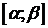непрерывна и на , то 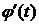одного знака на 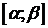(I теорема Больцано–Коши). Следовательно (это будет доказано позже), j(t) строго монотонна на 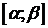. Значит, существует обратная функция 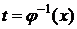, xÎD. Так как 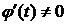, то обратная функция дифференцируема 
.
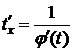Так как y=y(t), а 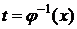, то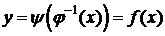 
- сложная функция. Она дифференцируема на D, так как j и y дифференцируемые функции, и её производная: 
.
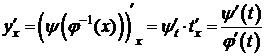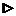
Пример. x=acost
y=asint, ,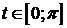 
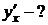
D j(t)=acost,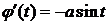 
непрерывна 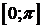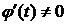на , на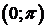 
,
y(t)=asint,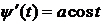 
, 
, 
, 
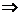
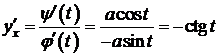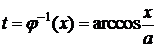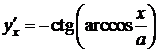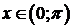. D
Замечание 1. Если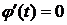 
, 
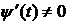, то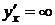 
.
Если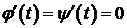 
, то в этой точке 
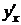не определена (хотя это не значит, что 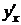не существует).
Например,рассмотрим функцию ,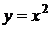 
, 
.
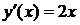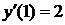Пусть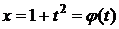 
, 
.
, 
.
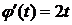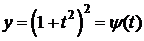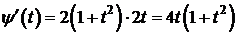Точке t=0 соответствует точка х=1.
, 
, 
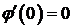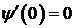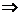
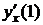не определена.
Если функции j(t),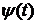 
дважды дифференцируемы и 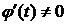, то существует 
:
.
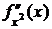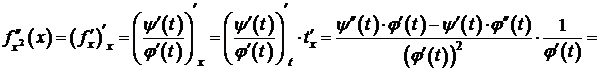
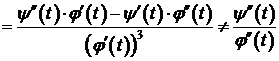Пример 1.
(*)
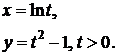x=j(t)=lnt - непрерывная, строго монотонная при t>0 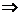существует обратная функция 
, 
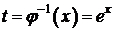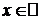. Тогда уравнения (*) задают на 
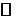функцию y=f(x). Найдём 
.
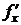I способ: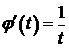 
, 
, ,
, 
,
, 
,
.
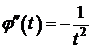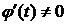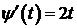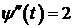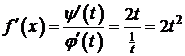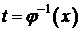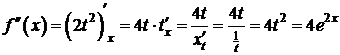II способ: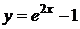 
, 
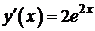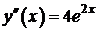(но не всегда 
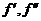выражаются через х).
Пример 2.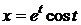 
, .
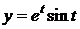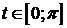На некотором промежутке эти формулы задают функцию y=f(x).
