Какими понятиями определяется интервальная оценка параметра? Какая существует между ними связь в виде формулы?

Для значимых параметров связи имеет смысл найти интервальные оценки.

При определении с надежностью γ доверительного интервала для значимого парного или частного коэффициентов корреляции ρ используют Z-преобразование Фишера и предварительно устанавливают интервальную оценку для Z

Z' - t 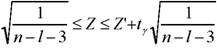(1.7)

где t_γ вычисляют по таблице интегральной функции Лапласа (табл. 1 приложения) из условия

Φ(t)=γ

Значение Z' определяют по таблице Z - преобразования (табл. 6 приложения) по найденному значению r. Функция нечетная, т. е.

Z'(-r) = -Z'(r).

Обратный переход от Z к ρ осуществляют также по таблице Z - преобразования, после использования которой получают интервальную оценку для ρ с надежностью γ :

r 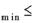ρ r.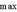

Таким образом, с вероятностью γ гарантируется, что генеральный коэффициент корреляции ρ будет находиться в интервале (rmin, rmax).

76. Построение интервальной оценки (доверительного интервала) (с надежностью 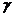) математического ожидания нормально распределенной случайной величины при известной дисперсии (вывод).

Х ~ N (a , δ), причем значение параметра a не известно, а значение дисперсии δ2 известно.

При Х ~ N (a , δ) эффективной оценкой параметра а является Х «с крышечкой», при этом Х «с крышечкой» ~ N (а, δ/√n). Статистика Z= Х «с крышечкой»-а|δ/√n имеет распределение N(0;1) независимо от значения параметра а и как функция параметра а непрерывна и строго монотонна. Следовательно, с учетом неравенства

ψа<ψ(Ө «с крышечкой», Ө) < ψа «с крышечкой»

и симметричности двусторонних критических границ распределния N (0;1)будем иметь:

Р(-uа < Z< ua )=1-a.

Решая неравенство -uа < Х «с крышечкой»-а|δ/√n < ua относительно а, получим, что с вероятностью 1-а выполняется неравенство:

Х «с крышечкой»-uа δ/√n <а<Х «с крышечкой»+ uа δ/√n

При этом

∆= uа δ/√n

что соответствует результату Р{|Z|≤ uа }=1-a, или Ф(uа) = (1-a)/2 число uа находят по таблице из условия Ф(uа) = (1-a)/2.

77. Построение интервальной оценки (доверительного интервала) (с надежностью 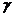) математического ожидания нормально распределенной случайной величины при неизвестной дисперсии (вывод).

Х ~ N (a , δ), причем числовые значения ни а ни δ² не известны. По случайной выборке найдем эффективную оценку параметра а: Х «с крышечкой» и оценку

_n

s²=1|n-1 *Σ(X_i-X «с крышечкой»)² параметра δ²

ⁱ⁼¹

Построение интервальной оценки для а основано на статистике

t(n-1)= X «с крышечкой»-а|s/√n, которая при случайной выборке из генеральной совокупности Х ~ N(a , δ) имеет распределение Стьюдента с (n-1) степенью свободы независимо от значения параметра а и как функция параметра а непрерывна и строго монотонна.

С учетом неравенства

Х «с крышечкой»-u_а δ/√n <а<Х «с крышечкой»+ u_а δ/√n и симметричности двусторонних критических границ распределения Стьюдента будем иметь:

Р(-t_a<t(n-1)< t_a)=1-a

Решая неравенство -t_a<X «с крышечкой»-а|s/√n< t_a относительно а, получим, что с вероятностью 1-а выполняется неравенство

Х «с крышечкой» -t_a s/√n< Х «с крышечкой»+t_a s/√n

и ошибка оценки Х «с крышечкой» при неизвестном значении параметра δ²

∆ t_a s/√n,

где число t_a находят по таблице при k=n-1 и p=a

Х «с крышечкой»- u_а s/√n<a< Х «с крышечкой»+ u_а s/√n где Ф(u_а)=(1-а)/2