Приведите известные вам формулы комбинаторики, которые используются при непосредственном исчислении вероятности по её классическому определению.

Приведите известные вам формулы комбинаторики, которые используются при непосредственном исчислении вероятности по её классическому определению.

A^m_n =n!/(n-m)!=n(n-1). . .(n-m+1) –размещения

P_n = n!=n(n-1)(n-2). . .1 – перестановки

C^m_n= A^m_n/P_m= n!/(m!(n-m)!) – сочетание

Приведите определение условной вероятности.

Условная вероятность – вероятность события В, вычисленную в предположении, что событие А уже наступило - P_A(B)

P_A(B) = P(AB)/P(A) (P(A)>0)

Зависимость и независимость двух событий (определение)

Два события называются независимыми, если вероятность одного из них не зависит от вероятности того, произошло или не произошло другое.

Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

12. Теорема умножения вероятностей для зависимых и независимых событий (формулировка)

Вероятность произведения двух независимых событий равно произведению вероятностей этих событий Р(АВ)=Р(А)Р(В).

Вероятность совместного появления двух событий равно произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило P(A)*P(C/A)=P(AC)

13. Сформулируйте условие, при котором для вычисления вероятности 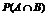следует применять теорему умножения для зависимых событий. Приведите формулировку этой теоремы.

При условии того, что из одного события «вытекает» другое.

Вероятность совместного появления двух событий равно произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило P(AC) = P(A)*P(C/A).

14. Сформулируйте условие, при выполнении которого можно утверждать, что событие 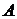не зависит от события ?

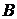если условная вероятность события В равно его безусловной вероятности: Ра(В)=Р(В)

15. Сформулируйте условие, при выполнении которого можно утверждать, что событие 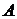зависит от события ?

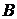два события называются зависимыми, если вероятность их совмещения не равна произведению вероятности этих событий!

Сформулируйте условие, при выполнении которого можно утверждать, что событие В зависит от события А.

Два события называются зависимыми, если вероятность их совмещения не равна произведению вероятности этих событий!

Докажите, что два несовместных события А и В (с положительными вероятностями наступления) всегда являются зависимыми.

P(Омега)= P(A+B)+P(A+B) (Последняя скобка сверху черта-«Не»)=1

P(Омега)= P(A)+P(B)+P(A+B) (Последняя скобка сверху черта-«Не»)=1

P(B)=1-P(A)- P(A+B) (Последняя скобка сверху черта-«Не»)

18. Сформулируйте условия, при выполнении которых можно утверждать, что гипотезы Н₁, Н₂, Н_n образуют полную группу событий.

Говорят, что события H1, H2, …, Hn образуют полную группу, если они попарно несовместны (H_i ∩H_j = ∅, i ≠ j), и их объединение эквивалентно достоверному событию (H₁ ∪H₂ ∪ ··· ∪H_n = Ω).

Сформулируйте условия, при выполнении которых можно для вычисления вероятности некоторого события А можно использовать формулу полной вероятности. Приведите формулировку и краткое доказательство формулы полной вероятности.

Если события H1, H2, …, Hn ∈ S образуют полную группу и имеют положительные вероятности, то для любого события A ∈ S

n

P(A)=P(A│H₁)P(H₁)+P(A│H₂)P(H₂)+…+P(A│H_n)P(H_n)= ∑P(A│H_i)P(H_i).

i=1

В соответствии с этой формулой вероятность наступления события A может быть представлена как сумма произведений условных вероятностей события A при условии наступления событий Hi на безусловные вероятности этих событий Hi. Поскольку среди событий H1, H2, …, Hn, образующих полную группу, в результате опыта должно наступить одно и только одно, эти события Hi называют гипотезами (i = 1, 2, …, n).

Доказательство. Очевидно, A = (A∩H1)∪(A∩H2)∪ · · · ∪(A∩Hn), причем события (A∩H1), (A∩H2), …, (A∩Hn) несовместны (поскольку несовместны события H1, H2, …, Hn). По аксиоме аддитивности вероятности P(A) = P(A∩H1) + P(A∩ | H2)P(H2) + ··· + P(A∩Hn). Каждую из вероятностей P(A∩Hi) раскроем по формуле умножения вероятностей: P(A∩Hi) = P(A | Hi)P(Hi) (i = 1, 2, …, n). Подставляя, получаем: P(A) = P(A | H1)P(H1) + P(A | H2)P(H2) + · · + P(A | Hn)P(Hn), что и требовалось доказать. 􀂉

Формула полной вероятности остается справедливой и в случае, если условие, состоящее в том, что события H1, H2, …, Hn образуют полную группу, заменить более слабым: гипотезы H1, H2, …, Hn попарно несовместны (Hi ∩Hj = ∅ при i ≠ j), а событие A влечет за собой объединение этих гипотез (A ⊆ H1∪H2∪ ··· ∪Hn).

Правило «Трех сигм»

Теоретически нормальная плотность вероятности отлична от 0 в любой, даже очень отдаленной от а точки х, однако практически почти вся вероятность сосредоточена на отрезке а 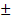3σ (отсюда и название.

В самом деле,

P{a-3σ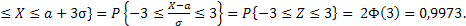

Таким образом, вероятность попадания вне этого отрезка равна всего 0,0027.

Что такое совместный ряд распределений дискретной двумерной случайной величины? Укажите его свойства. Как построить по этому ряду распределения ряды распределения компонент дискретной двумерной случайной величины?

Что такое совместная плотность распределения непрерывной двумерной случайной величины? Укажите ее свойства. Как построить по плотности совместного распределения плотности распределения и функции распределения компонент этой непрерывной двумерной случайной величины?

Плотностью совместного распределения вероятностей (двумер-ной плотностью вероятности) непрерывной двумерной случайной величины называ-ется смешанная частная производная 2-го порядка от функции распределения:

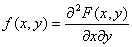. (8.2)

Замечание. Двумерная плотность вероятности представляет собой предел отношения вероятности попадания случайной точки в прямоугольник со сторонами Δх и Δу к площади этого прямоугольника при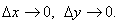

Свойства двумерной плотности вероятности.

1) f(x, y) ≥ 0 (см. предыдущее замечание: вероятность попадания точки в прямоуголь-ник неотрицательна, площадь этого прямоугольника положительна, следовательно, предел их отношения неотрицателен).

2) 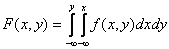(cледует из определения двумерной плотности вероятно-сти).

3) 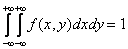(поскольку это вероятность того, что точка попадет на плос-кость Оху, то есть достоверного события).

Как построить бла-бла-бла к сожалению не нашла!

Сформулируйте определение и напишите формулу для вычисления корреляционного момента (коэффициента ковариации) двух случайных величин. Докажите, что для независимых случайных величин его значение равно нулю.

Корреляционным моментом СВ x и h называется мат. ожидание произведения отклонений этих СВ. m x h =М((x —М(x ))*(h —М(h )))

Для вычисления корреляционного момента может быть использована формула:m x h =М(x *h )—М(x )*М(h ) Доказательство: По определению m x h =М((x —М(x ))*(h —М(h ))) По свойству мат. ожидания

m x h =М(x h —М(h )—h М(x )+М(x )*М(h ))=М(x h )—М(h )*М(x )—М(x )*М(h )+М(x )*М(h )=М(x h )—М(x )*(h )

Предполагая, что x и h независимые СВ, тогда m x h =М(x h )—М(x )*М(h )=М(x )*М(h )—М(x )*М(h )=0; m x h =0. Можно доказать, что если корреляционный момент=0, то СВ могут быть как зависимыми, так и независимыми. Если m x h не равен 0, то СВ x и h зависимы. Если СВ x и h зависимы, то корреляционный момент может быть равным 0 и не равным 0. Можно показать, что корреляционный момент характеризует степень линейной зависимости между составляющими x и h . При этом корреляционный момент зависит от размерности самих СВ. Чтобы сделать характеристику линейной связи x и h независимой от размерностей СВ x и h , вводится коэффициент корреляции:

Кx h =m x h /s (x )*s (h ) Коэффициент корреляции не зависит от разностей СВ x и h и только показывает степень линейной зависимости между x и h , обусловленную только вероятностными свойствами x и h . Коэффициент корреляции определяет наклон прямой на графике в системе координат (x ,h ) Свойства коэффициента корреляции.

1. -1<=Кx h <=1

Если Кx h =± 1, то линейная зависимость между x и h и они не СВ.

1. Кx h >0, то с ростом одной составляющей, вторая также в среднем растет.

Кx h <0, то с убыванием одной составляющей, вторая в среднем убывает.

1. D(x ± h )=D(x )+D(h )± 2m x h

Доказательство.

D(x ± h )=M((x ± h )2)—M2(x ± h )=M(x 2± 2x h +h 2)—(M(x )± M(h ))2=M(x 2)± 2M(x h )+M(h 2)—+M2(x )+2M(x )*M(h )—M2(h )=D(x )+D(h )± 2(M(x h ))—M(x )*M(h )=D(x )+D(h )± 2m x h

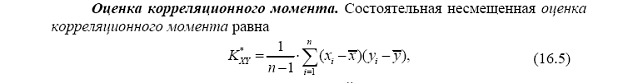
Сформулируйте определение коэффициента корреляции двух случайных величин. Докажите, что его значение не может превышать единицы по абсолютной величине. Докажите, что его значение равно единице по абсолютной величине, если случайные величины связаны линейной зависимостью.

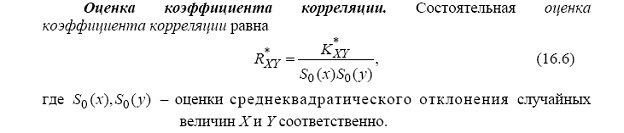
Доказать теорему Чебышева.

Если независимые случайные величины 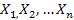имеют математические ожидания 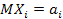и ограниченные в совокупности дисперсии 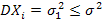, то разность средних арифметических случайных величин и средних их математических ожиданий сходится по вероятности к нулю: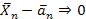

В самом деле, применим неравенство Чебышева к случайной величине 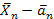. Поскольку

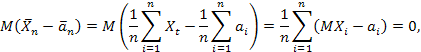
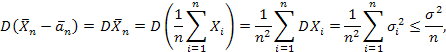
то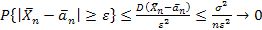

Следовательно,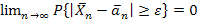

таким образом, действительно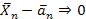

Что такое ошибка 1-го рода?

состоит в том, что будет отвергнута правильная нулевая гипотеза. Вероятность ошибки первого рода называют уровнем значимости и обозначают через a.

Что такое ошибка 2-го рода?

состоит в том, что будет принята неправильная нулевая гипотеза. Вероятность ошибки второго рода обозначают через b.

Приведите известные вам формулы комбинаторики, которые используются при непосредственном исчислении вероятности по её классическому определению.

A^m_n =n!/(n-m)!=n(n-1). . .(n-m+1) –размещения

P_n = n!=n(n-1)(n-2). . .1 – перестановки

C^m_n= A^m_n/P_m= n!/(m!(n-m)!) – сочетание