Эйлеровы и гамильтоновы пути и циклы

Эйлеров путь (цикл) в графе – это путь (цикл), проходящий все рёбра графа по одному разу. Гамильтонов путь (цикл) – это простой путь (цикл), обходящий все вершины графа.

Конечно, эйлеров (или гамильтонов) путь или цикл существует далеко не во всяком графе. Обязательное требование на граф для существования эйлерова (гамильтонова) пути/цикла – это связность графа. Но этого, вообще говоря, недостаточно. Необходимые и достаточные условия существования эйлерова пути/цикла даёт следующая теорема.

Теорема.Пусть – связный граф. Тогда:

1) эйлеров путь (незамкнутый) в существует в том и только том случае, если в точности две вершины имеют нечётные степени, а остальные – чётные;

2) эйлеров цикл в существует в том и только том случае, если все вершины имеют чётные степени.

Замечания.1.Данная теорема верна и для графов с кратными рёбрами. Наличие или отсутствие петель в графе не имеет значения.

2. Если в точности две вершины, скажем, 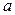и 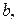имеют нечётные степени, то эйлеров путь, хотя и определяется неоднозначно, но обязательно должен иметь вершины 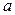и 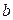своими концами.

Гамильтоновы пути/циклы имеют большое практическое значение. Например, если граф представляет собой сеть дорог, по которым может ходить курьер, то для обхода всех вершин графа курьеру следует идти по гамильтонову пути (если, конечно, такой путь существует). Ещё более сложной, чем нахождение какого-нибудь гамильтонова пути, является задача нахождения кратчайшего гамильтонова пути. С вычислительной точки зрения эти задачи (установить, существует ли гамильтонов путь, найти все гамильтоновы пути, найти кратчайший гамильтонов путь) являются сложными и требуют большого количества операций. В отличие от них, существует простой алгоритм нахождения эйлерова пути или цикла. Сформулируем его.

Алгоритм построения элерова пути/цикла. Пусть – связный граф и выполнены условия теоремы (т.е. либо все вершины чётной степени, либо ровно две имеют нечётную степень. Если все вершины чётные, то построение пути начинаем с любой вершины, а если две вершины нечётные, то начинаем именно с нечётной вершины. Пусть в качестве начала пути выбрана вершина 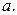Тогда мы идём из этой вершины в любую другую и убираем ребро, по которому только что прошли. Попав в следующую вершину, мы идём дальше и убираем только что пройденное ребро. И т.д. Надо только следить за тем, чтобы ребро, по которому мы хотим пройти, не было перешейком (перешейком называется ребро, удаление которого из графа нарушает связность – см. рис. 3.27). Можно доказать, что при реализации алгоритма, если все 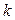рёбер, исходящих из текущей вершины, являются перешейками, то 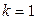(т.е. данная вершина – висячая). В этом случае мы идём по этому ребру и удаляем не только ребро, но и вершину, из которой только что шли по этому ребру. В конце концов мы придём во вторую нечётную вершину (если ровно две вершины графа были нечётные) или в начальную вершину пути (если все вершины были чётные).

Упражнение 3.22. Выяснить, имеет ли граф, изображённый на рисунке 3.28а, эйлеров путь или цикл, и если имеет, то построить его.

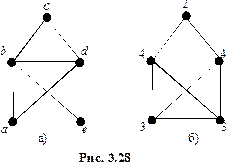Решение. Напишем на каждой вершине графа степень вершины (см. рис. 3.28б). Так как ровно две вершины имеют нечётные степени (это вершины 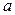и 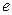), то существует эйлеров путь, и он идёт из вершины 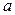в вершину 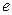или наоборот. Начнём путь с вершины 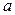и применим алгоритм. Тогда получим путь

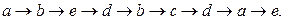
Отметим, что наличие у графа эйлерова пути или цикла означает возможность нарисовать граф, не отрывая карандаша от бумаги.

Упражнение 3.23. Выяснить, существует ли гамильтонов путь или цикл в графе, изображённом на рисунке 3.29.

Решение. Заметим, что если в графе есть вершина, после удаления которой граф распадается на 3 или более компонент связности, то у него не может быть гамильтонова пути или цикла. Действительно, пусть вершина с вышеуказанным свойством существует. Обозначим её через 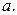Если бы в графе гамильтонов путь (или цикл) существовал, то по этому пути (или циклу) мы проходили бы через вершину 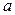более одного раза, что противоречит определениям. В графе на рисунке 3.29 такая точка 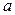есть. Значит, у него нет гамильтонова пути или цикла.

Планарные графы

Граф называется планарным, если он имеет плоскую укладку, т.е. такое изображение на плоскости, при котором рёбра графа не имеют общих внутренних точек. Например, граф 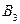планарен (см. рис. 3.30). Граф 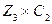также планарен (см. рис. 3.26).

Однако, существуют и непланарные графы. Условия планарности графа будут рассмотрены позже.

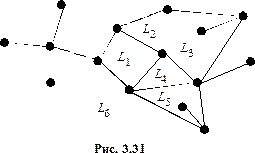Связный планарный граф, если его изобразить на плоскости без самопересечения рёбер, будет определять некоторую карту, которая состоит из областей, на которые разбивают плоскость рёбра графа (при этом вершины и рёбра, не входящие ни в один цикл, игнорируются). Эти области мы будем называть гранями (так как часто карта является развёрткой многогранника) или странами (см. рис. 3.31).

Одна из стран неограниченная – её называют океаном. На рисунке 31 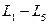– ограниченные страны, 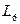– океан.

Пусть 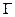– количество граней в данной плоской укладке планарного графа. Тогда справедлива формула Эйлера:

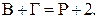(7)

Равенство (7) верно и для планарных графов с кратными рёбрами.

Для данной плоской укладки планарного графа обозначим через 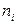количество 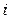-угольных граней ( 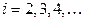). То есть 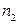– количество двуугольников (они могут присутствовать у графа с кратными рёбрами), 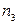– количество треугольников, 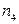– четырёхугольников и т.д. в плоской укладке. Тогда имеют место соотношения

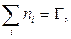
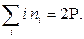(8)

С помощью этих соотношений можно доказывать непланарность графов.

Упражнение 3.24. Доказать, что граф 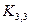не планарен.

Решение. Предположим, что граф 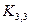планарен. Рассмотрим какую-либо его плоскую укладку. Пусть 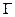– количество граней в плоской укладке. Ясно, что у графа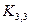 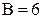и 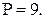По формуле (7) получаем: 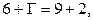откуда 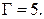Подставим эти цифры в соотношение (8_). Получим:

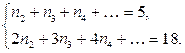
Заметим, что 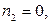так как у графа 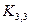нет кратных рёбер. Кроме того, 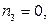так как граф 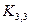не имеет циклов длины 3. Поэтому получаем:

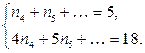
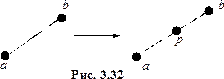Вычтем из второго уравнения первое, умноженное на 4, получим: 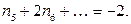Но это равенство невозможно, так как все 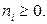Таким образом, граф 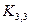не планарен.

Операцией разделения ребр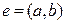а графа будем называть переход от графа к графу 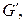который получается из графа добавлением вершины 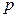и заменой ребра 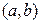двумя рёбрам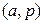и и (см. рис. 3.32).

Графы 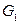и 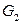называются гомеоморфными, если из графа 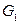применением несколько раз операции разделения ребра можно получить некоторый граф 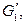а из графа 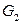– граф 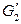такие, что 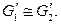Гомеоморфизм графов – более слабое условие, чем изоморфизм (любые два изоморфных графа гомеоморфны, но не наоборот). Например, графы 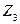и 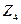гомеоморфны друг другу, но не изоморфны. Необходимое и достаточное условие планарности графа даёт следующая теорема.

Теорема Понтрягина – Куратовского.Граф планарен в том и только том случае, если у него нет подграфов, гомеоморфных графу 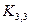или графу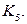

Упражнение 3.25. Показать с помощью теоремы Понтрягина – Куратовского, что граф 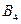не планарен.

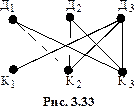Решение. Граф 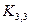образно называют “три дома – три колодца” (см. рис. 3.33).Это название возникло от старинной задачи: даны 3 дома и 3 колодца; можно ли от каждого дома к каждому колодцу провести дорожку так, чтобы эти дорожки не пересекались? Непланарность графа 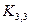доказывает несуществование дорожек, удовлетворяющих условиям задачи.

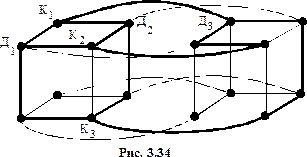Непланарность графа 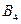(это 4-мерный куб, см. рис. 3.7) будет доказана, если мы найдём у него подграф, гомеоморфный графу 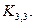Это делается несложно, решение можно увидеть на рисунке 3.34.

Раскрашивание графов

В теории графов рассматриваются раскрашивания вершин, рёбер, а для графов, имеющих укладку на какой-либо поверхности (например, для планарных графов), – также раскрашивание граней.

Пусть 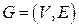– граф. Правильным раскрашиванием вершин называется отображение такое, что 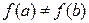для любых двух смежных вершин 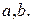Отображение 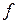интерпретируется как раскрашивание вершины 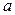в цвет с номером 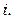Часто вместо натуральных чисел 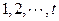используют символы 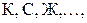обозначающие соответственно красный, синий, жёлтый и т.д. цвет.

Хроматическим числом 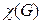графа называется наименьшее количество цветов, необходимых для правильного раскрашивания вершин графа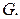

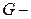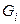Пусть граф, состоящий из компонент связности Так как компоненты раскрашиваются независимо друг от друга, то имеет место соотношение

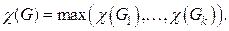(9)

Чтобы вычислить хроматическое число 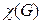конкретного графа надо не только найти правильную раскраску вершин, но также убедиться в том, что меньшим числом красок обойтись нельзя. Часто это требует значительных усилий.

Для полного графа 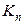мы имеем 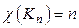– действительно, так как любые две вершины графа 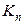смежны, то при правильной раскраске все вершины должны быть раскрашены в разные цвета.

Упражнение 3.26. Граф 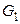получен из графа 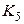удалением двух смежных, а граф 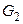– двух несмежных рёбер. Вычислить хроматические числа 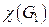и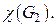

Решение. Графы 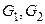изображены на рисунке 3.35.

Граф 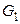содержит подграф, изоморфный 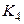(это подграф с вершинами 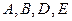), поэтому Иными словами, вершины 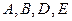должны быть раскрашены в разные цвета. Вершине 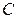можно присвоить такой же цвет, какой имеют 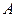или 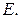Таким образом,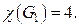

В графе 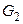вершины 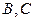и 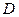должны быть раскрашены в разные цвета (т.к. они смежны друг с другом), поэтому 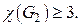Непосредственная проверка показывает, что трёх цветов достаточно (вершины 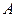и 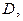а также вершины 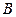и 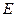могут быть закрашены в один цвет). Следовательно,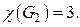

Правильная раскраска графов 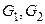изображена на рисунке 3.36.

Граф называется бихроматическим, если 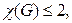т.е. если для раскраски вершин нужно не более двух красок.

Конечно, среди бихроматических наибольший интерес представляют графы, у которых 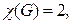так как 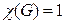лишь у графа, не имеющего ни одного ребра. Формула (9) показывает, что бихроматичность графа равносильна бихроматичности каждой его компоненты связности. Оказывается, что бихроматические графы имеют довольно простую характеризацию, которая задается простой теоремой.

Теорема. Следующие условия на граф эквивалентны:

(1) бихроматический;

(2) не имеет циклов нечетной длины;

(3) двудольный.

Проиллюстрируем эту теорему примером. А именно, докажем, что графы 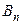при всех 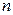являются бихроматическими. Это ясно для графов 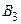и 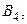правильная раскраска которых изображена на рисунке 3.37.

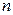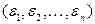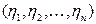Для произвольного проведём следующие рассуждения. Пусть и – вершины графа 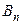(здесь 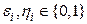). Так как смежные вершины отличаются лишь одной компонентой ( 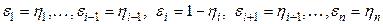), то у них 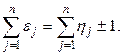Следовательно, для смежных вершин суммы 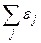и 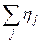разной чётности. 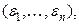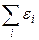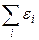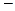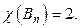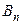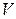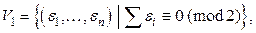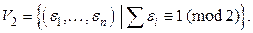Таким образом, если раскрасить вершины у которых сумма чётная, в один цвет, а те, у которых нечётная, в другой цвет, то смежные вершины будут раскрашены в разные цвета, а значит, Двудольность графа также ясна: если – множество вершин этого графа, то пусть а Тогда 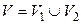– разбиение множества вершин, причём рёбра могут соединять лишь вершины из разных множеств

Рассмотрим теперь раскладку планарного графа 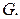Ввиду соотношения (9) мы можем считать, что – связный граф. Возьмём какую-либо его плоскую укладку. Добавление или удаление висячих вершин (вместе с инцидентными им рёбрами) не изменяет хроматического числа, поэтому будем считать, что висячих вершин нет. Разрешим графу иметь кратные рёбра, но запретим наличие петель. Тогда граф будет представлять собой карту на плоскости.

Сопряжённым графом 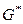назовем граф, полученный из графа следующим образом. Вершинами графа 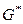являются грани графа (области в плоской укладке), и две вершины соединены ребром в том и только том случае, если соответствующие грани имеют границу (общее ребро). При этом две грани могут иметь более одного общего ребра 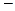тогда в графе 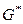будут кратные рёбра (это возможно даже в том случае, когда у графа нет кратных рёбер). Построение графа 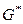изображено на рис. 3.38. Понятно, что граф 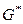тоже имеет плоскую укладку. На рис. 3.38а рёбра графа изображены сплошными линиями, а рёбра графа 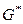пунктирными. На рис. 3.38б показан отдельно граф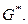

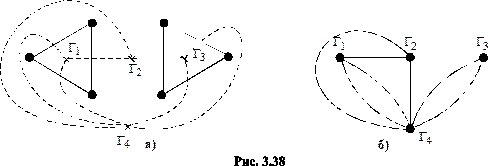
Обозначим количества вершин, рёбер и граней графа 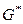соответственно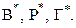

Из построения графа 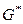видно, что каждой грани графа соответствует единственная вершина графа 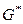и наоборот. Поэтому 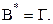Далее, каждое ребро графа пересекает единственное ребро графа 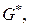что определяет взаимно однозначное соответствие между рёбрами графов и 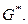Это означает, что 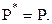Наконец, так как 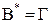и 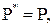то ввиду формулы Эйлера (7) мы получаем равенство 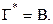Таким образом, мы имеем:

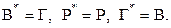(10)

Заметим, что на рисунок 38а можно смотреть и по-другому. Допустим, у нас есть граф 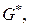но нет пока графа 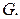Тогда из рисунка 38а видно, что если мы будем строить граф, сопряжённый с 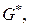то получим наш исходный граф 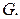Следовательно, свойство графов быть сопряжёнными друг к другу является взаимным, т.е. 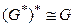(при подходящем выборе плоской укладки).

Раскрашивание граней планарного графа определяется аналогично раскрашиванию вершин. А именно, при правильном раскрашивании грани, имеющие общие граничные рёбра, должны быть окрашены в разные цвета (грани, имеющие лишь общую вершину, могут быть окрашены в один цвет).

Переход к сопряжённому графу позволяет раскраску вершин свести к раскраске граней и наоборот.

Л. Эйлер доказал, что для правильной раскраски граней любого планарного графа достаточно пяти красок. Эта теорема известна как теорема о пяти красках.

Теорема(Эйлер). Любая карта на плоскости (или сфере) имеет правильную раскраску не более, чем пятью красками.

Отсюда следует соответствующий результат для раскрашивания вершин.

Теорема. Для любого планарного графа

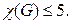
Ключевым моментом в теореме Эйлера является следующая лемма.

Лемма. Любой граф можно превратить в граф, у которого 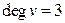для всех вершин 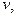следующим образом:

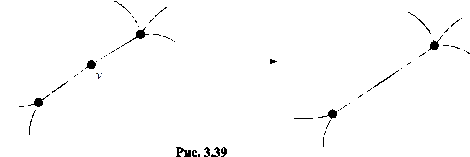
1) вершины степени 2 удаляются, а соответствующие рёбра “склеиваются” (см. рис. 3.39);

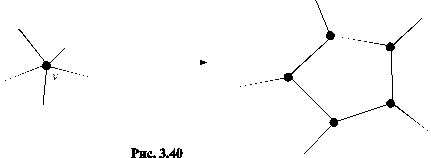
2) Вершина степени 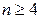заменяется п-угольником (см. рис. 3.40).

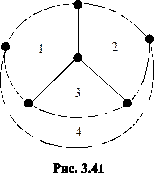Возникает вопрос: является ли число 5 точной границей хроматических чисел планарных графов? Другими словами, не хватит ли 3 или 4 красок? Граф, для раскраски граней которого не хватит 3 красок, приведён на рисунке 3.41.

Здесь грани 1,2,3,4 граничат каждая с каждой, поэтому должны быть закрашены в разные цвета (океану можно присвоить цвет, в который закрашена 3-я грань). Пример карты, для которой 4 цветов не хватит, а нужно все 5, никто не построил. Доказательство того, что для любой карты достаточно 4 цветов, было опубликовано Хейкеном и Аппелем в 1977 году, однако, с этим доказательством не все математики согласны, так как некоторые варианты было поручено перебрать компьютеру, результаты многочасовой работы которого проверить не представляется возможным.

Перейдём теперь к раскраске рёбер.

Правильной раскраской рёбер графа называется отображение 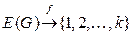такие, что 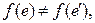если рёбра 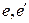имеют общую вершину. Числа 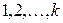– номера красок. Рёберным хроматическим числом 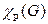графа называется наименьшее число красок, необходимых для правильной раскраски рёбер графа. Введём ещё одно число, характеризующее граф. А именно, пусть

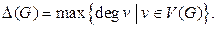(11)

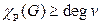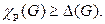Так как рёбра, выходящие из одной вершины, должны быть окрашены в разные цвета, то для любой вершины Отсюда следует, что Следующий замечательный результат показывает, что рёберное хроматическое число очень близко к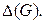

Теорема Визинга. Для любого графа имеет место неравенство

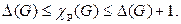(12)

Таким образом, если нам удастся найти раскраску ребер с количеством красок, равным 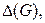то 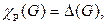а если мы докажем, что такой раскраски нет, то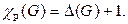

Упражнение 27. Вычислить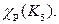

Решение. Пусть 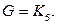Тогда 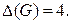Следовательно, 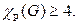Обозначим вершины графа буквами 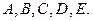Попробуем раскрасить рёбра в 4 цвета. Рёбра, выходящие из вершины 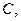должны быть окрашены в разные цвета 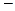допустим, это цвета 1,2,3,4. Напишем номера цветов на рисунке 3.42а.

На ребре 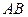написано 3,4 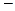это значит, что его можно окрасить в цвета 3,4, но нельзя в 1,2. Аналогичным образом понимаются записи на рёбрах 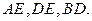Так как для ребра 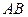цвета 3 и 4 со 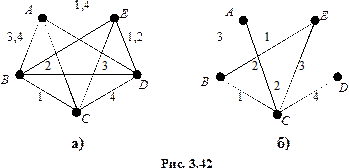вершенно равнозначны, то можно считать, что оно окрашено цветом 3. После этого однозначно окрашиваются рёбра: 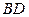– 2, 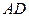– 1 (см. рис. 3.42б). Ребро 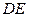не может быть окрашено ни одним из цветов 1,2,3,4. Следовательно, раскраска в 4 цвета невозможна. По теореме Визинга получаем, что 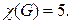Правильная раскраска рёбер в 5 цветов изображена на рис. 3.43.