Геометрическая вероятность – вероятность попадания точки в область (отрезок, часть плоскости и т.д.).

Геометрическая вероятность – вероятность попадания точки в область (отрезок, часть плоскости и т.д.).

Пусть отрезок CК лежит на отрезке АВ. На отрезок АВ наудачу поставлена точка. Это означает, что поставленная точка может оказаться в любой точке отрезка АВ, вероятность попадания точки на отрезок СК не зависит от его расположения относительно отрезка АВ и вычисляется по формуле

Р = длина СК / длина АВ.

А________С______К_______________В

Пусть плоская фигура М составляет часть плоской фигуры А.

На фигуру А наудачу брошена точка. Это означает, что брошенная точка может оказаться в любой точке фигуры А. Вероятность попадания брошенной точки на фигуру М не зависит ни от ее расположения относительно А, ни от формы фигуры М. Вероятность попадания точки в фигуру М определяется равенством

Р = Площадь М / Площадь А

Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества. При непосредственном вычислении вероятностей часто используют формулы комбинаторики. Приведем наиболее употребительные из них.

Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок

P_n = n!, где n! = 1 * 2 * 3 ... n.

Заметим, что удобно рассматривать 0!, полагая, по определению, 0! = 1.

Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений A^m_n = n (n - 1)(n - 2) ... (n - m + 1).

Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний С ^m_n = n! / (m! (n - m)!).

примеры перестановок, размещений, сочетаний

Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством A^m_n = P_mC ^m_n.

З а м е ч а н и е. Выше предполагалось, что все n элементов различны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам. Например, если среди n элементов есть n₁ элементов одного вида, n₂ элементов другого вида и т.д., то число перестановок с повторениями

P_n (n₁, n₂, ...) = n! / (n₁! n₂! ... ), где n₁ + n₂ + ... = n.

При решении задач комбинаторики используют следующие правила:

П р а в и л о с у м м ы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами.

П р а в и л о п р о и з в е д е н и я. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана mn способами.

Свойства дисперсии

Дисперсия постоянной величины с равна нулю.

Доказательство: по определению дисперсии

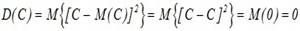
При прибавлении к случайной величине Х неслучайной величины с ее дисперсия не меняется.

D[X+c] = D[X].

Доказательство: по определению дисперсии

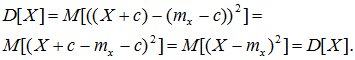(6.12)

3. При умножении случайной величины Х на неслучайную величину с ее дисперсия умножается на с².

Доказательство: по определению дисперсии

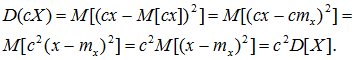. (6.13)

Для среднего квадратичного отклонения это свойство имеет вид:

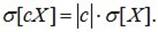(6.14)

Действительно, при ½С½>1 величина сХ имеет возможные значения (по абсолютной величине), большие, чем величина Х. Следовательно, эти значения рассеяны вокруг математического ожидания М[сХ] больше, чем возможные значения Х вокруг М[X], т.е. 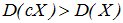. Если 0<½с½<1, то .

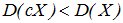Правило 3s. Для большинства значений случайной величины абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения, или, другими словами, практически все значения СВ находятся в интервале:

[ m - 3s; m + 3s; ].(6.15)

12. Распределения дискретных случайных величин. Биномиальное, Пуассона, геометрическое, гипергеометрическое распределения.

Исходной информацией для построения функции распределения дискретной случайной величины X является ряд распределения этой СВ.

xi	x1	x2	x3	...	xn	>xn
pi	p1	p2	p3	...	pn
F(xi)		p1	p1+p2	…	p1+..+pn-1

F(x_i)=P{X<x_i}=P{(X=x₁)È(X=x₂)È ... È(X=x_i-1)}= p₁+...+p_i-1.

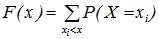, то есть суммирование распространяется на все значения 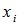, которые меньше х.

Функция распределения любой дискретной СВ есть разрывная ступенчатая функция, скачки которой происходят в точках, соответствующих возможным значениям случайной величины, и равны вероятности этих значений.

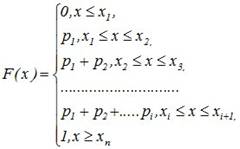
Биномиальное распределение.

Дискретная случайная величина X имеет биноминальное распределение, если ее закон распределения описывается формулой Бернулли:

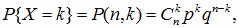
где p – параметр распределения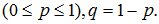

Распределение загасит от двух параметров п и р.

На практике биноминальное распределение возникает при следующих условиях. Пусть производится серия из п испытании, в каждом из которых некоторое событие появляется с вероятностью р. Случайная величина X, равная числу наступлений события в п опытах, имеет биноминальное распределение.

Числовые характеристики: М [Х] = n, D[X]= npq.

Название объясняется тем, что правую часть равенства можно рассматривать как общий член разложения Бинома Ньютона:

,

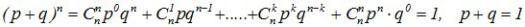т.е.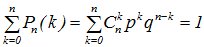

Распределение Пуассона.

Соотношениями, описывающими биноминальное распределение, удобно пользоваться в тех случаях, если величина и достаточно мала, а р велико.

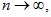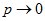Теорема: Если, а так, ч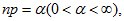то то

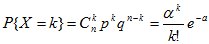
при любом k=0,1,….

Числовые характеристики: М[Х] = α, D[X] = α.

Закон Пуассона зависит от одного параметра α, смысл которого заключается в следующем: он является одновременно и математическим ожиданием и дисперсией случайной величины Х.

Нормальное распределение

Непрерывная случайная величина Х имеет нормальное распределение, если ее плотность вероятности имеет вид:

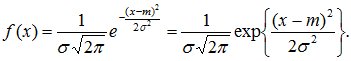(8.12)

Определим числовые характеристики нормально распределенной случайной величины Х. Математическое ожидание:

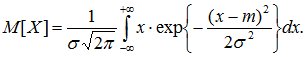
Применяя замену переменной

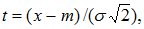(8.13)

получим

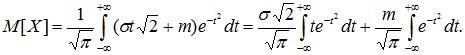
В полученном выражении первый интеграл равен нулю (интеграл в симметричных пределах от нечетной функции), а второй интеграл есть интеграл Эйлера-Пуассона:

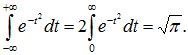(8.14)

Таким образом, математическое ожидание величины Х равно m:

M[X]=m.

Вычислим дисперсию СВ Х:

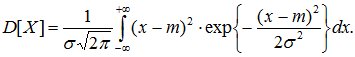
Применяя замену переменной (8.13) получим:

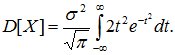
Интегрируя по частям, получим:

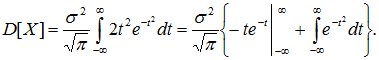
Первое слагаемое в фигурных скобках равно нулю (т.к. 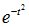при t→∞ убывает быстрее, чем возрастает любая степень t), второе слагаемое, согласно (8.14), равно 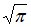, откуда

.

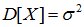Таким образом, нормальное распределение случайной величины полностью описывается двумя числовыми характеристиками: математическим ожиданием M[X] и средним квадратичным отклонением σ.

Рассмотрим влияние параметров m и σ на кривую распределения. При изменении параметра m кривая f(x), не изменяя формы, будет смещаться вдоль оси абсцисс. Изменение σ равносильно изменению масштаба кривой по обеим осям; например, при удвоении σ масштаб по оси абсцисс удвоится, а по оси ординат уменьшится в два раза (рис. 8.3).

Центральные моменты нечетной степени для нормально распределенной случайной величины определяются равны нуню; для вычисления центральных моментов четной степени используется рекуррентное соотношение следующего вида:

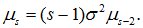(8.15)

Определим вероятность попадания нормально распределенной случайной величины в интервал от α до β:

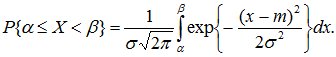
Сделав замену переменной t=(x-m)/σ, получим:

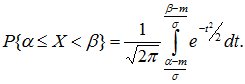
Так как первообразная для e^-x не выражается через элементарные функции, то для вычисления вероятностей событий, связанных с нормальными случайными величинами используют табулированную функцию Лапласа:

.

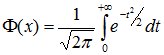С помощью этой функции вероятность попадания нормально распределенной случайной величины на интервал от α до β определится так:

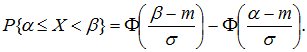(8.16)

Функция Лапласа обладает следующими свойствами:

1. Φ(0)=0;

2. Φ(-х)=-Φ(х);

3. Φ(-∞)=0,5.

Функция распределения нормально распределенной случайной величины через функцию Лапласа выражается так:

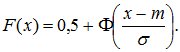(8.16)

Нормально распределенная случайная величина возникает в тех случаях, когда складывается много независимых (или слабо зависимых) случайных величин Х₁, Х₂, …, X_n. Тогда, каковы бы не были законы распределения отдельных случайных величин X_i, закон распределения их суммы будет близок к нормальному распределению. В частности, ошибки измерений распределяются по закону, близкому к нормальному.

показательное распределение — абсолютно непрерывное распределение, моделирующее время между двумя последовательными свершениями одного и того же события.

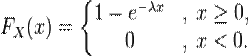
Случайная величина Х называется непрерывной, если ее функция распределения F(x) есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.

Так как для таких случайных величин функция F(x) нигде не имеет скачков, то вероятность любого отдельного значения непрерывной случайной величины равна нулю

P{X=α}=0 для любого α.

В качестве закона распределения, имеющего смысл только для непрерывных случайных величин существует понятие плотности распределения или плотности вероятности.

Вероятность попадания непрерывной случайной величины X на участок от x до x+Dx равна приращению функции распределения на этом участке:

P{x£ X <x+Dx}=F(x+Dx) - F(x).

Плотность вероятности на этом участке определяется отношением

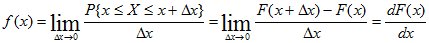(5.6)

Плотностью распределения (или плотностью вероятности) непрерывной случайной величины X в точке x называется производная ее функции распределения в этой точке и обозначается f(x). График плотности распределения называется кривой распределения.

Пусть имеется точка x и прилегающий к ней отрезок dx. Вероятность попадания случайной величины X на этот интервал равна f(x)dx. Эта величина называется элементом вероятности.

Вероятность попадания случайной величины X на произвольный участок [a, b[ равна сумме элементарных вероятностей на этом участке:

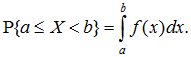(5.7)

В геометрической интерпретации P{α≤X<β} равна площади, ограниченной сверху кривой плотности распределения f(x) и опирающейся на участок (α,β) (рис. 5.4).

Это соотношение позволяет выразить функцию распределения F(x) случайной величины X через ее плотность:

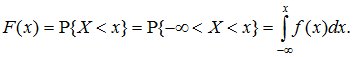(5.8)

В геометрической интерпретации F(x) равна площади, ограниченной сверху кривой плотности распределения f(x) и лежащей левее точки x (рис. 5.5).

Основные свойства плотности распределения:

1. Плотность распределения неотрицательна: f(x) ³ 0.

Это свойство следует из определения f(x) – производная неубывающей функции не может быть отрицательной.

2. Условие нормировки: 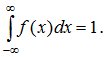Это свойство следует из формулы (5.8), если положить в ней x=∞.

Геометрически основные свойства плотности f(x) интерпретируются так:

1. вся кривая распределения лежит не ниже оси абсцисс;

2. полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.

Геометрическая вероятность – вероятность попадания точки в область (отрезок, часть плоскости и т.д.).

Пусть отрезок CК лежит на отрезке АВ. На отрезок АВ наудачу поставлена точка. Это означает, что поставленная точка может оказаться в любой точке отрезка АВ, вероятность попадания точки на отрезок СК не зависит от его расположения относительно отрезка АВ и вычисляется по формуле

Р = длина СК / длина АВ.

А________С______К_______________В

Пусть плоская фигура М составляет часть плоской фигуры А.

На фигуру А наудачу брошена точка. Это означает, что брошенная точка может оказаться в любой точке фигуры А. Вероятность попадания брошенной точки на фигуру М не зависит ни от ее расположения относительно А, ни от формы фигуры М. Вероятность попадания точки в фигуру М определяется равенством

Р = Площадь М / Площадь А

Комбинаторика изучает количества комбинаций, подчиненных определенным условиям, которые можно составить из элементов, безразлично какой природы, заданного конечного множества. При непосредственном вычислении вероятностей часто используют формулы комбинаторики. Приведем наиболее употребительные из них.

Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок

P_n = n!, где n! = 1 * 2 * 3 ... n.

Заметим, что удобно рассматривать 0!, полагая, по определению, 0! = 1.

Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений A^m_n = n (n - 1)(n - 2) ... (n - m + 1).

Сочетаниями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний С ^m_n = n! / (m! (n - m)!).

примеры перестановок, размещений, сочетаний

Подчеркнем, что числа размещений, перестановок и сочетаний связаны равенством A^m_n = P_mC ^m_n.

З а м е ч а н и е. Выше предполагалось, что все n элементов различны. Если же некоторые элементы повторяются, то в этом случае комбинации с повторениями вычисляют по другим формулам. Например, если среди n элементов есть n₁ элементов одного вида, n₂ элементов другого вида и т.д., то число перестановок с повторениями

P_n (n₁, n₂, ...) = n! / (n₁! n₂! ... ), где n₁ + n₂ + ... = n.

При решении задач комбинаторики используют следующие правила:

П р а в и л о с у м м ы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами.

П р а в и л о п р о и з в е д е н и я. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана mn способами.