Проверка гипотезы о виде плотности распределения

2.5.5.1. Критерий “хи-квадрат”

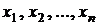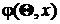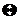Из генеральной совокупности X,образованной случайной величиной x, извлечена выборка . Выдвигается предположение о том, что плотность распределения случайной величины есть , где – вектор параметров. Для проверки этого предположения по выборочным данным вычисляются оценки параметров 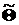и проверяется сложная гипотеза:

: плотность распределения случайной величины x есть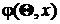

против альтернативы

: плотность распределения случайной величины xне .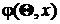

Поскольку эта гипотеза сложная, задается только вероятность ошибки первого рода a, которая в подобных случаях именуется уровнем значимости.

Степень различия между гистограммой и предполагаемой плотностью распределения выражается суммой квадратов разностей

,

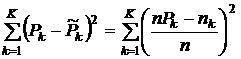где

,

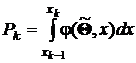то есть вероятность попадания значения случайной величины в интервал 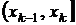при условии справедливости нулевой гипотезы, 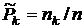- оценки этих вероятностей, где 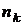– количество выборочных значений, попавших в интервал 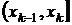, n – объем выборки, К– общее количество интервалов, на которых построена гистограмма.

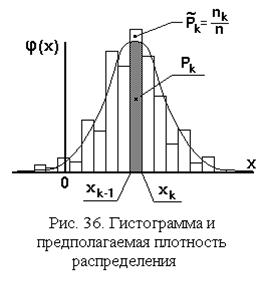Каждое слагаемое этой суммы является случайной величиной, поскольку случайным является число 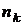. Если выборочные значения независимы, 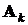– событие, которое заключается в том, что выборочное значение попадает в интервал 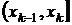, 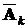– противоположное событие. Поэтому в соответствии со схемой Бернулли вероятность того, что при n экспериментах событие 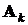произойдет ровно 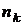раз, равна (см. разд. 1.3.2) .

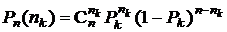Из результатов, полученных в примере разд. 1.3.5, следует, что

, .

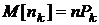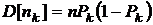Пользуясь формулами для моментов линейных функций от случайных величин, приведенными в разд. 1.3.4, можем записать, что

, .

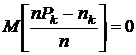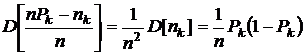Преобразуем исходную сумму путем деления каждого из слагаемых на его дисперсию. Получим сумму

.

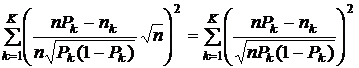Видно, что после этого деления

, .

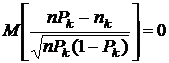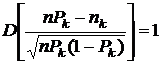Строго говоря, случайная величина

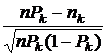
является дискретной из-за того, что порождена дискретной случайной величиной 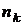, распределенной по биномиальному закону. При дискретности значений величины 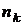, равной 1, дискретность значений вновь сформированной случайной величины равна 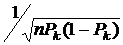, и с ростом n убывает до нуля. Поэтому можно говорить, что эта случайная величина в ассимптотике при n ® ¥ становится непрерывной.

С другой стороны, по теореме Муавра-Лапласа (см. разд. 1.3.7), распределение вероятностей случайной величины 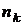при n ® ¥аппроксимируется значениями

.

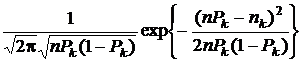После выполненных преобразований и с учетом того, что при n ® ¥дискретность значений случайной величины

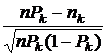
уменьшается до нуля, мы имеем право говорить, что эта случайная величина распределена асимптотически нормально с параметрами (0, 1), то есть

.

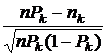
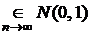Как известно из разд. 2.3.4.2, в), плотность распределения суммы квадратов таких случайных величин есть плотность распределения хи-квадрат. Таким образом, окончательно можем записать формулу для вычисления статистики критерия “хи-квадрат”, плотность распределения которой при условии справедливости нулевой гипотезы есть плотность распределения хи-квадрат с числом степеней свободы K - r, где K – количество слагаемых в сумме (то есть число интервалов, на которых построена гистограмма), r – число параметров предполагаемой плотности распределения, которые были определены по выборочным данным (то есть число связей, наложенных на выборочные данные):

.

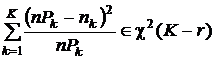Поскольку, как правило, 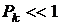сомножитель(1- 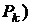в знаменателях слагаемых опущен.

Подобный функционал был использован нами ранее в разд. 2.3.6 для нахождения оценок параметров плотности распределения методом минимума .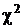

При заданной вероятности ошибки первого рода , здесь – уровня значимости, критическое значение 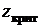(нижняя граница критической области ) назначается из следующих соображений.

При справедливости нулевой гипотезы маловероятно, чтобы статистика критерия оказалась слишком большой. Ограничимся таким критическим значением, вероятность превышения которого будет не более заданного значения a. Поскольку нам известно, что при условии справедливости нулевой гипотезы статистика критерия распределена приблизительно по закону 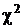, мы можем принять в качестве критического значения 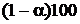– процентную квантиль .

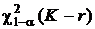Таким образом, сформирован критерий “хи-квадрат” проверки гипотезы о виде плотности распределения (или закона распределения) генеральной совокупности по экспериментальным данным.

П р о ц е д у р а п р о в е р к и г и п о т е з ы о виде плотности распределения по критерию “хи-квадрат”.

1. Задают уровень значимости a

2. По выборочным данным строят гистограмму в соответствии с указаниями разд. 2.2.

3. Вычисляются точечные оценки моментов.

4. Из теоретических соображений, по виду гистограммы, по соотношениям между моментами, по значениям асимметрии и эксцесса выдвигается гипотеза о виде плотности распределения .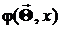

5. Вычисляются оценки rпараметров 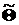предполагаемой плотности распределения, в результате будет получена плотность распределения .

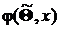6. С использованием 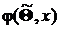вычисляются вероятности

.

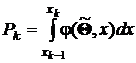7. Вычисляется статистика критерия

.

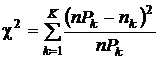8. Полученное значение сравнивается с критическим значением

,

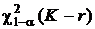где r – количество оцениваемых параметров предполагаемой плотности распределения .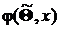

9. Если 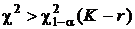делается вывод о том, что экспериментальные данные не подтверждают справедливость выдвинутой гипотезы или о том, что отсутствуют достаточные основания для того, чтобы считать нулевую гипотезу справедливой. Гипотеза пересматривается, выдвигается новая нулевая гипотеза, переход на п. 4 настоящей процедуры.

10. Если 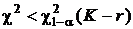делается вывод о том, что экспериментальные данные подтверждают справедливость выдвинутой гипотезы или о том, что имеются достаточные основания для того, чтобы считать нулевую гипотезу справедливой.

Сделаем замечание о том, что с уменьшением вероятности a возрастает критическое значение 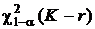, а это значит, что объективно растет вероятность ошибочного подтверждения нулевой гипотезы, когда она неверна. Крайний случай иллюстрирует это положение: если задать a = 0,то критическое значение 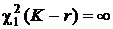, а это означает, что нулевая гипотеза, какой бы она ни была, не будет подвергаться сомнению ни при каком значении статистики критерия.

2.5.5.2. Критерий Колмогорова – Смирнова

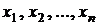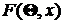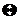Из генеральной совокупности X ,образованной случайной величиной x, извлечена выборка . По этим данным строится выборочная функция распределения, как это описано в разд. 2.2. По виду выборочной функции распределения выдвигается предположение о том, что функция распределения есть , где – вектор параметров. По выборочным данным вычисляются оценки параметров 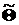, по соотношениям между ними уточняется вид функции распределения, и, если это нужно, ранее выдвинутое предположение уточняется. Проверяется сложная гипотеза

: функция распределения случайной величины x есть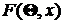

против альтернативы

: функция распределения случайной величины xне .

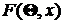Поскольку эта гипотеза сложная, задается только вероятность ошибки первого рода a, которая в подобных случаях именуется уровнем значимости.

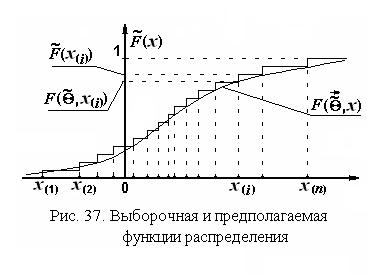
В соответствии с формулировкой гипотезы сравниваются две функции распределения: выборочная (см. разд. 2.2) и предполагаемая, представленные на рис. 37. Различие между ними определено, как

,

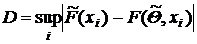где 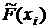– значения выборочной функции распределения при .

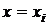Статистикой критерия является величина D. Критические значения табулированы. Таблицы критических значений 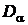как функций от вероятности a, приводятся практически во всех учебниках и справочниках по математической статистике. В таблице 6 приводятся некоторые часто употребляемые критические значения.

Таблица 6