Производящая функция моментов

Производящей функцией моментов случайной величины x называется математическое ожидание функции y(n)=exp(nx), где n – аргумент производящей функции моментов:

.

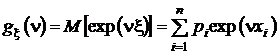Производящая функция моментов обладает рядом полезных свойств.

1) ;

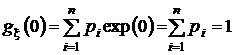2) Первая производная от 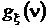по аргументу n:

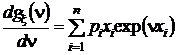,при n = 0 получим ;

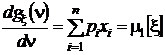3) Вторая производная от 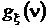по аргументу n:

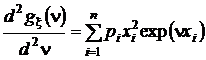,при n = 0 получим

;

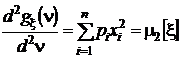4)k-я производная от 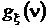по аргументу n:

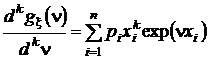,при n = 0 получим

.

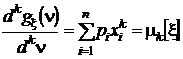Таким образом, чтобы получить значение k-го начального момента, достаточно продифференцировать производящую функцию моментов k раз по n и подставить в полученную производную n = 0.

П р и м е р. Написать производящую функцию моментов для биномиального распределения и вычислить математическое ожидание и дисперсию случайной величины, распределенной по биномиальному закону.

.

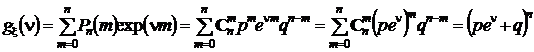Первая производная от 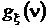по n

.

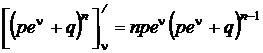Вторая производная от 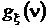по n

.

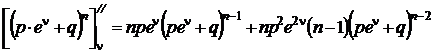Вычислим эти производные при n = 0:

, .

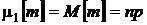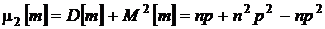Окончательно получим: M[m] = np, D[m] = np(1 – p) = npq.

Сопоставляя полученное выражение для математического ожидания числа появления события A в испытаниях по схеме Бернулли с наиболее вероятным значением этого числа, видим, что они совпадают.

З а м е ч а н и е о сходимости распределений вероятности и производящих функций моментов.

Пусть имеется последовательность распределений вероятностей дискретной случайной величины .

Пусть – производящие функции соответствующих распределений 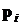из этой последовательности, которые также образуют последовательность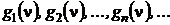

Если последовательность 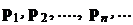сходится, имеет предел и пределом этой последовательности является распределение , то последовательность 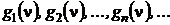также сходится, имеет предел, и ее пределом является производящая функция моментов предельного распределения. Справедливо и обратное утверждение.

Обратим внимание на то, что конструкция производящей функции моментов близка конструкции обратного дискретного преобразования Фурье, отсюда вытекают полезные свойства производящих функций моментов и близость их свойств свойствам дискретного преобразования Фурье.

Теорема Пуассона

Проанализируем асимптотическое поведение вероятности появления m событий в схеме Бернулли при n ® ¥, np=const= a. Цель – упрощение вычислений, трудоемкость которых сильно возрастает с ростом n.

Задача состоит в нахождении предела последовательности:

.

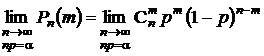Из равенства np =a следует, что p = 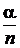. Кроме того,

.

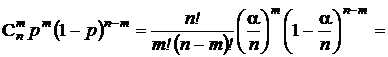
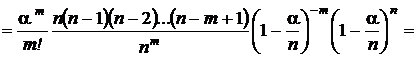
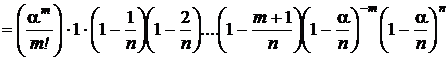В полученном выражении первый сомножитель не содержит n.Предел последнего сомножителя при n ® ¥равен 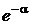. Пределы остальных сомножителей при n ® ¥равны 1. В результате получаем асимтотическое представление вероятностей из схемы Бернулли, или, что то же самое, биномиального распределения, в виде

.

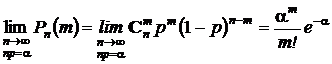Этот результат получен Пуассоном и успешно применяется для расчета вероятностей редких событий (при n ® ¥вероятность p стремится к 0) при массовых явлениях (испытаниях, опытах).

Полученные предельные значения вероятностей образуют в совокупности распределение вероятностей случайной величины. В самом деле,

.

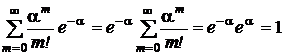Это распределение называется распределением Пуассона. Математическое ожидание и дисперсия этой случайной величины равны

M[m] = D[m] = a = np.

Производящая функция распределения Пуассона:

.

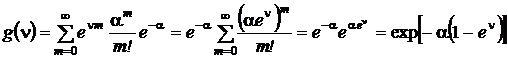1.3.7. Локальная теорема Муавра-Лапласа

В отличие от теоремы Пуассона теорема Муавра-Лапласа посвящена установлению асимптотики для вероятностей событий по схеме Бернулли при n ® ¥ и при p = const.

Здесь без вывода и доказательства приводится результат, полученный Муавром и Лапласом.

Напомним, что в разд. 1.3.5 были получены следующие выражения для математического ожидания и дисперсии случайной величины: числа появления события A при n испытаниях по схеме Бернулли

M[m] = np, D[m] = npq = np(1-p),

где p – вероятность появления события A при одном испытании.

В соответствии с локальной теоремой Муавра-Лапласа значения вероятностей 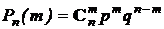при n ® ¥и p = constаппроксимируются функцией

.

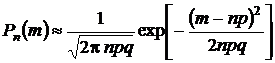Эта функция симметрична и имеет максимум при m = np.