П. 3. Формула полной вероятности

(следствие обеих основных теорем сложения и умножения)

Пусть событие А еще не произошло, но вскоре должно произойти. А может протекать в различных условиях, относительно характера которых сделано n гипотез Н₁, Н₂, …, Н_n, образующих полную группу несовместных событий. Вероятности гипотез известны. Тогда вероятность события А равна сумме произведений вероятности каждой гипотезы на вероятность события при этой гипотезе:

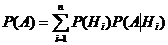– формула полной вероятности.

Доказательство.

По условию теоремы гипотезы Н₁, Н₂, …, Н_n образуют полную группу несовместных событий, следовательно, событие А может произойти с одной и только с одной гипотезой:

.

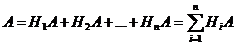Т.к. гипотезы несовместны, то и комбинации Н₁А, Н₂А, …, Н_nА – несовместны. Применим теорему 1:

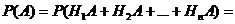
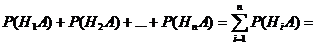(события А и Н_i – зависимы, т.е. надо применить теорему 3) = 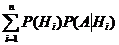. (что и треб. доказать)

Пример.

Имеется пять урн:

2 урны состава Н₁ – по 2 белых шара и 1 черному,

1 урна состава Н₂ – 10 черных шаров,

2 урны состава Н₃ – по 3 белых и 1 черному шару.

Наудачу выбирается урна и из нее наудачу выбирается шар. Чему равна вероятность события А = {будет вынут белый шар}?

Решение.

Событие А еще не произошло. Шар может быть вынут из урн разных составов, следовательно, в алгебре событий событие А запишется в виде: 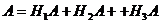. Тогда по формуле полной вероятности:

(*).

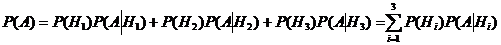Найдем отдельно вероятности событий:

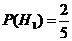(две урны состава Н₁ из пяти), , ,

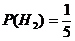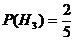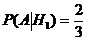(в каждой урне состава Н₁ 2 белых шара из трех),

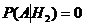( в урне состава Н₂ белых шаров нет),

.

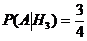Подставим найденные вероятности в формулу (*): .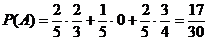

П. 4. Формула Байеса (Бейеса)

(следствие теоремы умножения и формулы полной вероятности)

Пусть событие А произошло,причем А могло протекать в различных условиях, относительно характера которых было сделано n гипотез Н₁, Н₂, …, Н_n, образующих полную группу несовместных событий. Вероятности гипотез известны. Требуется узнать, как изменяться вероятности гипотез в связи с появлением события А. Т.е. надо найти условную вероятность .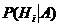

Решение.

По условию теоремы гипотезы Н₁, Н₂, …, Н_n образуют полную группу несовместных событий, следовательно событие .А произошло с одной и только с одной гипотезой:

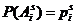, причем события А и Н_i – зависимы. Найдем вероятность произведения Н_iА, воспользовавшись теоремой 3:

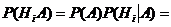(или, что то же самое) = 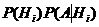, i = 1,2,…,n, отсюда

.

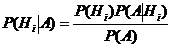Выразим Р(А) с помощью формулы полной вероятности:

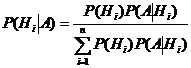– формула Байеса.

Пример.

Имеется пять урн:

2 урны состава Н₁ – по 2 белых шара и 3 черных шара,

2 урны состава Н₂ – по 1 белому и 4 черных шара,

1 урна состава Н₃ – 4 белых и 1 черный шар.

Из одной наудачу выбранной урны взят шар. Он оказался белым (событие А). Чему равна после опыта вероятность события, что шар вынут из урны третьего состава.

Решение.

Событие А произошло. Шар мог быть вынут из урн разных составов, следовательно, в алгебре событий событие А запишется в виде: .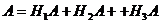

Найдем вероятности событий:

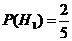(две урны состава Н₁ из пяти), , ,

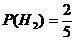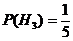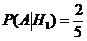(в каждой урне состава Н₁ 2 белых шара из пяти),

, .

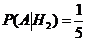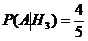По формуле Байеса найдем условную вероятность :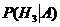

.
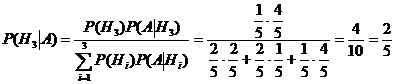