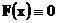Теорема единственности для характеристических функций и характеристические функции важных распределений

Соответствие между функциями распределения и характеристическими функциями является взаимнооднозначным. Каждой функции распределения соответствует одна и только одна характеристическая функция. Это свойство позволяет использовать характеристические функции для различения и определения распределений случайных величин. Прежде чем доказывать теорему единственности, подсчитаем характеристические функции наиболее важных распределений.

Название распределения	Характеристическая функция
Вырожденное в точке a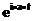
Биномиальное (n,p)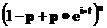
Геометрическое p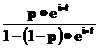
Пуассоновское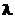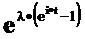
Нормальное стандартное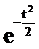
Нормальное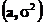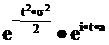
Равномерное на отрезке (0,1)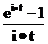
Равномерное на отрезке (a,b)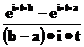
Бета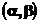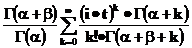
Экспоненциальное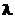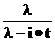
Гамма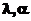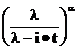

Заметим, что плотность и характеристическая функция стандартной нормальной случайной величины отличаются лишь множителем. Это позволяет нам доказать следующее важное равенство.

Равенство Парсеваля.

Пусть 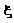- случайная величина с функцией распределения 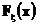и характеристической функцией ,

.

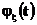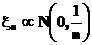Тогда плотность случайной величины 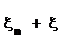можно представить в виде

.

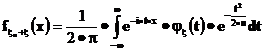Доказательство.

Пусть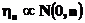

Рассмотрим очевидное равенство

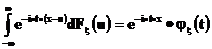
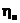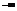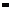умножим его на плотность случайной величины и проинтегрируем по tот до .Учитывая, что

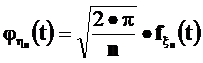
получим требуемое утверждение

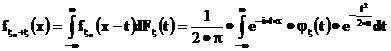
Доказательство завершено.

Меняя в доказательстве местами случайные величины 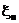и 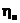получаем следующий вариант равенства Парсеваля

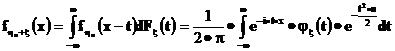
Очевидно, приведенные формулы справедливы и для несобственных функций распределения.

Теорема единственности для характеристических функций.

Соответствие между функциями распределения и характеристическими функциями является взаимнооднозначным.

Доказательство.

Интегрируя равенство

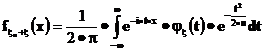
по отрезку [A,B], получаем

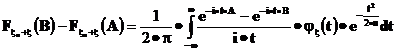
Левая часть этого равенства стремится к

,

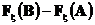а правая полностью зависит от 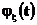. Таким образом функция распределения 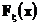определяется по 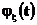однозначно.

Теорема доказана.

Формула

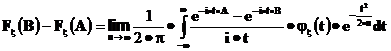
называется формулой обращения для характеристических функций.

Теорема непрерывности для характеристических функций

Важность характеристических функций для теории вероятностей определяется тем , что сходимость последовательности характеристических функций влечет за собой слабую сходимость последовательности соответствующих функций распределения.

Для того, чтобы это доказать, необходимо использовать следующую лемму и теорему.

Лемма о выборе.

Пусть 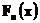- произвольная последовательность ограниченных в совокупности функций, заданных на прямой и 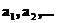- последовательность действительных чисел. Тогда существует подпоследовательность функций 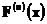которая сходится во всех точках 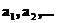к некоторой предельной функции .

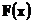Доказательство.

Для доказательства теорем применим диагональный метод Кантора.

Из курса математического анализа известно, что любая ограниченная числовая последовательность имеет сходящуюся подпоследовательность. Последовательность 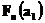следовательно, как ограниченная последовательность, имеет сходящуюся подпоследовательность 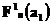. Из этой подпоследовательности выберем другую, сходящуюся в точке 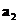- 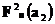и т.д. Тогда диагональная последовательность 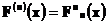сходится во всех точках

Доказательство закончено.

Выбрав в качестве множества точек множество рациональных чисел и учитывая что, функцию распределения достаточно задать лишь на всюду плотном множестве получаем следующую теорему.

Теорема о выборе.

Пусть 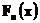- произвольная последовательность функций распределения. Тогда существует подпоследовательность последовательности 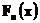, которая сходится во всех точках непрерывности к некоторой предельной неубывающей непрерывной слева функции .

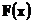Заметим, что функция 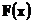не обязательно является функцией распределения, но (очевидно) обязательно является неубывающей функцией, такой что

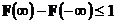
(несобственной функцией распределения).

Например, последовательность функций распределения 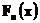случайных величин 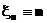сходится при 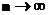к функции