Взаимосвязь различных видов сходимости

Взаимосвязь различных видов сходимости представлена на следующей диаграмме.

Заметим, что ни одну из стрелок на данной диаграмме нельзя, вообще говоря, повернуть назад, т.е. любые два вида сходимости неэквивалентны. Практическое значение имеют, в основном, слабая сходимость и сходимость в среднеквадратическом потому что они позволяют производить приближенные вычисления вероятностей и математических ожиданий и заменять одни математические модели другими. Остальные виды сходимости используются в основном при доказательстве слабой сходимости или исследовании качественных свойств модели. Поэтому более подробно исследуем взаимосвязи этих двух видов сходимости в остальными.

Покажем, вначале, что из сходимости по вероятности следует слабая сходимость.

Теорема (P->W).

Пусть

.

Тогда

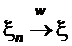
Доказательство.

Пусть x – точка непрерывности функции

.

Тогда

и

Таким образом

При малых и больших n левая и правая часть неравенства отличаются сколь угодно мало от , что доказывает теорему.

Доказательство завершено.

Обратная теорема верна при дополнительном условии.

Теорема (W->P).

Пусть

Тогда

Доказательство.

Доказательство завершено.

Покажем, что из сходимости в среднеквадратическом следует сходимость по вероятности.

Теорема (L²->P).

Пусть

Тогда

Доказательство.

Используем неравенство Маркова

.

Доказательство завершено.

Следующая теорема дает пример применения предыдущей теоремы для доказательства сходимости относительной частоты события к его вероятности в схеме Бернулли.

Закон больших чисел в форме Бернулли

Пусть 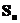- число успехов в nиспытаниях по схеме Бернулли с вероятностью успеха p.Тогда

Доказательство.

Доказательство завершено.

Таким образом, для доказательства слабой сходимости достаточно доказать сходимость по вероятности или в среднеквадратическом.

При доказательстве теорем о слабой сходимости используется также следующая важная теорема.

Теорема ({Хелли-Брея).

Пусть

и

- непрерывная ограниченная функция. Тогда

.

Доказательство.

Любую непрерывную на всей прямой функцию можно сколь угодно точно приблизить линейной комбинацией ступенчатых функций на любом интервале [-A,A) , A>0.

Выберем A так, чтобы точки –A, A и точки разбиения

были бы точками непрерывности функции распределения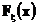

Тогда интегралы

одинаковым образом выражаются через значения функций распределения и 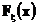и могут быть сделаны сколь угодно близкими выбором достаточно большого n. Следовательно, близки и интегралы

Так как функция ограничена, то выбором достаточно большого A можно сделать сколь угодно малыми интегралы

Теорема доказана.

Верна и обратная теорема.

Теорема (Обратная теорема Хелли-Брея)

Пусть для любой

непрерывной ограниченной функции

Тогда

Доказательство.

Идея доказательства аналогична идее доказательства предыдущей теоремы и основана на возможности приблизить ступенчатую функцию непрерывной функцией . Действительно, опять выбирая подходящие точки непрерывности и полагая

видим, что близкие между собой интегралы

можно сделать сколь угодно близкими, соответственно. к интегралам

Теорема доказана.

Так как

,

то последние две теоремы дают необходимые и достаточные условия слабой сходимости в терминах сходимости математических ожиданий от непрерывных ограниченных функций.

Теорема (f(W)).

Пусть

и

- непрерывная функция. Тогда

.

Доказательство.

Так как подстановка непрерывной функции в ограниченную непрерывную функцию приводит снова к непрерывной ограниченной функции, то доказательство этой теоремы напрямую следует из теорем Хелли-Брея.

Теорема доказана.

Нетрудно показать, что верна также следующая теорема

Теорема (f(P)).

Пусть

и

- непрерывная функция. Тогда

.

Доказательство этой и следующих двух теорем проведите самостоятельно в качестве упражнений.

Теорема (W+P->W).

Пусть

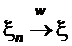
и

Тогда

Теорема (W*P->W).

Пусть

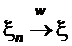
и

Тогда

Теорема Шеффе

Следующая теорема показывает, что из поточечной сходимости плотностей следует сходимость соответствующих им мер по вариации

Теорема Шеффе

Пусть - вероятностные меры, абсолютно непрерывные относительно меры 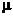и - соответствующие плотности мер относительно меры

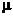
Тогда, если , то

Доказательствоэтой теоремы проведите самостоятельно по схеме доказательства соответствующего утверждения в теореме Пуассона с использованием теоремы Лебега о мажорированной сходимости.

Сглаживание распределений

Примером последовательности случайных величин, сходящихся в среднеквадратическом к нулю является последовательность

Так как

,

то для любой случайной величины 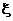и, следовательно, во всех точках непрерывности функции распределения 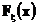. Так как , нормальное распределение имеет плотность, то случайная величина тоже имеет плотность даже для разрывной функции распределения 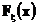и ее функция распределения при больших n является гладким приближением функции распределения .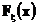