Введение в теорию вероятностей
Теория вероятностей
Введение в теорию вероятностей
Предмет теории вероятностей
| Математическая модель - это средство описания объектов и процессов реального мира в математических терминах, с помощью первичных, возможно неопределяемых, символических объектов (точка, множество ...) и строго определяемых отношений между ними (функция, оператор...). | Теория вероятностей – это математическая дисциплина, изучающая математические модели случайных явлений. Предметом теории вероятностей является математический аппарат для построения и анализа математических моделей случайных явлений, возникающих в науке, технике, экономике, бизнесе и повседневной деятельности людей. |
Возникновение и развитие теории вероятностей
До появления аксиоматики Колмогорова
Развитие теории вероятностей как науки началось в середине XVII века в связи с расчетом шансов в азартных играх. Первые теоремы были доказаны Я.Бернуллии Муавром. В 1812 году появился первый большой трактат по теории вероятностей Лапласа. В это время теория вероятностей начинает применяться в естествознании, технике и военном деле (теория ошибок наблюдений, теория стрельбы). Во второй половине 19 века вероятностные методы уже используются в демографии, статистике и страховании. Первым российским математиком, внесшим значительный вклад в теорию вероятностей, был Чебышев, работы которого были продолжены Марковыми Ляпуновым.
В наше время
Современный период в развитии теории вероятностей начинается с работ Бернштейна, Бореляи Колмогорова. Теория вероятностей стала математической наукой в 1933 году после выхода книги Колмогорова "Основные понятия теории вероятностей", в которой предложена аксиоматика теории вероятностей. С помощью этой аксиоматики удалось объяснить многочисленные парадоксы теории вероятностей, в ее рамках теория вероятностей развивается до сих пор. Наиболее бурно развивающиеся сейчас разделы теории вероятностей это теория случайных процессов, стохастическая геометрия, статистические приложения теории вероятностей.
Необходимость теории вероятностей как науки
Теория вероятностей необходима тогда, когда требуется дать количественную оценку неопределенности, возникающей при анализе случайных явлений, предсказать наиболее вероятный исход опыта, оценить средние значения случайных факторов и отклонения от них, исследовать взаимосвязь явлений, между которыми нет жесткой зависимости. Теория вероятностей позволяет дать специальный язык для описания некоторых объектов реального мира. Методы теории вероятностей помогают анализировать большие объемы статистических данных и предлагать для них математические модели. Отказ от использования методов теории вероятностей при анализе даже простейших задач со случайными факторами или неправильное их применение может привести к значительным количественным ошибкам и ложным качественным заключениям.
Возможность анализа случайных явлений
| Случайное явление – это представитель совокупности явлений, исход каждого из которых в отдельности непредсказуем, но которые все вместе подчиняются некоей общей закономерности. | Возможность анализа случайных явлений и получения точных количественных оценок основана на существовании объективной закономерности, которой подчиняется совокупность случайных явлений, рассматриваемая в целом. Например, невозможно предсказать, какая сторона монеты выпадет при конкретном бросании, но из опыта известно, что при большом числе бросаний симметричной монеты количество гербов и решек будет приблизительно одинаково. |
Расчет шансов и прогнозирование последствий
Первые задачи на расчет вероятностей были связаны с анализом азартных игр. Знание шансов различных вариантов выпадения игральных костей может помочь в правильном определении ставок, знание вероятности появления в прикупе нужной комбинации карт может помочь принять правильное решение о выборе варианта игры. Первые ошибки в расчетах были связаны также с азартными играми.
Типичные ошибки при решении вероятностных задач без применения теории вероятностей
Ошибка Д’Аламбера
В семье из двух детей могут быть два мальчика, две девочки или мальчик и девочка. Следовательно, вероятность того, что в семье есть мальчик, равна (по Д'Аламберу) 2/3. На практике, однако, доля семей с двумя детьми, из которых один мальчик, близка к 1/2 . Почему?
Задача о днях рождения
Более половины всех типичных (24-30 студентов) студенческих групп содержат как минимум двух студентов с одинаковыми днями рождения. Опрос студентов о шансах такого совпадения дает величину вероятности порядка одной сотой - одной десятой. Почему вероятность > 0.5?
Парадокс движения автобусов
Интервал движения автобусов 10 минут. На первый взгляд кажется, что среднее время ожидания автобуса на остановке – 5 минут. Однако на практике оно больше, и может составлять те же 10 минут. Почему?
Примеры практических задач, при решении которых применяется теория вероятностей
Область практических приложений теории вероятностей очень широка и будет расширяться в дальнейшем
Примеры практических задач, при решении которых не стоит применять теорию вероятностей
В некоторых случаях теорию вероятностей лучше не применять
Игра по крупному
Если у Вас всего 1000$, то играть в игру, ставка в которой 1000$, не стоит даже, если шансы выиграть равны 60%. Если у Вас в кармане миллион, то играть в такую игру Вам чем чаще, тем выгодней.
Основные понятия и определения
Первичные понятия
Опыт (эксперимент)
Одним из важнейших этапов в построении математической модели случайного объекта или процесса является его описание в первичных терминах. В теории вероятностей принято называть это описание описанием опыта или эксперимента. Основным в этом описании является определение элементарного исхода опыта. Главная трудность при построении математической модели состоит в том, что одному случайному явлению можно сопоставить бесчисленное множество разных описаний в виде опыта и, соответственно, разных вариантов элементарных исходов.
Элементарный исход
Элементарный исход является первичным понятием, и пояснить его можно только на примере. Элементарный исход является мельчайшей неделимой единицей описания опыта, мельчайшим случайным событием. Предполагается, что у одного опыта одновременно не может произойти два разных элементарных исхода. Из разных возможных описаний опыта в теории вероятностей чаще всего имеет смысл выбрать наиболее детальное. Например,
· 1. Опыт: бросание монеты
· Элементарные исходы: герб, решка – всего два различных исхода
· 2. Опыт: бросание игральной кости
· Элементарные исходы, 1 вариант: число очков на верхней грани –6 исходов
· Элементарные исходы, 2 вариант: выпала четная или нечетная грань –2 исхода
· 3.Опыт: бросание двух игральных костей
· 3.1 Элементарные исходы, 1 вариант: выпало в сумме 6 очков или не выпало –2 исхода
· 3.2 Элементарные исходы, 2 вариант: выпало в сумме 7 очков или не выпало –2 исхода
· 3.3 Элементарные исходы, 3 вариант: сумма выпавших очков – 11 исходов
· 3.4 Элементарные исходы, 4 вариант: числа очков на костях без различения игральных костей [{1,1},{1,2},{1,3},{1,4},{1,5},{1,6},{2,2},{2,3},{2,4},{2,5},{2,6}, {3,3}…] – 21 исход
· 3.5 Элементарные исходы, 5 вариант: числа очков на костях c различением игральных костей [(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),…] –36 исходов
Определения
Подмножества
Если пространство элементарных исходов определено, то появляется возможность описать любое событие, происшедшее в опыте, просто указав, какие элементарные исходы ему соответствуют.
· Пример.3.5 Элементарные исходы, 5 вариант: числа очков на костях с различением игральных костей [(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),…] –36 исходов.
· Элементарный исход можно представить в виде
· 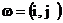 ,
,
· где i – число очков на первой кости, j – второй кости.
· Тогда событие «на двух костях выпало в сумме 7 очков» можно представить в виде следующего подмножества элементарных исходов:
· 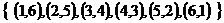
Заметим, что порядок перечисления элементарных исходов может быть произвольным. В дальнейшем подмножества пространства элементарных исходов будем обозначать большими латинскими буквами A, B, C…
A = 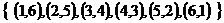
Пустое подмножество обозначим
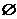
Так как пустое подмножество не содержит никаких элементарных исходов, в теории вероятностей оно обозначает невозможное событие.
Множество всех элементарных событий W называется, естественно, достоверное событие.
Элементарный исход как случайное событие представляет собой одноточечное подмножество.
Операции над подмножествами
Стандартные операции над подмножествами применяются в теории вероятностей и имеют вероятностную интерпретацию.
Дополнение
Дополнение до подмножества A - это подмножество
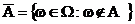
т. е. дополнением к A является подмножество, включающее в себя все элементарные исходы, не содержащиеся в A. С точки зрения теории вероятностей подмножество A представляет событие, которое естественно назвать отрицание A или не-A. Т.е. A в опыте не произошло («не наступило»).
Объединение
Объединением двух подмножеств A и B является подмножество
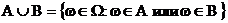
Соответственно и интерпретация : произошло или A или B.
Пересечение
Пересечением двух подмножеств : A и B является подмножество
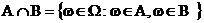
Соответственно и интерпретация : и A и B произошли одновременно.
Разность
Разностью двух подмножеств A и B является подмножество
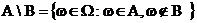
Соответственно и интерпретация : A произошло, B - нет.
Симметричная разность
Симметричной разностью двух подмножеств A и B является подмножество
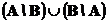
Соответственно и интерпретация : произошло только одно из этих двух событий.
Вложение
Подмножество В вложено в подмножество A, если любой элементарный исход, содержащийся в B также содержится и в A.

Интерпретация:
Стрелкой  будем пользоваться также и для утверждений типа: “из A следует B”в формулировках определений и теорем будем пользоваться также и для утверждений типа: “из A следует B”в формулировках определений и теорем | из B следует A  |
Т.е, если произошло B, то произошло и A.
Несовместность
Подмножества A и B называются несовместными (непересекающимися), если они не содержат общих элементарных исходов.

В теории вероятностей это означает, что A и B одновременно произойти не могут.
Противоположность
Подмножества A и B называются противоположными или дополнительными друг к другу, если они несовместны и их объединение достоверно.

В теории вероятностей это означает, что в опыте обязательно произойдет одно и только одно из этих событий.
Формулы
·
| Для доказательства равенства двух подмножеств A и B достаточно показать, что A вложено в B, и что B вложено в A | Следующие формулы позволяют выразить одни операции с подмножествами через другие. Доказательства проведите сами.   |
Полная группа подмножеств
Полной группой подмножеств называется конечный набор или счетная последовательность попарно несовместных подмножеств  объединение которых достоверно:
объединение которых достоверно:

В опыте обязательно произойдет одно и только одно из этих событий.
Любые два противоположных подмножества образуют полную группу подмножеств.
Если пространство элементарных исходов конечно или счетно, то сами элементарные исходы являются полной группой подмножеств.
Алгебра и сигма-алгебра
При построении математической модели случайного объекта необходимо не только указать все возможные элементарные исходы опыта, но и определить (перечислить) все возможные события, которые могут произойти в этом опыте. Принято следующее определение:
Алгебра событийAэто набор подмножеств пространства элементарных исходов  для которого выполняются следующие условия:
для которого выполняются следующие условия:

Сигма - алгебра событийFэто набор подмножеств пространства элементарных исходов  для которого выполняются следующие условия:
для которого выполняются следующие условия:

и для любой счетной последовательности

Очевидно, что любая сигма-алгебра является алгеброй, но не наоборот.
Колмогоров показал, что естественной математической моделью для множества событий является сигма-алгебра.
Очевидным примером сигма-алгебры является набор всех подмножеств пространства элементарных исходов – это наибольшая сигма-алгебра, возможная на данном пространстве элементарных исходов.
Наименьшая (тривиальная) сигма-алгебра это следующий набор подмножеств

Если алгебра или сигма-алгебра содержит событие A , то она обязана содержать и отрицание A. Поэтому минимальное число подмножеств в нетривиальной сигма-алгебре равно 4.

Алгебры и сигма-алгебры обозначаем жирными наклонными латинскими буквами.
Случайные события
Элемент сигма-алгебры в дальнейшем будем называть случайным событием.
Пересечение сигма-алгебр
| Самостоятельное доказательство этого утверждения является хорошим средством для того, чтобы понять, что такое сигма-алгебра | Пересечение двух любых сигма-алгебр, определенных на одном и том же пространстве элементарных исходов также является сигма-алгеброй. Аналогично пересечение любого (не обязательно счетного) количества сигма-алгебр, определенных на одном и том же пространстве элементарных исходов также является сигма-алгеброй. |
Минимальная сигма-алгебра
Пусть D – некоторый набор случайных событий (набор любой мощности). Пересечение всех сигма-алгебр, содержаших этот набор, называется минимальная сигма-алгебра, порожденная набором D и обозначается
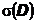
В частности, если 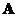 событие , то
событие , то
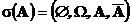
Полная группа событий
Полная группа событий это полная группа подмножеств, каждое из которых является событием. Говорят , что события полной группы это разбиение пространства элементарных исходов.
Конечно-аддитивная функция
Пусть A – алгебра. Функция n , отображающая алгебру в множество действительных чисел
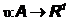
называется конечно-аддитивной, если для любого конечного набора попарно несовместных событий
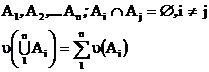
Счетно-аддитивная функция
Пусть F – алгебра или сигма-алгебра. Функция
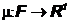
называется счетно-аддитивной, если она конечно-аддитивна и для любого счетного набора попарно несовместных событий
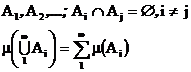
Мера
Мера - это неотрицательная счетно-аддитивная функция, определенная на сигма-алгебре, удовлетворяющая условию
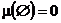
Конечная мера
Мера 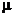 называется конечной, если
называется конечной, если 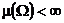
Вероятность
Вероятность (вероятностная мера) P это мера такая , что
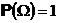
С этого момента мы перестанем измерять вероятность в процентах и начнем измерять ее действительными числами от 0 до 1.
| Когда вы пишите Pвсегда представляйте себе, какое пространство элементарных исходов и сигма-алгебра имеются в виду. Тогда вы сможете избежать многих ошибок | Обозначение P (Probability)для вероятности является стандартным, не стоит только забывать,что сама по себе (без определения пространства элементарных исходов и сигма-алгебры) вероятность не определена. |
Число
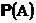
называют вероятностью события A
Вероятностное пространство
Вероятностное пространство это совокупность трех объектов – пространства элементарных исходов, сигма-алгебры событий и вероятности.
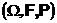
Это и есть математическая модель случайного явления или объекта.
Парадокс определения вероятностного пространства
Вернемся к исходной постановке задачи теории вероятностей. Нашей целью было построение математической модели случайного явления, которая помогла бы количественно оценить вероятности случайных событий. В то же время для построения вероятностного пространства необходимо задать вероятность, т.е. вроде бы именно то, что мы ищем (?).
Разрешение этого парадокса в том, что для полного определения вероятности как функции на всех элементах F,обычно достаточно задать ее на лишь на некоторых событиях из F, вероятность которых нам легко определить, а затем, пользуясь ее счетной аддитивностью, вычислить на любом элементе F.
Независимые события
Важным понятием теории вероятностей является независимость.
События A и B называются независимыми, если
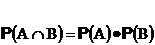
т.е. вероятность одновременного осуществления этих событий равна произведению их вероятностей.
Попарно
События в счетном или конечном наборе называются независимыми попарно, если любая пара из них является парой независимых событий
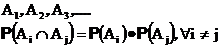
В совокупности
События в счетном или конечном наборе называются независимыми в совокупности , если вероятность одновременного осуществления любого конечного поднабора из них равна произведению вероятностей событий этого поднабора.
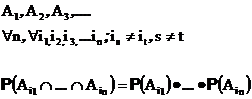
Ясно, что независимые в совокупности события независимы и попарно. Обратное неверно.
Условная вероятность
Условной вероятностью события A при условии, что произошло событие B называется величина
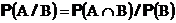
Условную вероятность пока определим лишь для событий B, вероятность которых не равна нулю.
Если события A и B независимы, то
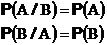
Свойства и теоремы
Формулировка.
Пусть

убывающая последовательность событий с пустым общим пересечением
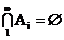
Тогда
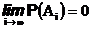 .
.
Доказательство.
Заметим, что события
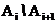
попарно несовместны и
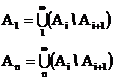
Следовательно ряд из вероятностей событий
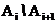
сходится и его хвост, равный
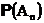
стремится к нулю.
| Докажите! | Верно и обратное – ограниченная непрерывная конечно-аддитивная функция является счетно-аддитивной. |
Заметим, что для доказательства важна только конечность значения 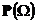 , поэтому теорема справедлива не только для вероятностных, но и для любых конечнных мер.
, поэтому теорема справедлива не только для вероятностных, но и для любых конечнных мер.
Факториал
Количество всех различных перестановок n различных чисел равно
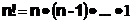
Формула Стерлинга
Для приближенного вычисления факториалов больших чисел используется формула Стирлинга
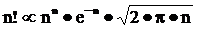
Биномиальный коэффициент
Количество двоичных векторов размерности n с ровно k единицами равно
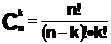
Бином Нютона
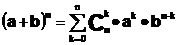
Полиномиальная формула
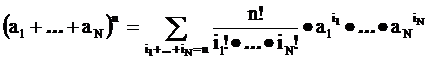
Схема выбора с возвращением
Частным случаем классической вероятностной модели является так называемая схема выбора с возвращением. Элементарный исход – это вектор
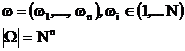
Схема является примером того, как можно строить сложные вероятностные модели из более простых. Эта схема применяется для описания ситуаций , в которых некоторый простой опыт с N возможными равновероятными исходами повторяется n раз.
Название схема получила от следующей ее интерпретации.
В урне находится N различных шаров. Из урны случайно вынимается один шар и записывается его номер
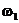
После этого шар возращается обратно в урну, и опыт поворяется снова (всего n раз).
Пример вычисления вероятности события в схеме выбора с возвращением.
Игральная кость бросается 20 раз. Найти вероятность того, что выпадет 2 единицы, 4 пятерки, 3 шестерки (событие A)
Решение.
В этом случае n=20, N=6.
| Обратите внимание, что мы не ищем сразу вероятность исходного события, а придумываем как легче выразить это событие через другие, вероятность которых легче подсчитать | Найдем вначале вероятность того, что в результате опыта выпадет i1 единиц, i2 двоек, i3 троек, i4 четверок, i5 пятерок, i6 шестерок (событие A(i1, i2 , i3 , i4, i5 , i6 )). Для этого необходимо подсчитать количество элементарных исходов, удовлетворяющих этому требованию. Используя формулы комбинаторики получаем, что искомое количество равно  Следовательно, вероятность равна Следовательно, вероятность равна 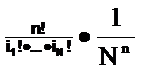 В нашем случае В нашем случае 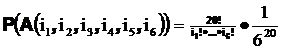 Осталось сложить вероятности всех подходящих событий и найти вероятность A Осталось сложить вероятности всех подходящих событий и найти вероятность A 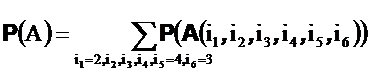 Суммирование ведется по всем возможным значениям индексов, удовлетворяющих условиям. В частности, по i1=1, по i2 от 1 до 6, по i3 от 1 до 6 и т.д. Суммирование ведется по всем возможным значениям индексов, удовлетворяющих условиям. В частности, по i1=1, по i2 от 1 до 6, по i3 от 1 до 6 и т.д. |
| Попробуйте вычислить эту вероятность. | Вычисление этой вероятности не так то просто даже при наличии компьютера. Для этого придется написать небольшую программу. |
Урновая схема
| Придумайте свою урновую схему и опишите ее в виде вероятностного пространства | Урновой схемой называется схема выбора, при которой в урне содержатся в некотором количестве шары разных цветов и после вынимания шара (или нескольких шаров) какого либо цвета в урну добавляются шары того же или иного (по некоторому правилу) цвета. Эти схемы можно использовать для описания более сложных опытов. |
Теорема Пуассона.
Пусть параметры биномиального распределения изменяются следующим образом
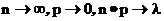
Тогда
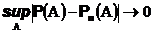
т.е. биномиальная вероятность равномерно по всем случайным событиям стремится к пуассоновской вероятности.
Доказательство.
Докажем вначале, что в условиях теоремы для любого фиксированного k
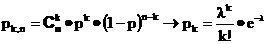
Действительно, сгруппировав множители входящие в pk,n следующим образом
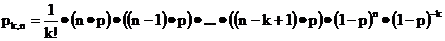 получим
получим
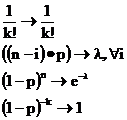
Покажем теперь, что из сходимости
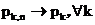
следует
сходимость
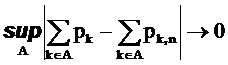
Действительно, определив множество A* следующим образом
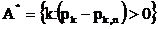
получим
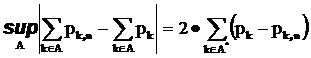
Далее, так как на множестве A*
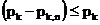
для любого N получаем
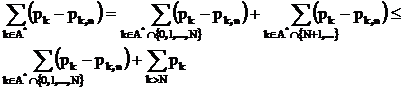
Выбрав N достаточно большим, можно сделать вторую сумму сколь угодно малой, первую сумму после этого можно сделать также сколь угодно малой выбрав достаточно большое n.
Доказательство завершено.
При больших k рассчитать пуассоновскую вероятность гораздо легче, биномиальную. Пуассоновское распределение используется для приближения биномиального распределения в тех случаях, когда количество испытаний в схеме Бернулли велико, а вероятность успеха мала.
Сходимость по вариации.
Последовательность вероятностей (вероятностных мер или их распределений) Pn сходится к вероятности (распределению) P по вариации, если
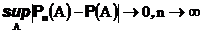
В предыдущем пункте мы доказали сходимость по вариации биномиальной вероятности к пуассоновской (в некоторых условиях).
Измеримое пространство.
В предыдущем пункте мы определили две различные вероятности на одной и той же сигма-алгебре событий. В дальнейшем нам придется делать это неодократно. Для удобства дадим следующее определение.
Измеримое пространство – это пара
Независимость
Различие между независимостью попарно и в совокупности. Пример Бернштейна
Данный пример показывает, что существуют попарно независимые события , которые не являются независимыми в совокупности.
Рассмотрим тетраэдр, грани которого покрашены в три цвета следующим образом:
1 грань – синяя
2 грань – зеленая
3 грань – желтая
4 грань разделена на три сектора – синий, зеленый и желтый.
Опыт состоит в бросании тетраэдра и наблюдении цвета выпавшей (нижней) грани.
Обозначим события
A – на грани есть синий цвет
B – на грани есть зеленый цвет
C – на грани есть желтый цвет
Тогда, используя симетричность тетраэдра и классическую вероятностную модель получим:
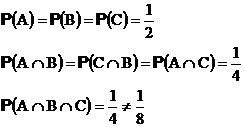
Для исключения неоднозначности при интерпретации понятия независимости в теории вероятностей при построении моделей используется, в основном, независимость в совокупности, как более сильная. В дальнейшем говоря о независимости мы, если не указано противное, будем подразумевать независимость в совокупности.
Примеры построения моделей.
Ранее были рассмотрены два примера построения моделей с использованием понятия независимости – схема Бернулли и мультиномиальная схема. Приведем еще несколько примеров.
Условная вероятность
Часто случайные компоненты в опыте и соответственно координаты элементарного исхода являются зависимыми. В этом случае для определения распределения используют понятие условной вероятности.
Урновая схема
Рассмотрим, например, эксперимент, описывающий выбор двух шаров из урны, содержащей 20 черных и 10 белых шаров, без возвращения. Элементарным исходом будет вектор
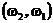
из нулей и единиц (1 – черный шар, 0 - белый), где первая координата описывает цвет второго извлеченного шара, а вторая цвет первого извлеченного шара.
Как задать вероятность элементарного исхода?
Ясно, что событие «На первом шаге вынут черный шар» должно иметь вероятность
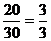
Ясно также, что если бы мы знали цвет извлеченного на первом шаге шара, то точно также могли бы определить вероятность извлечения черного шара на втором шаге. Именно, если первый шар белый, то (при этом условии) вероятность извлечь черный шар на втором шаге равна
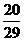
Если первый шар черный, то
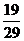
Тогда естественно определить вероятность исхода (1,1) так чтобы выполнялась формула условной вероятности
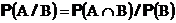
т.е.
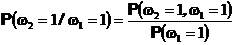
и
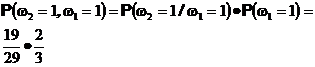
Аналогично определяются вероятности остальных элементарных исходов
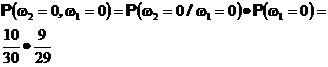
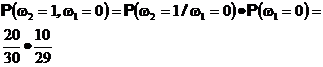
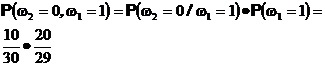
Теперь нетрудно, например, вычислить вероятность того, что второй извлеченный шар будет черным. Она равна
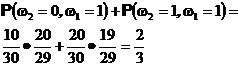
| Покажите, что нас самом деле вероятность вытащить черный шар одинакова не только для первого и второго, но и для любого другого шага выбора (пока она не станет равной, естественно, нулю – когда кончатся черные шары) | Заметим, что данный результат в применении к задаче о студенте на экзамене означает, что студенту все равно каким идти – первым или вторым. |
Марковская зависимость
Легко распространить изложенное выше на случай элементарного исхода с n целочисленными координатами.
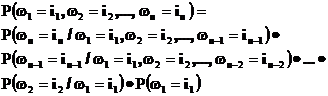
Особенно просто записывается вероятность элементарного исхода когда имеет место марковская зависимость координат, т.е. когда распределение следующей координаты зависит только от значения предыдущей координаты
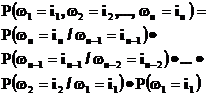
В этом случае последовательные переходы от координаты 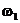 к координате
к координате 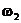 и т.д. называются шагами ,а вероятности
и т.д. называются шагами ,а вероятности
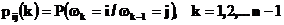
называются переходными вероятностями (за один шаг).
Если каждая координата вектора 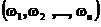 принимает значения в одном и том же конечном множестве
принимает значения в одном и том же конечном множестве 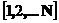 (множестве состояний) и переходные вероятности не зависят от n,топоследовательность
(множестве состояний) и переходные вероятности не зависят от n,топоследовательность 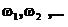 называется конечной цепью Маркова. В этом случае вероятность элементарного исхода можно записать так
называется конечной цепью Маркова. В этом случае вероятность элементарного исхода можно записать так
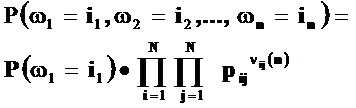
где
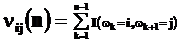
- количество переходов из состояния i в состояние j
Подробно марковские зависимости исследуются в теории случайных процессов.
Случайные величины
В данной главе рассматриваются отображения одного вероятностного пространства в другое. Важнейшим случаем такого отображения является отображение основного пространства в пространство действительных чисел или векторов. Возникающие при этом случайные величины, случайные вектора и их распределения являются одними из основных понятий теории вероятностей.
Случайная величина
Случайной величиной называется измеримое отображение основного вероятностного пространства в множество действительных чисел. С практической точки зрения случайная величина это числовая характеристика эксперимента. Чтобы дать корректное определение случайной величины, необходимо указать подходящую сигма-алгебру на пространстве действительных чисел. В дальнейшем пространство действительных чисел будем обозначать

а пространство векторов с n действительными координатами

Борелевская сигма-алгебра
Так как сигма-алгебра на пространстве действительных чисел нужна нам для того, чтобы определить на ней вероятность, то естественно включить в эту сигма-алгебру побольше практически важных множеств. Обозначим

минимальную сигма-алгебру, содержащую всевозможные интервалы вида
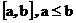
Эта сигма-алгебра называется борелевская сигма-алгебра (Борель Эмиль). Она содержит все практически важные множества действительной прямой. Множество, принадлежащее борелевской сигма-алгебре называется борелевское множество.
Точка
Очевидно, что любая точка это замкнутый интервал с одинаковыми концами
Открытый интервал
Покажем, что любой открытый интервал содержится в борелевской сигма- алгебре. Действительно, из определения сигма-алгебры следует, что вместе с каждой парой множеств A, B сигма-алгебра содержит пересечение, объединение и, следовательно, разность этих множеств.
Осталось заметить,что

Полуось

Другие множества
Пусть
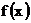
непрерывная функция.
Тогда множества
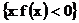 ,
, 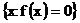 ,
, 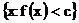 ,….
,….
являются борелевскими.
Неборелевские множества
Таким образом, можно привести массу примеров практически важных борелевских множеств. Возникает вопрос: может быть все множества на прямой борелевские?
Обозначим
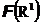
наибольшую сигма-алгебру, т.е. сигма-алгебру, включающую в себя все подмножества действительных чисел
Тогда, очевидно, что
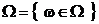
Но, оказывается, что
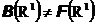
Доказательство этого утверждения (пример неборелевского множества на действительной прямой) содержится в курсе функционального анализа.
Варианты определения борелевской сигма-алгебры
Борелевская сигма-алгебра определена как минимальная сигма-алгебра, содержащая все интервалы вида
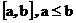
т.е.
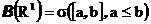
Ясно, теперь, что
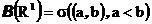
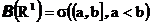
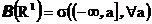
и т.д.
Доказательство.
Необходимость очевидна.
Множества E такие, ч
