Расчет статически неопределимых систем методом сил

Алгоритм расчета статически неопределимой системы в строймехе методом сил:

1. Расчет степени статической неопределимости:

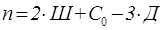
2. Выбор основной системы (исключается "лишняя" связь).

3. Запись системы канонических уравнений.

4. Построение эпюр от сил, равных 1 и эпюры от заданной внешней нагрузки.

5. Определение коэффициентов канонических уравнений.

6. Проверка найденных коэффициентов канонических уравнений.

7. Полученная система уравнений решается матричным способом.

8. Строятся эпюры внутренних усилий (M, Q, N).

Способ Верещагинапри перемножении эпюр:

Интеграл перемножения двух функций, ограничивающих эпюры, причем одна из которых представляет собой прямую линию, а другая является криволинейной, равен произведению площади фигуры криволинейной эпюры, на ординату из эпюры, ограниченной прямой линией, которую берут под центром тяжести площади эпюры, ограниченной произвольной линией.

Если фигуры эпюр представляют собой прямоугольные треугольники:

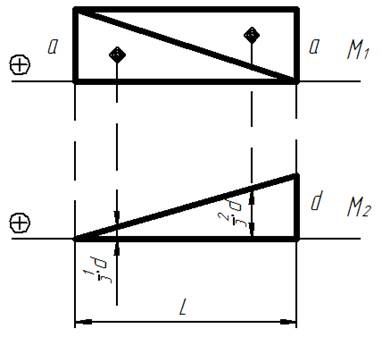
Перемножение эпюр, представляющих собой треугольники

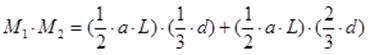
Если фигуры эпюр представляют собой трапеции:

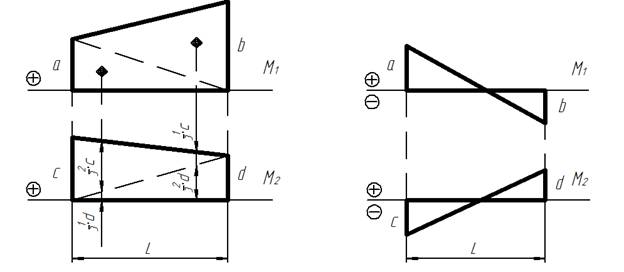
Перемножение эпюр, представляющих собой трапеции

Формула для трапеций применима и когда эпюры представлены в виде треугольников – поскольку треугольник можно представить как трапецию с одной из сторон, равной нулю.

Если одна из фигур эпюр представляют собой выпуклую фигуру (а) или вогнутую фигуру (б):

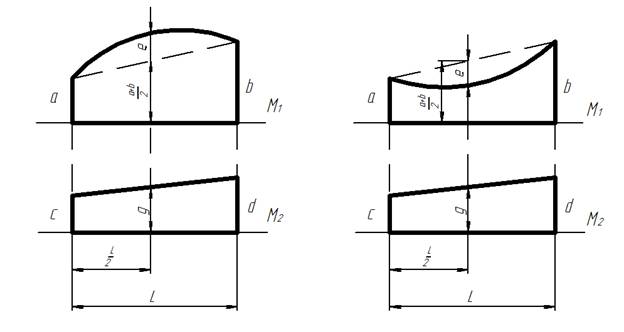
Перемножение прямолинейной и криволинейной эпюр

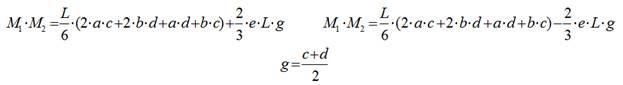
Когда ни одна из эпюр не ограничена одной прямой линией, но одна из них или ограничена несколькими прямыми линиями, как на рисунке ниже, то в этом случае эти эпюры разбивают на отдельные участки, так, что на каждом из них эпюры ограничены одной прямой линией:

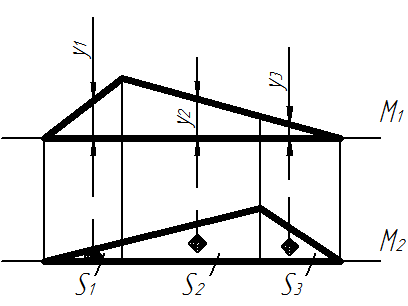
Перемножение сложных прямолинейных фигур

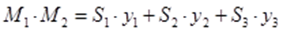
Произведение ординат эпюр, расположенных по одну сторону от нулевой линии, берется со знаком «+», по разные стороны – со знаком «–».

С. Задача

Построить эпюры внутренних усилий для статически неопределимой системы методом сил.

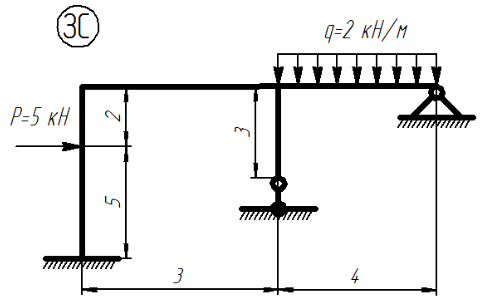
Статически неопределимая система

1) Определяем степень статической неопределимости системы и строим основную систему:

1.1) Определяем степень статической неопределимости системы:

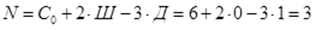
1.2) Выбираем основную систему (ОС):

Возможные следующие варианты основной системы:

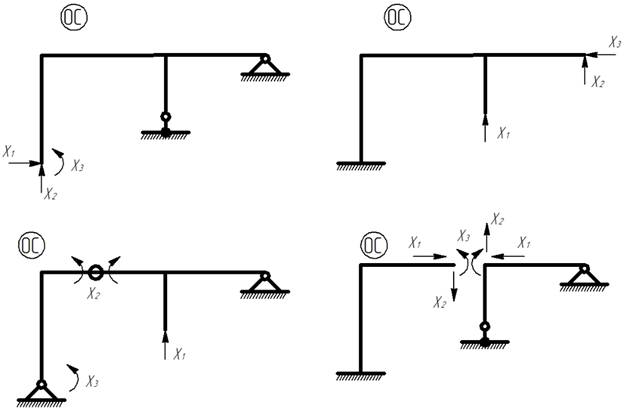
Варианты основной системы

Выбираем наиболее простую для построения эпюр изгибающих моментов:

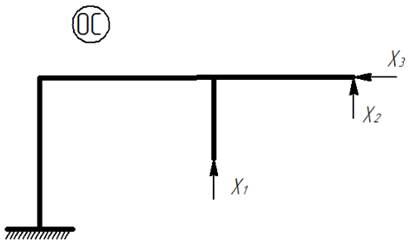
Основная система для расчета методом сил

2) Составляем систему канонических уравнений:

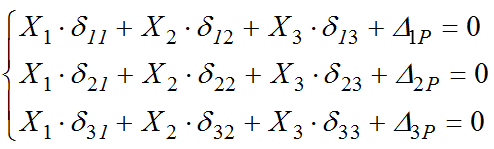
3) Строим эпюру Мр (грузовую эпюру):

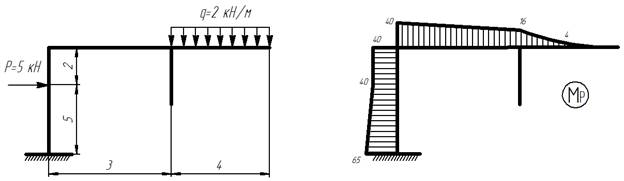
Грузовая эпюра

4) Строим эпюры изгибающих моментов от единичных сил:

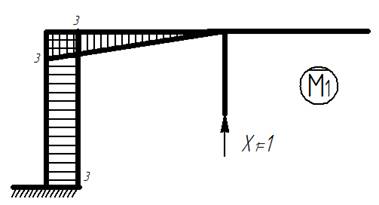
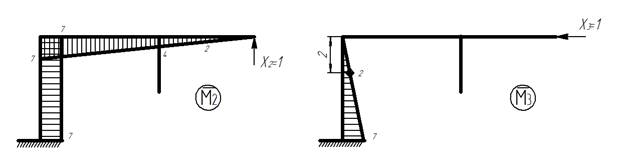
Единичные эпюры

5) Определяем главные коэффициенты:

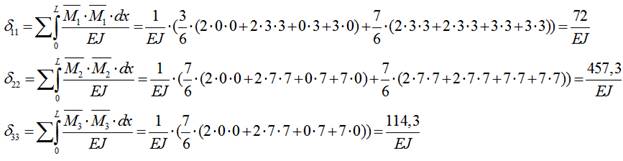
6) Определяем боковые коэффициенты:

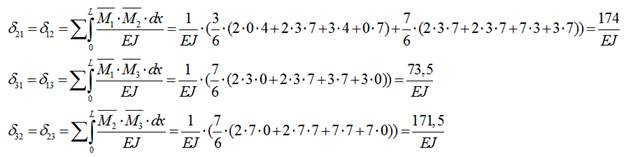
7) Определяем свободные коэффициенты:

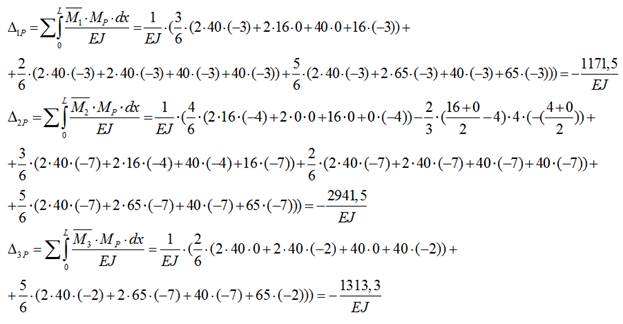
8) Проверяем коэффициенты канонических уравнений:

8.1) Строим суммарную единичную эпюру изгибающих моментов:

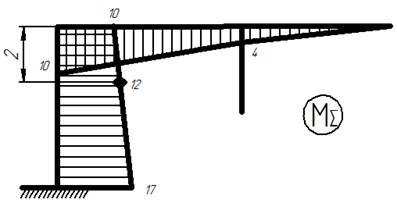
Суммарная единичная эпюра изгибающих моментов

8.2) Проверяем главные и боковые коэффициенты:

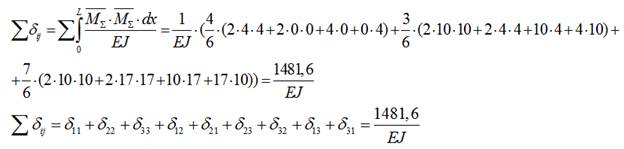
8.3) Проверяем свободные коэффициенты:

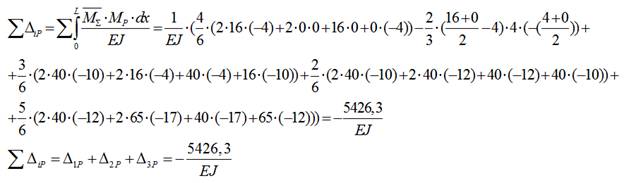
9) Преобразуем систему канонических уравнений:

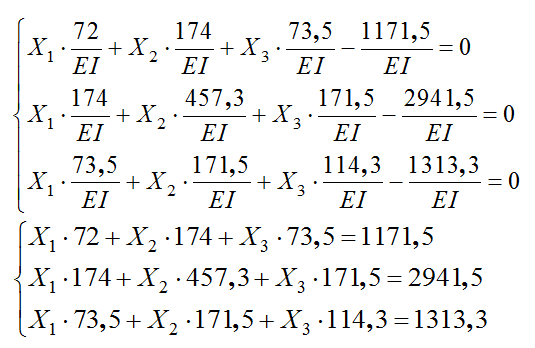
10) Решаем систему канонических уравнений матричным методом:

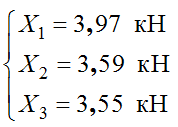
11) Умножаем каждую единичную эпюру на соответствующее значение силы X

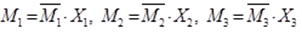
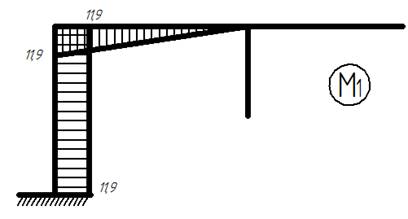
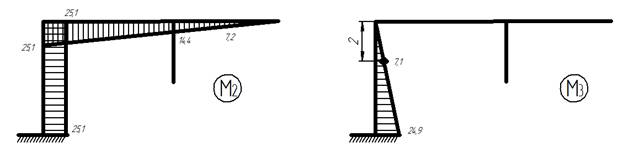
Эпюры изгибающих моментов от искомых усилий

12) Строим итоговую эпюру М= М₁+М₂+М₃+Мр:

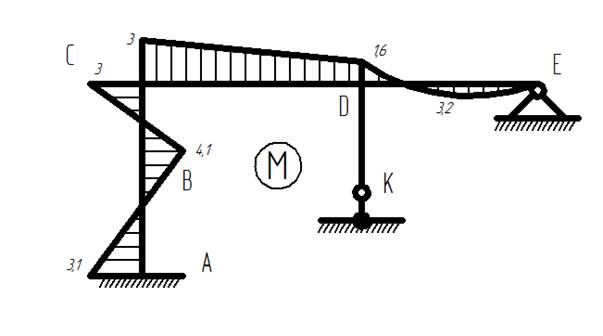
Итоговая эпюра изгибающих моментов

13) Строим эпюры поперечных сил (Q) и продольных сил (N):

I способ:

I.1) Строим эпюру Q:

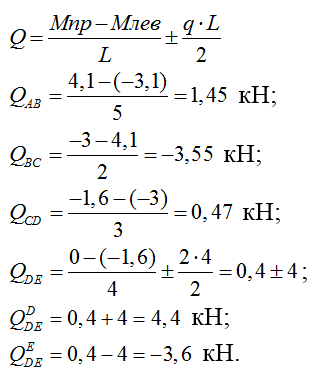
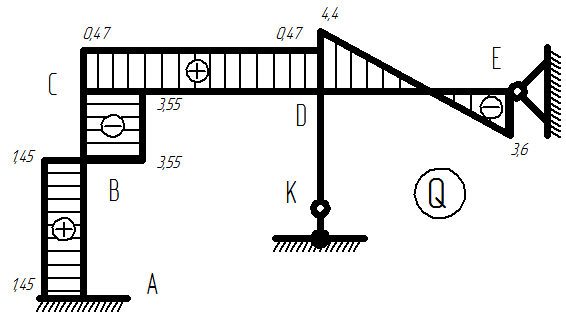
Эпюра поперечных сил

I.2) Строим эпюру N:

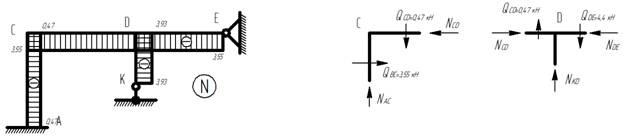
Эпюра продольных сил

II способ:

II.1) Строим эпюры – грузовую Q_P и единичные:

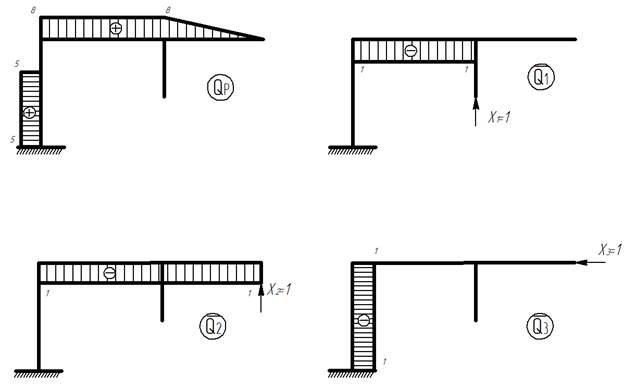
Эпюры поперечных сил

II.2) Умножаем каждую единичную эпюру на соответствующее значение силы X

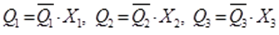
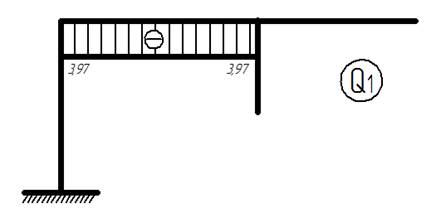
Эпюры поперечных сил

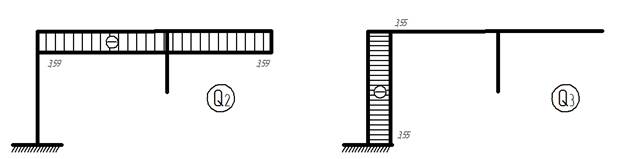
II.3) Строим итоговую эпюру Q= Q₁+Q₂+Q₃+Qр:

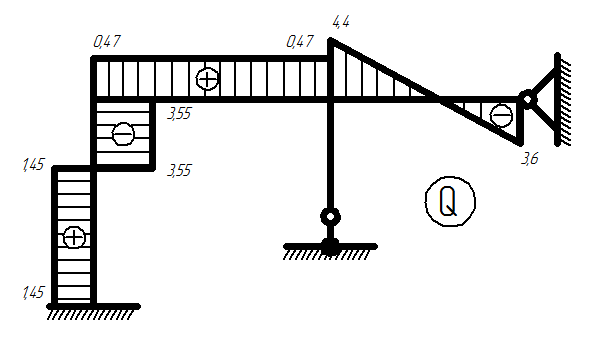
Итоговая эпюра поперечных сил

II.4) По аналогии с эпюрой Q строим эпюру N:

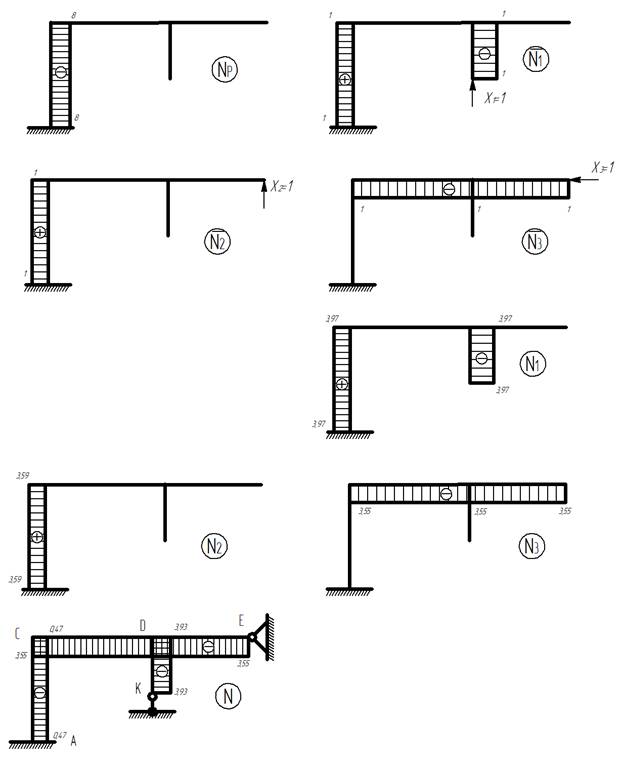
Эпюры продольных сил

III способ:

III.1) Подставив вместо неизвестных реакций найденные силы X₁, X₂, X₃ получаем статически определимую систему:

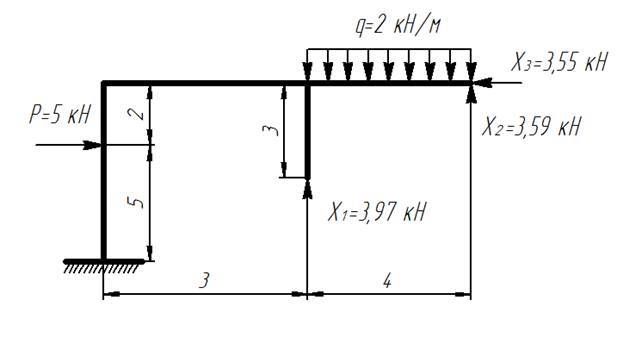
Статически определимая система

III.2) Решив ее можем построить эпюры M, Q, N как для статически определимой системы.