Мгновенный центр скоростей и ускорений

Мгновенный центр скоростей

Пользуясь теоремой о скоростях точек плоской фигуры, покажем, что в каждый момент времени существует точка, неизменно связанная с плоской фигурой, скорость которой в этот момент равна нулю. Эту точку называют мгновенным центром скоростей.

Допустим, что известны скорость некоторой точки О плоской фигуры 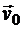(рис. 12.1) и угловая скорость фигуры 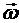в некоторый момент времени. Примем точку О за полюс. Тогда скорость любой точки фигуры будет равна геометрической сумме скорости полюса 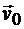и вращательной скорости точки вокруг этого полюса. Восставим в точке О перпен­дикуляр к скорости 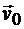так, чтобы направление поворота скорости 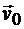к этому перпендикуляру совпадало с направлением вращения фигуры.

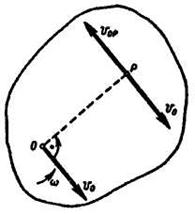
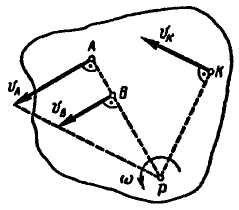
Рис. 12.1 Рис. 12.2

Вращательные скорости всех точек этого перпендикуляра вокруг полюса О направлены противоположно скорости полюса.

Найдем такую точку Р, вращательная скорость которой равна по модулю скорости полюса 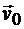, т.е. .

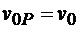Так как направления этих скоростей противоположны, то 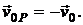Скорость точки Р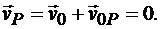

Следовательно, точка Р в рассматриваемый момент времени является мгновенным центром скоростей.

Определим положение точки Р. Вычислим вращательную скорость точки Р вокруг полюса О и приравняем ее скорости полюса:

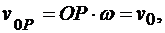
откуда

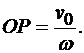(12.1)

Следовательно, мгновенный центр скоростей плоской фигуры на­ходится на перпендикуляре к направлению скорости полюса на рас­стоянии от полюса, равном .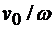

Определение скоростей точек плоской фигуры с помощью мгновенного центра скоростей.Определим скорости точек А, В и К плоской фигуры (рис. 12.2), приняв за полюс мгновенный центр скоростей Р. По формуле получим:

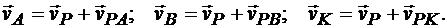
Но скорость точки Р в данный момент равна нулю, т. е. 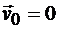. Тогда скорости точек определяются по формулам

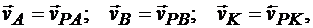(12.2)

т. е. скорость любой точки плоской фигуры в данный момент времени представляет собой вращательную скорость этой точки вокруг мгновенного центра скоростей; поэтому

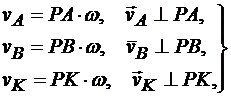(12.3)

т. е. скорость любой точки плоской фигуры в каждый момент времени имеет модуль, равный произведению угловой скорости фигуры на длину отрезка, соединяющего точку с мгновенным центром скоростей, и направлена перпендикулярно этому отрезку в сторону вращения фигуры.

Найдем зависимость между скоростями точек плоской фигуры в рассматриваемый момент времени:

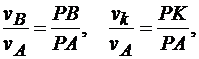
т. е. модули скоростей точек плоской фигуры в каждый момент вре­мени пропорциональны расстояниям от этих точек до мгновенного центра скоростей.

Чтобы определить скорости точек плоской фигуры с помощью мгновенного центра скоростей, необходимо знать положение мгновен­ного центра скоростей и угловую скорость фигуры.

2 частные случаи определения мгновенного

Центра скоростей

1. Допустим, что известны прямые, по которым направлены скорости двух точек плоской фигуры А и В (рис. 12.3). Тогда мгновенный центр скоростей фигуры определится как точка пересечения перпендикуляров к этим прямым, восставленных в точках А и В. Зная модуль скорости точки А и определив расстояние этой точки от мгновенного центра скоростей РА, находим угловую скорость плоской фигуры согласно зависимости (12.3):

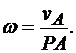
Модуль скорости точки В можно определить из пропорциональ­ности скоростей точек их расстояниям от мгновенного центра ско­ростей по формуле :

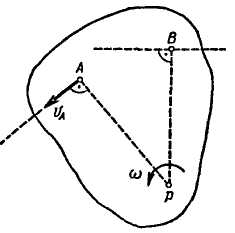
Рис. 12.3

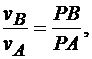
откуда

.

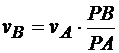или с помощью угловой скорости фигуры согласно (12.3)

.

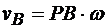Скорость любой другой точки плоской фигуры определяется ана­логично.

2. Если скорости точек А и В плоской фигуры параллельны между собой и перпендикулярны АВ, то для определения положения мгно­венного центра скоростей должны быть известны модули скоростей обеих точек А и В (рис. 12.4, а, б).

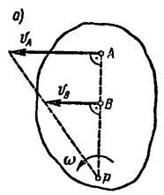
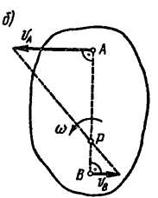
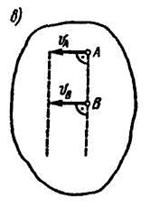
Рис. 12.4

Известно, что модули скоростей точек фигуры пропорциональны их расстояниям от мгновенного центра скоростей, т. е.

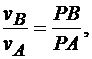
Следовательно, концы скоростей точек А и В лежат на прямой, проходящей через мгновенный центр скоростей. Пересечение этой пря­мой с прямой АВ определяет мгновенный центр скоростей фигуры.

Если скорости точек А и В плоской фигуры равны, параллельны между собой и перпендикулярны АВ, то мгновенный центр скоростей находится в бесконечности (АР = ∞), а угловая скорость фигуры (рис. 12.4, в)

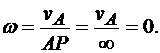
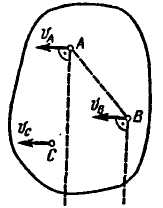
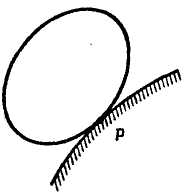
Рис. 12.5 Рис. 12.6

3. Если известно, что скорости двух точек А и В плоской фигуры параллельны и не перпендикулярны АВ (рис. 12.5), то мгновенный центр скоростей находится в бесконечности (АР = ∞). Очевидно, что и в этом случае

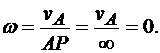
Расстояния от всех точек плоской фигуры до мгновенного центра скоростей в этом случае равны между собой:

АР=ВР=…=∞.

Поэтому скорости точек плоской фигуры в рассматриваемый мо­мент геометрически равны:

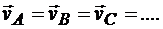
Следует учесть то, что при поступательном движении плоской фигуры скорости всех ее точек в каждый момент также геометрически равны и мгновенный центр скоростей этой фигуры находится в беско­нечности.

Если условие 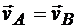остается справедливым в течение некоторого промежутка времени, а не только в отдельный момент, то движение плоской фигуры является поступательным. Если же 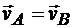только в некоторый момент времени, то утверждать, что плоская фигура движется поступательно, нельзя.

4. На практике часто происходит движение плоской фигуры, при котором она катится без скольжения по некоторой неподвижной линии (рис. 12.6). В этом случае мгновенный центр скоростей плоской фигуры находится в точке соприкасания с линией. Действительно, при отсутствии скольжения скорость точки соприкасания плоской фигуры по отношению к неподвижной кривой равна нулю, т. е. эта точка в данный момент является мгновенным центром скоростей.

Пример 1. Колесо радиусом R катится без скольжения по прямому рельсу. Скорость центра колеса в рассматриваемые момент временя 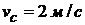. Определить скорости точек А, В, D и Е колеса, расположенных на концах взаимно перпендикулярных диаметров (рис. 12.7, а).

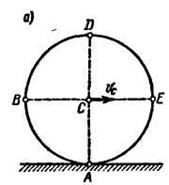
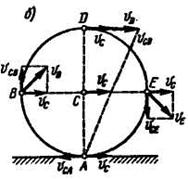
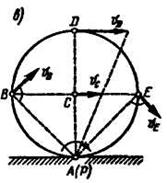
Рис. 12.7

Решение. 1-й вариант. Примем за полюс центр колеса С (рис. 12.7, б). Тогда скорость любой точки колеса будет равна геометрической сумме скорости полюса и скорости вращения этой точки вокруг полюса. Так как колесо катится без скольжения, то скорость точки А касания колеса с рельсом равна нулю: 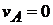. Точка А является мгновенным центром скоростей. В этой точке скорость вращения вокруг полюса 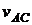и скорость полюса 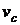равны по модулю и противоположны по направлению:

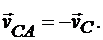
Расстояния от точек А, В, D, Е до полюса С равны. Следовательно, и вращательные скорости точек вокруг полюса тоже равны:

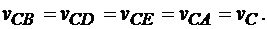
Откладывая в каждой точке скорость полюса С и вращательную скорость, перпендикулярную соответствующему радиусу, складываем их геометрически, и затем находим модуля скоростей точек:

.

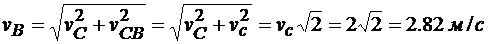2-й вариант. Примем мгновенный центр скоростей колеса за полюс. Тогда скорости всех точек колеса определяются как вращательные скорости вокруг мгновенного центра скоростей. Модуля скоростей всех точек найдутся по пропорциональности скоростей их расстояниям от мгновенного центра скоростей:

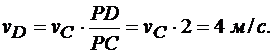
Так как 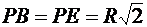, то

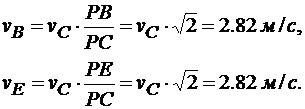
Найденные скорости точек направлены перпендикулярно соответствующим отрезкам в сторону вращения колеса (рис. 12.7, в).

Аналогичное распределение скоростей имеет место при качении колеса без скольжения по любой поверхности.

Мгновенный центр ускорений

Мгновенный центр ускорений (МЦУ) — это точка в плоско­сти движения плоской фигуры, ускорение которой равно ну­лю.

Для построения МЦУ 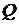при известном ускорении точки А пло­ской фигуры 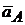, которую примем за полюс, угловой скорости 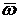и угловом ускорении 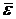необходимо (рис. 12.8):

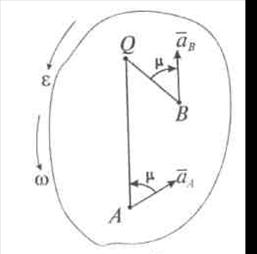
Рис. 12.8

1. Определить угол 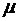по формуле: .

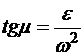2. Повернуть вектор ускорения полюса на угол 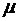, в направле­нии углового ускорения.

3. Отложить отрезок AQ :

, .

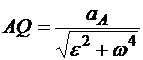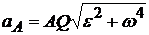по направлению повернутого вектора ускорения .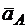

С помощью МЦУ можно найти ускоре­ние любой точки. Найдем вели­чину ускорения точки В по зависимости:

.

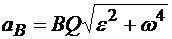От отрезка BQ под углом 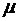откладываем в направлении, противоположном угловому ускорению, вектор ускорения точки В (рис. 12.8). МЦУ и МЦС в общем случае — раз­ные точки.

Таким образом, модули ускорений точек плоской фигуры в каждый момент времени пропорциональны расстояниям от этих точек до мгновенного центра ускорений, а векторы ускорений составляют с от­резками, соединяющими эти точки с мгновенным центром ускорений, один и тот же угол .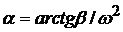

Eсли мгновенный центр ускорений принять за полюс, то ускорение любой точки плоской фигуры в данный момент определится как ускорение этой точки во вращательном дви­жении фигуры вокруг мгновенного цент­ра ускорений (рис. 12.9).

Действительно, приняв за полюс мгновенный центр ускорений Q (рис. 12.9), получим

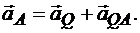
Так как

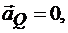
то

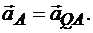
Аналогично,

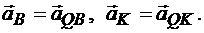
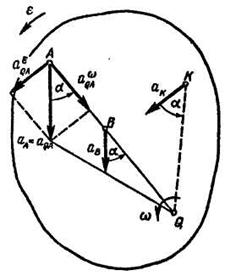
Рис. 12.9

Из этих соотношений получаем

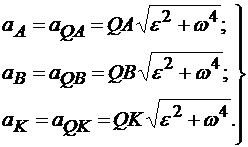(12.4)

Поэтому

.

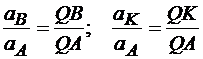Пример 2.Колесо радиуса R = 0,5 м катится без скольжения равнозамедленно по прямолинейному горизонтальному рельсу. Скорость центра колеса 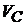= 0,5 м/с. Ускорение центра 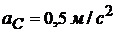. Найти ускорение точки А с помощью МЦУ и по теореме об ус­корениях точек плоской фигуры (рис. 12.10).

Решение. Находим угловые скорость и ускорение колеса:

,

.

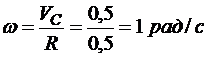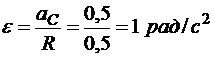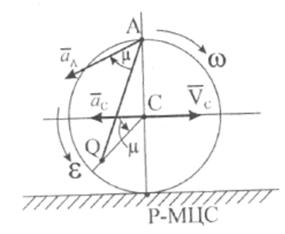
Рис. 12.10

Угловая скорость направлена по часовой стрелке, так как вектор скорости 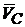относительно МЦС поворачивается по часо­вой стрелке. Угловое ускорение направлено противоположно в со­ответствии с направлением вектора ускорения центра колеса .

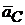I способ. Определим угол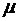

.

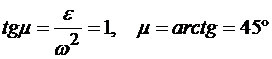Повернем 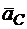на угол 45° по направ­лению углового ускорения. Определим расстояние от точки С до МЦУ (рис. 12.10):

.

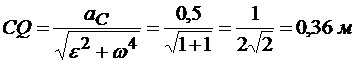Находим расстояние точки А до МЦУ из :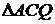

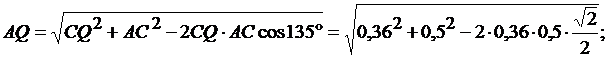
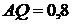м.

В точке А от отрезка AQ отложим вектор ускорения точки А в направлении, противоположном угловому ускорению. Величи­на 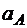ускорения точки А равна:

.

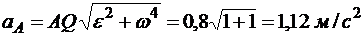II способ. Применим формулу, приняв за полюс точку С:

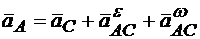. (12.5)

Находим , :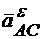

,

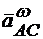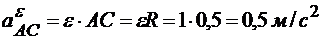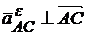и направлен в соответствии с угловым ускорением (рис. 12.11):

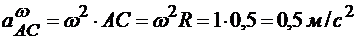
Вектор 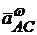направлен от точки А к полюсу С (рис. 12.11).

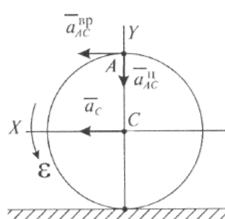
Рис. 12.11

Проецируем выражение (12.5) на выбранные оси координат:

,

,

.

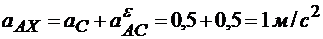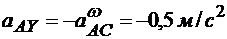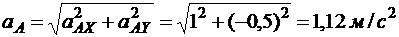Ответ. 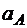=1,12 м/с².

Различные случаи определения положения мгновенного центра ускорений.Все задачи на определение положения мгновенного центра уско­рений плоской фигуры можно свести к трем указанным ниже основ­ным случаям, каждому из которых, очевидно, соответствует ряд частных случаев, зависящих от характера движения плоской фигуры.

С л у ч а й I. По условию задачи известна точка плоской фигуры, ускорение которой в данный момент равно нулю. Эта точка и является мгновенным центром ускорений.

Рассмотрим, например, качение без скольжения колеса по прямолинейному рельсу с постоянной скоростью центра 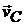(рис. 12.12).

Мгновенный центр скоростей Р находится в точке соприкасания колеса с рельсом. Поэтому

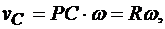
где R - радиус колеса.