Показатели центра распределения (мода, медиана, среднее арифметическое, среднее гармоническое, среднее геометрическое)

Любой многоэлементный объект, как правило оценивают небольшим числом параметров. Для описания часто используется описание центра (напр физики используют понятие центра тяжести, а геом используют понятие центра симметрии).

В статистике используют следующие показатели центра распределения: мода, медиана и среднее арифметическое.

Мода-значение признака, которое в выборке имеет наибольшую частоту.

Варианты
частоты

М=21 (мода-21)

Если дискретный признак представлен в виде полигона, то модой является варианта, в которой полигон имеет вершину. Дискретный признак может иметь одну моду, тогда он называется унимодальным.

Дискретный признак может иметь 2 моды, тогда он назыв. Бимодальным (полигон имеет 2 вершины). Признак может вообще не иметь моды, в этом случае более 2-х значений имеют одинаковую наибольшую частоту. Если признак непрерывный, то мода вычисляется:

Пусть дан непрерывный признак интервальным рядом вида:

Интерв	6,5-7,5	7,5-8,5	8,5-9,5	9,5-10,5	10,5-11,5
частоты

Пусть 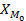-начало интервала с максимальной частотой 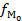. Частота на предыдущем интервале f(-), частота на последующем интервале f(+), тогда

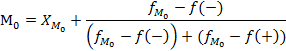
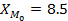, f(-)=12 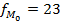, f(+)=14, тогда

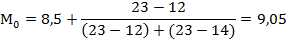
Можно найти моду графически по гистограмме :

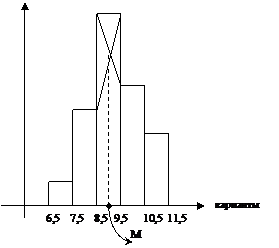
Медиана-число, которое на числовой оси делит все измеряемые значения признака на 2 равные по кол-ву группы: одни наблюдения не больше этого числа, другие –не меньше. Медиана обозначается буквами Ме. Для дискретных признаков медиана находится по следующим правилам:

· Все наблюдения (с повторениями значений, если они есть), выстраивают в порядке возрастания. Вычисляется число 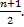Если объем выборки n-число нечетное, то это число конкретное и является номером члена в упорядоченной выборке.

n=9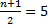

2,5,6,6,8,10,13,14,16, тогда медиана 8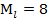

Если объем выборки –число четное, то 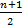–это дробное число. За медиана берут полусумму двух соседних значений.

Напр, если выборка 3,5,5,7,10,11,15,17 n=8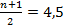

Медиана есть полусумма 4-ого и 5-ого значения , т.е.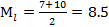

Повторения в ряду наблюдений могут попасть в середину выборки, что не меняет правил подсчета:

1,2,4,4,4,7,9 n=7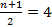

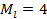
3,5,8,8,8,10,11,15 n=8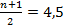

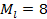
Для непрерывных признаков медиана считается с помощью интервального и кумулятивного рядов. Пусть дан интервальный вариационный ряд и одновременно построен кумулятивный.

Интерв	6,5-7,5	7,5-8,5	8,5-9,5	9,5-10,5	10,5-11,5
Част
Накоп част

Пусть X₁ –начало интервала с частотой 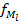, X₂ –конец этого интервала до (X₁,X₂) накопленная частота f

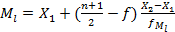n=60

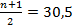
По правилам нахождения медианы для дискретных признаков надо искать полусумму 30 и 31-ого значений в упорядоченном ряду наблюдений

X₁=8,5 X₂=9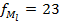,5 f=15

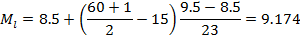
Графически медиану можно определить по кумуляте.

Среднее арифметическое (выборочное среднее).

Среднее арифметическое 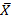и является осн мерой центральной тенденции в мат статистике. Если X_1,X_2,…X_n –ряд наблюдений измеряемого признака в выборке объема n, то среднее арифм или выборочное среднее вычисляется по формуле

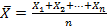или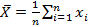

Если признак является дискретным и построен дискретный вариационный ряд

Варианты	v1v2…vk
частоты	m1m2…mk

Где k-общее число вариант, то ф-ла вычисления среднего арифметического упрощается (повторяющееся значения заменяются произведениями) т.е.

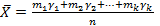или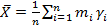

Если для признака построен интервальный вариационный ряд, то среднее ариф вычисляется так же, как и в случае дискретного вариационного ряда, только вместо вариант берутся середины интервалов.

Среднее гармоническое

Обозначается буквой Н. Является довольно специфической мерой, применяется для оценок достаточно редко (напр, когда необх усреднять время выполнения стандартного задания для людей с разной скоростью его выполнения). Формула для вычисления среднего гармонического имеет вид:

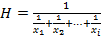или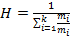

Для интервальных вариационных рядов в качестве вариант берутся середины интервалов.

Среднее геометрическое

Среднее геометрическое G также довольно редко используемая мера центральной тенденции, которая используется для нахождения средних темпов роста какого-то признака на протяжении нескольких одинаковых промежутков времени. Формула для вычисления ср геом имеет вид

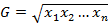
Между рассмотренными средними существует соотношение такое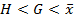

Показатели вариации

Размах вариации. Лимиты.

Размах вариации (РВ) – разность наибольшего и наименьшего признаков выборки. РВ=x_max-x_min Лимиты - x_max и x_min

РВ показывает общую границу изменчивости признака. Этот показатель является слишком поверхностной оценкой, т.к. не дает представления об особенностях распределения значений внутри общих границ.

1, 2, 4, 5, 7, 8, 10, 11 и 1, 5, 5, 6, 6, 7, 7, 11

Например, есть ряды наблюдений, они имеют одни и те же лимиты x_min=1, x_max=11. Для них размах вариации один и тот же, но значения признаков имеет совершенно отчетливое различие в расположении. В первом случае значения равномерно располагаются по всей области. Во втором случае концентрируются около значения 6.

Среднее линейное отклонение.

Среднее линейное отклонение МД – среднее арифметическое абсолютных величин отклонений.

МД = 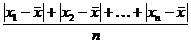или МД=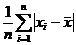

Формула проста, на практике практически не используется, т.к. плохо согласуется с теоретическими оценками теории вероятностей.

Выборочная дисперсия.

Чтобы избежать необходимости оценивать отклонение по абсолютной величине используют выборочную дисперсию ( 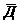). Для вычисления выборочной дисперсии в формуле для среднего отклонения абсолютные величины отклонений заменяют их квадратами, а в знаменателе n заменяют на n-1, т.е.

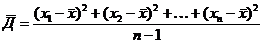или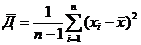

В случае, когда признак является дискретным и для него составлен дискретный вариационный ряд вида

вариата	ν1	ν2	…	νk
частота	m1	m2	…	mk

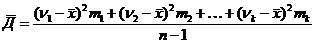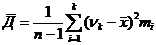Тогда дисперсия вычисляется по формуле или k<n

Если для признака составлены интервальный вариационный ряд, то вместо вариант берутся середины интервалов.

Стандартное отклонение.

Выборочная дисперсия вычисляется как среднее квадратов отклонения. Возведение в квадрат несколько меняет оценку вариации. Чтобы избавится от такого измерения вместо диперсии используют стандартное отклонение, которое вычисляют

Ассиметрия и эксцесс

При оценке свойств измеряемого признака большое значение имеет симметрия частот отклонений относительно среднего арифметического. Она сказывается на форме кривой распределения. Пусть по ряду наблюдения вычислено среднее арифметическое и ряд отклонения. Распределение частот симметрично, если отклонения со знаком «+» встречаются столько раз, сколько такие же отклонения по абсолютной величине со знаком «-». Симметрию легко выявить по полигону или гистограмме. Ветви полигона симметричны относительно вершины. Для количественной оценки несимметричности распределения введен коэффициент ассиметрии (ассиметрия), который вычисляется по формуле:

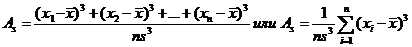-показатель ассиметрии, где s – стандартное отклонение.

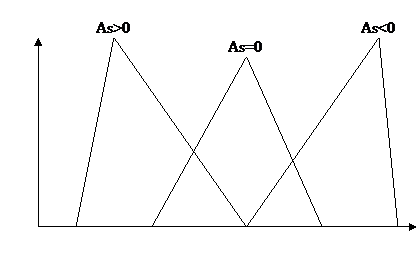
Если А_s=0 распределение частот симметричное.

Если A_s>0, э.зн., что чаще встречаются отклонения со знаком «+» и говорят о правосторонней симметрии.

Если A_s<0, э.зн., что чаще встречаются отклонения со знаком «-» и говорят о левосторонней симметрии.

Эксцесс

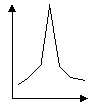(Обозначается Ex) – это показатель, который описывает формулу кривой распределения в смысл островершинности или плосковершинности. Чаще всего этот показатель используют для описания унимодальных распределений частот.

Вершина полигона острая, если небольшое число вариант около моды имеет превосходство в величине частоты.

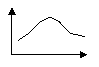Если варианты в районе моды имеют примерно сравнимые частоты, то полигон будет плосковершинным.

Значение эксцесса вычисляется по формуле:

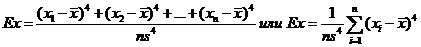
Если Eх=0, то распределение характеризуется как нормальное.

Если Eх>0, распределение островершинное.

Если Eх<0, распределение плосковершинное.
58. Эмпирическая функция распределения

Пусть имеется статистический ряд сгруппированных данных случайной величины Х. Эмпирической функцией распределения или функцией распределения выборки называется функция F*(x) определяемая для любых х относительную частоту событий Х<х => F*(х)= 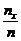, где n_x – число вариант меньше х. По определению эмпирические функции распределения зависят от выборки

1. ее значения принадлежат [0,1];

2. неубывающая;

3. х₁ – наименьшая вариация, х₂ – наибольшая вариация

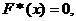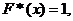x<x₁; x>x₂

Построим эмпирическую функцию распределения по данной таблице сгруппированных данных:

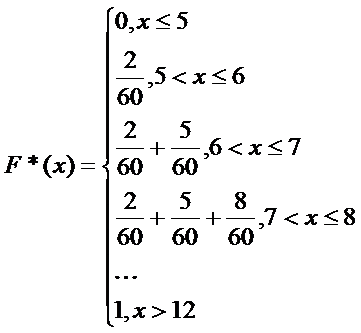
При некоторых расчетах интервальный вариационный ряд заменяют дискретным вариационным рядом. В качестве значений признака берут середины интервалов.