Тема 5: Выравнивание вариационных рядов (построение теоретических распределений).
Наиболее часто используются законы распределения нормальный и Пуассона.
График нормального распределения имеет форму колоколообразной кривой, симметричной относительно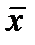 
, концы которой асимптотически приближаются к оси абсцисс. Она имеет точки перегиба, абсциссы которых находятся на расстоянии s от центра симметрии. Эта кривая выражается уравнением:
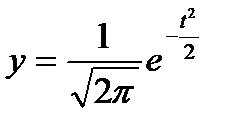
где у – ордината кривой нормального распределения;
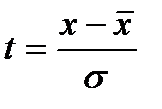- нормированные отклонения.
При выравнивании вариационного ряда по кривой нормального распределения теоретические частоты ряда определяются по формуле
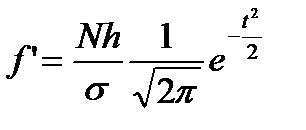
где N= åf – сумма всех частот вариационного ряда;
h – величина интервала в группах (классах);
s - среднее квадратическое отклонение;
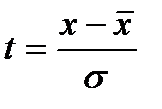- нормированное отклонение вариантов от средней арифметической.
Значение ординат кривой нормального распределения будет соответствовать величине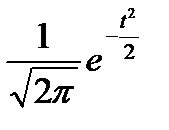 
, которая табулирована и определяется по таблицам значений данной функции j(t) (приложение 1).
Распределение Пуассона.В целом ряде случаев, если вариационный ряд представляет собой распределение по дискретному признаку, где по мере увеличения значений признака х частоты резко уменьшаются и где средняя арифметическая ряда равна или близка по значению к дисперсии, т.е. 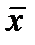=s2, то такой ряд можно выровнять по кривой Пуассона, аналитическое выражение которой
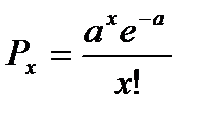
где Рх – вероятность наступления отдельных значений х;
а =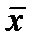 
– средняя арифметическая ряда.
Теоретические частоты при выравнивании эмпирических данных определяются по формуле:
f’ =N Px ,
где f ’- теоретические частоты;
N – общее число единиц ряда.
После выравнивания ряда, т.е. нахождения теоретических частот, возникает необходимость проверить, случайны или существенны расхождения между эмпирическими и теоретическими частотами, и тем самым проверить правильность выдвинутой при выравнивании ряда гипотезы о наличии того или иного характера распределения в эмпирическом ряду.
Для оценки близости эмпирических (f) и теоретических (f ’ ) частот можно применить один из критериев согласия: критерий Пирсона (c2 – «хи-квадрат»), критерий Романовского, критерий Колмогорова (l - «лямбда»).
Критерий Пирсона (c2)представляет собой сумму отношений квадратов расхождений между f и f ‘ к теоретическим частотам:
.
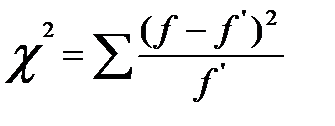Фактическое значение c2 сравнивают с критическим, определяемым по специальным таблицам (приложение 2) в зависимости от принимаемого уровня значимости и числа степеней свободы.
Уровень значимости (a) – вероятность допуска ошибки в утверждении гипотетического закона (характера) распределения – обычно принимается равным 5 % (a=0,05).
Число степеней свободы (k) рассчитывается: k = m – 1 – b
Где m – число групп в ряду распределения; b - число параметров эмпирического распределения, использованных для нахождения теоретических частот. Так, при выравнивании по кривой нормального распределения число степеней свободы k = m – 1 – 2, поскольку при расчете теоретических частот используется два параметра эмпирического распределения (b=2: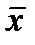 
и s), т.е. k = m –3. для закона Пуассона b = 1 (а = )
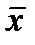Если фактическое c2 оказывается меньше табличного (критического), то расхождения между эмпирическими и теоретическими частотами можно считать случайными.
Критерием Романовского: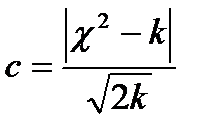 
Если указанное отношение меньше 3, то расхождения считают случайными, если больше 3, то они существенны.
Критерий Колмогорова (l) основан на определении максимального расхождения между накопленными частотами эмпирического и теоретического распределений:
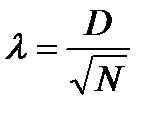
где D – максимальная разность между накопленными частотами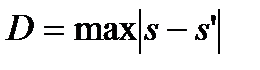 
;
N – сумма всех частот.
Далее по таблицам находится Р(λ) (приложение 3). Чем вероятность ближе к 1, тем увереннее мы можем утверждать, что расхождения между частотами случайны.
На основании полученных значений критериев согласия делаются выводы о близости эмпирических и теоретических частот, таким образом, подтверждается или опровергается гипотеза о наличии того или иного характера распределения в эмпирическом ряду.
Пример1.
Пусть имеется следующее распределение 200 проб нити по крепости (графы 1 и 2 таблицы).
Исходя из гипотезы о нормальном распределении результатов испытаний необходимо выравнять ряд по кривой нормального распределения (т.е. рассчитать теоретические частоты) и оценить близость эмпирических и теоретических частот с помощью критериев согласия: Пирсона (c2), Романовского и Колмогорова (l).
| Крепость нити, г | Число проб | Середина интервала | 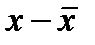 | 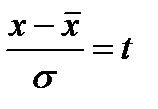 | j(t) | 154*j(t)»f ‘ |
| 120 – 130 | -36,4 | -2,80 | 0,008 | |||
| 130 – 140 | -26,4 | -2,03 | 0,051 | |||
| 140 – 150 | -16,4 | -1,26 | 0,180 | |||
| 150 – 160 | -6,4 | -0,49 | 0,354 | |||
| 160 – 170 | 3,6 | 0,28 | 0,384 | |||
| 170 – 180 | 13,6 | 1,05 | 0,230 | |||
| 180 – 190 | 23,6 | 1,82 | 0,076 | |||
| 190 – 200 | 33,6 | 2,58 | 0,014 | |||
| Итого | - | - | - | - |
Для нахождения теоретических частот используем формулу:
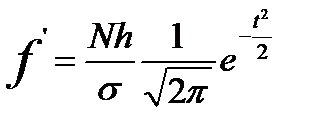, или 
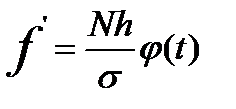
где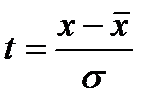 
- нормированные отклонения от средней, т.е. 
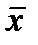и s - основные параметры кривой нормального распределения.
С них и начнем свои расчеты. Опуская вычисления, запишем результаты:
1) 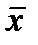= 161,4;
2) s = 13.
Дальнейшие расчеты таковы:
3) находим отклонения отдельных вариантов от средней (графа 4);
4) делим каждое отклонение на s, т.е. находим нормированные отклонения 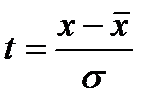(графа 5);
5) зная t, находим по таблицам j(t) (графа 6);
6) рассчитаем постоянный множитель const = Nh/s. В нашем примере const = 200*10/13 = 154;
7) умножая последовательно 154 на j(t)и округляя результаты до целых чисел, находим теоретические частоты (графа 7).
Как видно из таблицы, теоретические частоты (f ‘) , близки к эмпирическим (f), хотя отдельные расхождения имеют место.
Для суждения о случайности или существенности этих расхождений используем ряд критериев согласия:
1. Критерий Пирсона: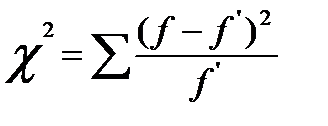 
Расчет этого критерия рассмотрен в таблице:
| f | f ‘ | f – f ‘ | (f – f ‘)2 | (f – f ‘)2/f ‘ |
| -1 | 0,04 | |||
| 0,16 | ||||
| -3 | 0,15 | |||
| -1 | 0,03 | |||
| 0,33 | ||||
| - | - | c2 = 0,71 |
В рассматриваемом примере ряд имеет 8 групп (классов) вариантов, следовательно, и 8 групп частот. Поэтому число степеней свободы для последних (при выравнивании по кривой нормального распределения) k = 8 – 3 = 5. Примем наиболее часто используемый уровень значимости a = 0,05 и обратимся к таблицам («Значения c2 – критерия Пирсона» при различных значениях уровня значимости (0,05; 0,01 и т.д.)).
По таблицам значений c2- критерия Пирсона для степеней свободы k = 5 и уровня значимости a = 0,05 определяем, что c2табл.= 11,07. Так как полученное в задаче фактическое значение c2факт.= 0,71, т.е. меньше табличного, то, следовательно, можно считать случайными расхождения между эмпирическими и теоретическими частотами и выдвинутая гипотеза о близости эмпирического распределения к нормальному не опровергается.
2. Применим критерий Романовского:
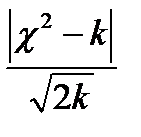
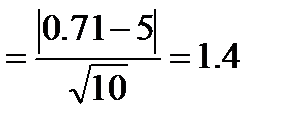
Поскольку 1,4< 3, то можно считать расхождения между эмпирическими и теоретическими частотами случайными.
3. Попробуем проверить нашу гипотезу с помощью критерия Колмогорова ( 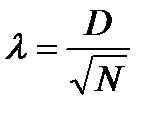). Для этого запишем накопленные частоты эмпирического и теоретического распределений и найдем максимальный разрыв между ними:
| f | f ’ | Накопленные частоты | ês – s’ ê | |
| эмпирическое (s) | теоретическое (s’) | |||
Максимальный разрыв D = 2, поэтому =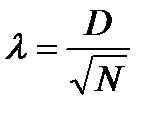 
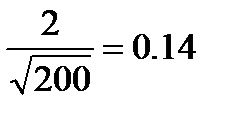
По таблицам значений функции P(l) находим для l = 0,2, что Р = 1,000. Следовательно, вполне можно полагать, что расхождения между f и f ‘ носят случайный характер.
Пример 2.
В течение рабочей недели производилось наблюдение за работой 50 станков и регистрировались неисправности, требовавшие остановки станков для их регулировки. Результаты наблюдений следующие:
| Число неисправностей (х) | ||||||
| Число станков (f) |
Требуется:
1) вычислить вероятности и теоретические частоты числа неисправностей, считая, что распределение последних подчиняется закону Пуассона;
1) оценить близость эмпирических и теоретических частот с помощью критериев Пирсона, Романовского и Колмогорова.
Решение:
а) Рассчитаем среднее число неисправностей:
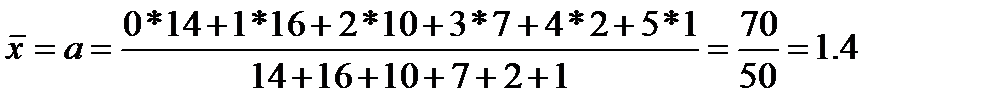
б) Находим по таблицам значение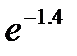 
=0,2466.
в) Подставляя в формулу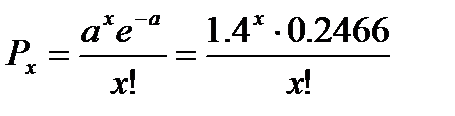 
значения 
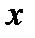= 0,1,2,3,4,5 получаем вероятности числа неисправностей от 0 до 5.
г) Умножив последние на 50 (общее число единиц распределения), получим теоретические частоты числа неисправностей, т.е.
.
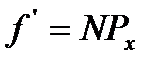Значения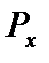 
и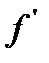 
(округленные до целого числа) показаны в приводимой ниже таблице:
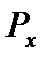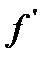 |  (теоретические частоты)= 50 |
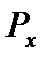| 0,2466 | |
| 0,3452 | |
| 0,2417 | |
| 0,1128 | |
| 0,0395 | |
| 0,0111 | |
| Итого |
Для оценки близости эмпирических и теоретических частот воспользуемся критериями Пирсона, Романовского и Колмогорова.
1) Критерий Пирсона: .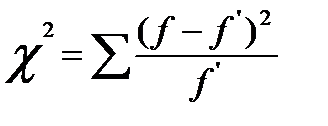
Все расчеты показаны в таблице:
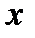 | f | f ‘ | f - f ‘ | (f - f ‘ )2 | (f - f ‘ )2/f ‘ |
| 0.33 | |||||
| -1 | 0.06 | ||||
| -2 | 0.33 | ||||
| 0.17 | |||||
Фактическое значение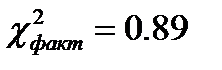 
.
Находим критическое (табличное) значение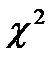 
при k = 6 – 2 =4 и 
, 
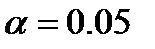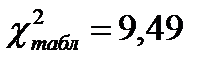. Так как 
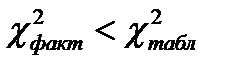, т.е. 0.89< 9.49, то имеем все основания считать расхождения между эмпирическими и теоретическими частотами случайными, а следовательно, не опровергнутой гипотезу о том, что распределение числа неисправностей подчиняется закону Пуассона.
2) Применим критерий Романовского: =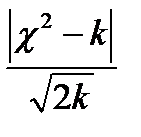 
.
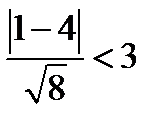Следовательно, расхождения случайны.
3) По критерию Колмогорова получаем: .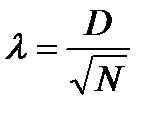
| Накопленные частоты |  | |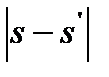
| Эмпирические (s) | Теоретические (s‘ ) | |
| 2 (D) | ||
Таким образом,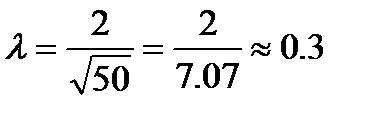 
.
По таблицам находим, что P(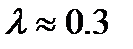 
) »1.
Итак, все три критерия оценивают расхождения между эмпирическими и теоретическими частотами как случайные, не опровергая тем самым выдвинутую гипотезу о том, что распределение станков по числу неисправностей подчиняется закону Пуассона.
Задание 8.
В течение рабочей недели производилось наблюдение за работой 65 станков и регистрировались неисправности, требовавшие остановки станков для их регулировки. Результаты наблюдений следующие:
| Число неисправностей (х) | 0 | 1 | 2 | 3 | 4 | 5 |
| Число станков (f) | 17 | 19 | 13 | 10 | 5 | 1 |
Требуется: 1) вычислить вероятности и теоретические частоты числа неисправностей, считая, что распределение последних подчиняется закону Пуассона; 2) оценить близость эмпирических и теоретических частот с помощью критериев Пирсона, Романовского и Колмогорова.
Решение:
1) Так как вариационный ряд представляет собой распределение по дискретному признаку, где по мере увеличения значений признака х частоты резко уменьшаются, то выдвигаем гипотезу о близости данного распределения к распределению Пуассона и производим выравнивание ряда распределения в соответствии с этой гипотезой. Теоретические частоты при выравнивании эмпирических данных определяем по формуле: f’=N*Px,
где f ’- теоретические частоты;
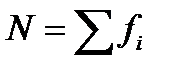– общее число единиц ряда, в нашем примере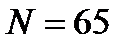 
Рх – вероятность наступления отдельных значений х, которая определяется по формуле: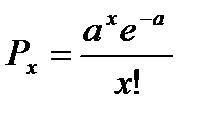 
,
где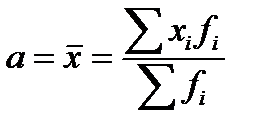 
– средняя арифметическая ряда. Следовательно, взяв данные из нижестоящей таблицы получим: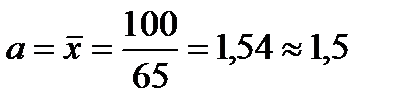 
Представим расчет теоретических частот в табличном виде:
| Число неисправностей (хi) | Число станков ( 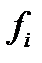 ) | 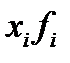 | 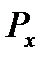 | f’=65*Px |
| 0 | 17 | 0 | 0,224 | 15 |
| 1 | 19 | 19 | 0,336 | 22 |
| 2 | 13 | 26 | 0,252 | 16 |
| 3 | 10 | 30 | 0,126 | 8 |
| 4 | 5 | 20 | 0,047 | 3 |
| 5 | 1 | 5 | 0,014 | 1 |
| Итого | 65 | 100 | - | 65 |
Покажем пример промежуточного расчета:
для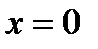 
получаем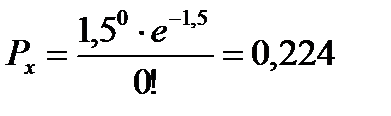 
для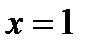 
получаем 
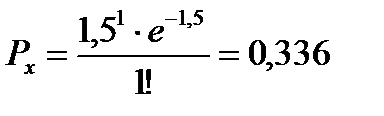и т.п.
Затем находим теоретические частоты ряда распределения:
Для х=0 получаем f’=65* 0,224=14,56≈15,
Для х=1 получаем f’=65* 0,336=21,84≈22 и т.д. (расчет представлен в таблице).
После выравнивания ряда, т.е. нахождения теоретических частот, необходимо проверить, случайны или существенны расхождения между эмпирическими и теоретическими частотами, и тем самым проверить правильность выдвинутой при выравнивании ряда гипотезы о близости исходного распределения к распределению Пуассона.
2) Для оценки близости эмпирических (f) и теоретических (f ’ ) частот применяем критерии согласия: критерий Пирсона (c2 – «хи-квадрат»), критерий Романовского, критерий Колмогорова (l - «лямбда»).Расчет промежуточных значений приведен в таблице ниже:
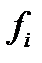| | f’ | 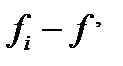 | 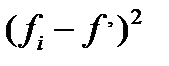 |  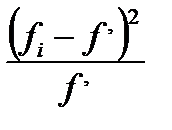| s (накопленные частоты ряда 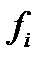 ) | s (накопленные частоты ряда f ’) |  |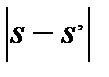
| 17 | 15 | -2 | 4 | 0,267 | 17 | 15 | 2 |
| 19 | 22 | -3 | 9 | 0,409 | 36 | 37 | 1 |
| 13 | 16 | -3 | 9 | 0,563 | 49 | 53 | 4 =D |
| 10 | 8 | 2 | 4 | 0,500 | 59 | 61 | 2 |
| 5 | 3 | 2 | 4 | 1,333 | 64 | 64 | 0 |
| 1 | 1 | 0 | 0 | 0 | 65 | 65 | 0 |
| ∑ = 65 | ∑ =65 | - | - |  | - | - | - |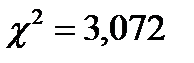
Критерий Пирсона (c2) представляет собой сумму отношений квадратов расхождений между f и f ‘ к теоретическим частотам:
.
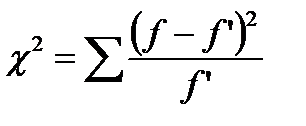Фактическое значение c2 = 3,072 сравниваем с критическим, определяемым по специальным таблицам (приложение 2) в зависимости от принимаемого уровня значимости и числа степеней свободы.
Уровень значимости (a) – вероятность допуска ошибки в утверждении гипотетического закона (характера) распределения – обычно принимается равным 5 % (a=0,05 ).
Число степеней свободы (k) рассчитывается: k = m – 1 – b ,
Где m – число групп в ряду распределения; b - число параметров эмпирического распределения, использованных для нахождения теоретических частот, для закона Пуассона b = 1 (а= 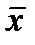), следовательно k =6-1-1=4. Таким образом определяем критическое табличное значение 
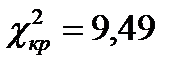(см. приложение 2 для 
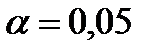и k = 4).
Так как фактическое c2=3,072 оказывается меньше табличного (критического) 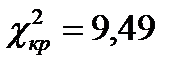, то расхождения между эмпирическими и теоретическими частотами можно считать случайными, т.е. гипотезу о близости фактического распределения к распределению Пуассона принимаем.
Критерий Романовского: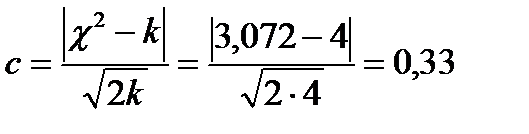 
Так как с < 3, то расхождения между фактическими и теоретическими частотами считаем случайными, гипотезу о распределении Пуассона принимаем.
Критерий Колмогорова (l) основан на определении максимального расхождения между накопленными частотами эмпирического и теоретического распределений: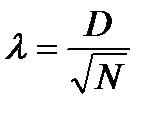 
где D – максимальная разность между накопленными частотами ;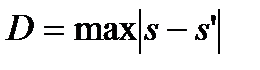
N – сумма всех частот ряда распределения.
Расчет величины D представлен в таблице (см. выше).Следовательно найдем значение критерия: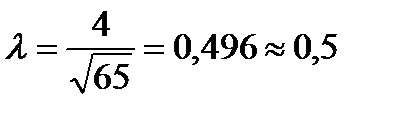 
Далее находится вероятность Р(λ) (приложение 3). Чем ближе вероятность к 1, тем с большей уверенностью можно утверждать, что расхождения между эмпирическими и теоретическими частотами случайны, и, таким образом, подтвердить или опровергнуть гипотезу о наличии того или иного характера распределения в эмпирическом ряду.
В нашем случае Р(λ)=0,9639, т.е. с вероятностью 96,39% можно утверждать, что расхождения между фактическими и теоретическими частотами случайны, следовательно гипотезу можно принять с этой вероятностью.
Задание 9.
Пусть имеется следующее распределение на основании данных о содержании меди (в %) в 500 образцах сплава.
Исходя из гипотезы о нормальном распределении результатов испытаний необходимо выравнять ряд по кривой нормального распределения (т.е. рассчитать теоретические частоты) и оценить близость эмпирических и теоретических частот с помощью критериев согласия: Пирсона (c2), Романовского и Колмогорова (l).
| Содержание меди, % х | Количество образцов, f |
| 56 – 58 | 5 |
| 58 – 60 | 29 |
| 60 – 62 | 63 |
| 62 – 64 | 116 |
| 64 – 66 | 117 |
| 66 – 68 | 102 |
| 68 – 70 | 48 |
| 70 – 72 | 14 |
| 72 – 74 | 6 |
| Итого | 500 |
Решение:
1) Выдвигаем гипотезу о близости представленного распределения к нормальному. При выравнивании вариационного ряда по кривой нормального распределения теоретические частоты ряда определяем по формуле
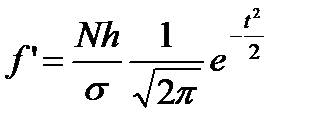
где N= åf – сумма всех частот вариационного ряда;
h – величина интервала в группах;
s - среднее квадратическое отклонение;
t - нормированное отклонение вариантов от средней арифметической, которое определяется по формуле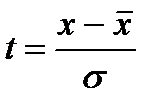 
.
Значение ординат кривой нормального распределения будет соответствовать величине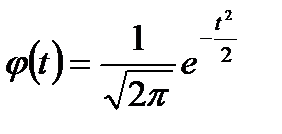 
, которая табулирована и определяется по таблицам значений данной функции j (t) (приложение 1).
Расчет показателей представлен в таблице:
| Содержание меди, % х | Количество образцов, f | Середина интервала,хi | 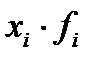 | 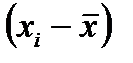 | 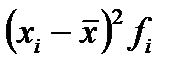 | t | j (t) |  |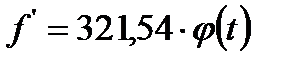
| 56 – 58 | 5 | 57 | 285 | -7,7 | 296,45 | 2,48 | 0,0184 | 6 |
| 58 – 60 | 29 | 59 | 1711 | -5,7 | 942,21 | 1,83 | 0,0748 | 24 |
| 60 – 62 | 63 | 61 | 3843 | -3,7 | 862,47 | 1,19 | 0,1965 | 63 |
| 62 – 64 | 116 | 63 | 7308 | -1,7 | 335,24 | 0,55 | 0,3429 | 110 |
| 64 – 66 | 117 | 65 | 7605 | 0,3 | 10,53 | 0,10 | 0,3970 | 128 |
| 66 – 68 | 102 | 67 | 6834 | 2,3 | 539,58 | 0,74 | 0,3034 | 98 |
| 68 – 70 | 48 | 69 | 3312 | 4,3 | 887,52 | 1,38 | 0,1539 | 50 |
| 70 – 72 | 14 | 71 | 994 | 6,3 | 555, 66 | 2,03 | 0,0508 | 16 |
| 72 – 74 | 6 | 73 | 438 | 8,3 | 413,34 | 2,67 | 0,0113 | 4 |
| Итого | 500 | - | 32330 | - | 4843,00 | - | - | 499 |
Исходя из данных таблицы получаем:
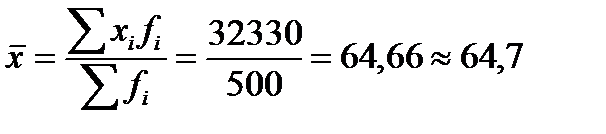- средняя арифметическая.
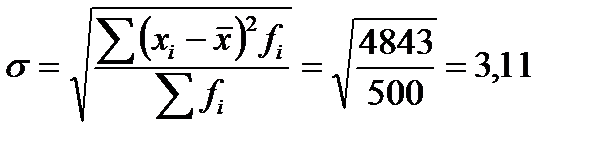- среднее квадратическое отклонение.
Теперь можно рассчитать значения t для каждой группы ряда распределения: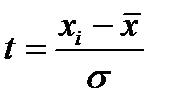 
(см. расчетную таблицу).
На следующем этапе решения определим значение функции j (t) по специальным таблицам (см. приложение 1:номер строки в таблице соответствует целым и десятым значения t, номер столбца соответствует сотой доле в значении t).
Теперь можно рассчитать теоретические частоты ряда в соответствии с гипотезой о нормальном распределении: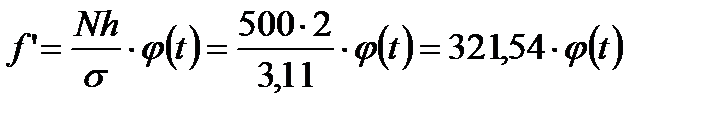 
(смотри соответствующий столбик значений в таблице).
После выравнивания ряда, т.е. нахождения теоретических частот, необходимо проверить, случайны или существенны расхождения между эмпирическими и теоретическими частотами, и тем самым проверить правильность выдвинутой при выравнивании ряда гипотезы о близости исходного распределения к нормальному распределению.
2) Для оценки близости эмпирических (f) и теоретических (f ’ ) частот применяем критерии согласия: критерий Пирсона (c2 – «хи-квадрат»), критерий Романовского, критерий Колмогорова (l - «лямбда»).Расчет промежуточных значений, абсолютно аналогичен заданию 8 и приведен в нижеследующей таблице:
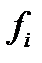| | f’ | 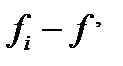| 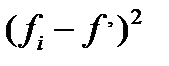| 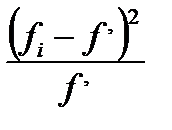| s (накопленные частоты ряда 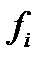) | s (накопленные частоты ряда f ’) | |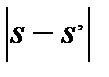
| 5 | 6 | -1 | 1 | 0,167 | 5 | 6 | 1 |
| 29 | 24 | 5 | 25 | 1,042 | 34 | 30 | 4 |
| 63 | 63 | 0 | 0 | 0,000 | 97 | 93 | 4 |
| 116 | 110 | 6 | 36 | 0,327 | 213 | 203 | 10=D |
| 117 | 128 | -11 | 121 | 0,945 | 330 | 331 | 1 |
| 102 | 98 | 4 | 16 | 0,163 | 432 | 429 | 3 |
| 48 | 50 | -2 | 4 | 0,080 | 480 | 479 | 1 |
| 14 | 16 | -2 | 4 | 0,250 | 494 | 495 | 1 |
| 6 | 4 | 2 | 4 | 1,000 | 500 | 499 | 1 |
| 500 | 499 | - | - | 3,974 | - | - | - |
Рассчитаем критерии согласия:
- критерий Пирсона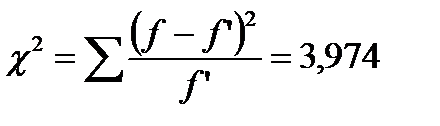 
, найдем критическое значение 
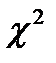(см. приложение 2) на основани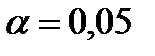и 
и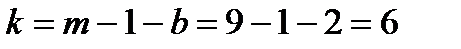 
,
где m – число групп в ряду распределения;
b - число параметров эмпирического распределения, использованных для нахождения теоретических частот (при выравнивании по кривой нормального распределения число степеней свободы k = m-1-2, поскольку при расчете теоретических частот используется два параметра эмпирического распределения (b=2: 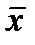и s)). Следовательно, 
.
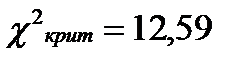Так как фактическое c2=3,974 оказывается меньше табличного (критического)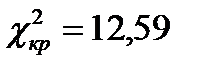 
, то расхождения между эмпирическими и теоретическими частотами можно считать случайными, т.е. гипотезу о близости фактического распределения к распределению Пуассона принимаем.
Критерий Романовского: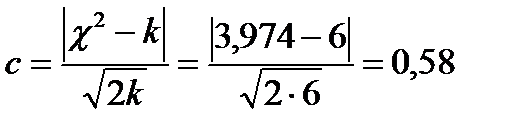 
Так как с < 3, то расхождения между фактическими и теоретическими частотами считаем случайными, гипотезу о распределении Пуассона принимаем.
Критерий Колмогорова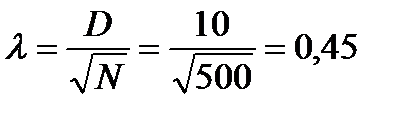 
Теперь определим Р (λ=0,45)=0,9874 (см. приложение 3).Т.е. с вероятностью 98,74% можно утверждать, что расхождения между фактическими и теоретическими частотами случайны, следовательно гипотезу можно принять с этой вероятностью.
Задача 77.
В течение рабочей недели производилось наблюдение за работой 65 станков и регистрировались неисправности, требовавшие остановки станков для их регулировки. Результаты наблюдений следующие:
| Число неисправностей (х) | ||||||
| Число станков (f) |
Требуется: 1) вычислить вероятности и теоретические частоты числа неисправностей, считая, что распределение последних подчиняется закону Пуассона; 2) оценить близость эмпирических и теоретических частот с помощью критериев Пирсона, Романовского и Колмогорова.
Задача 78.
Распределение количества землетрясений (подземных толчков) за месяц на территории региона характеризовалось данными, приведенными в таблице:
| Количество подземных толчков за месяц | Количество районов |
А) Рассчитать теоретические частоты, исходя из гипотезы о распределении Пуассона.
Б) проверить, случайны или нет расхождения между эмпирическими и теоретическими частотами, используя все критерии согласия.
Задача 79.
Пусть имеется следующее распределение на основании данных о содержании меди (в %) в 500 образцах сплава).
Исходя из гипотезы о нормальном распределении результатов испытаний необходимо выравнять ряд по кривой нормального распределения (т.е. рассчитать теоретические частоты) и оценить близость эмпирических и теоретических частот с помощью критериев согласия: Пирсона (c2), Романовского и Колмогорова (l).
| Содержание меди, % х | Количество образцов, f | Середина интервала, хсер | ||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 56 - 58 | ||||||
| 58 - 60 | ||||||
| 60 - 62 | ||||||
| 62 - 64 | ||||||
| 64 - 66 | ||||||
| 66 - 68 | ||||||
| 68 - 70 | ||||||
| 70 - 72 | ||||||
| 72 – 74 | ||||||
| Итого | - |
Задача 80.
Предположим, имеется следующее распределение 40 выборочно обследованных автомобильных шин по пробегу:
| Пробег шин, тыс.км | Число шин |
| 50 – 52 | |
| 52 – 54 | |
| 54 – 56 | |
| 56 – 58 | |
| 58 – 60 | |
| 60 – 62 | |
| Итого |
А) исходя из гипотезы о нормальном распределении, рассчитать теоретические частоты в данном ряду.
Б) с помощью критериев согласия проверить, согласуется ли эмпирическое распределение с гипотетическим нормальным.
Задача 81.Распределение 1000 семей по уровню душевого дохода за месяц характеризуется данными:
| Группы семей по среднедушевому доходу в месяц, руб. | Число семей | Частоты теоретического нормального распределения |
| До 500 | ||
| 500-600 | ||
| 600-700 | ||
| 700-800 | ||
| 800-900 | ||
| 900-1000 | ||
| 1000-1100 | ||
| 1100-1200 | ||
| 1200-1300 | ||
| 1300 и более | ||
| Итого |
На основе критериев согласия Пирсона, Романовского и Колмогорова проверьте, согласуется ли распределение семей по среднедушевому доходу с нормальным.