Понятие ранга матрицы и его свойства

Определение. Рангом матрицы А называется наивысший порядок отличного от нуля определителя, который можно построить из элементов данной матрицы.

Обозначение ранга матрицы А:

rang(A) = r (где r – число).

Можно дать другое определение ранга, сформулированное с помощью понятия минора. Для этого введем понятие минора матрицы.

Если в матрице А_mxn выбрать произвольно s строк и s столбцов
(0 £ s £ min (m,n)), то определитель матрицы, полученный на пересечении выбранных строк и столбцов, называется минором порядка s данной матрицы. Тогда ранг матрицы определяют как наибольший из порядков её миноров (r), отличных от нуля, а любой минор порядка r, отличный от нуля, называется базисным минором.

Приведем простые примеры вычисления ранга матрицы:

1)rang 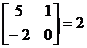, 2) rang 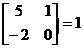3) rang .

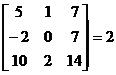Свойства ранга матрицы

1. Для матрицы А_mxn ранг матрицы может меняться в пределах:

0 £ rang £ min (m,n).

2. rang = 0 тогда и только тогда, когда все элементы матрицы равны нулю.

3. Для квадратной матрицы А_n ранг равен n (rang(A) = n) тогда и только тогда, когда матрица А_n – невырожденная.

4. Ранг матрицы не меняется при транспонировании матрицы.

5. Ранг матрицы не меняется при элементарных преобразованиях матрицы.

Элементарными преобразованиями матрицы являются:

1. Перестановка местами любых двух строк (столбцов) матрицы.

2. Умножение каждого из элементов какой-либо строки (столбца) на число, отличное от нуля.

3. Прибавление к каждому элементу какой-либо строки (столбца), соответствующих элементов другой строки (столбца), умноженных на одно и то же число.

Вычисление ранга матрицы

Перечислим основные способы вычисления ранга матрицы:

1. Простой перебор определителей.

2. Метод окаймляющих миноров.

3. Метод элементарных преобразований – приведение с помощью элементарных преобразований матрицы А к трапециевидной матрице А¢ того же ранга.

Простой перебор определителей

Рассмотрим использование данного способа на конкретном примере.

Пример 2.Вычислить ранг матрицы .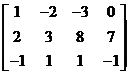

Решение.

Вычислим все определители третьего порядка, которые могут быть построены из элементов данной матрицы.

, , , .

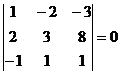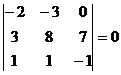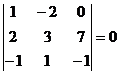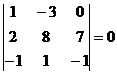Все определители 3-го порядка оказались равны нулю (подматрицы третьего порядка вырождены). Перейдем к вычислению определителей второго порядка.

.

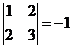Так как определитель 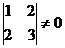(подматрица второго порядка не вырождена), то ранг матрицы по определению равен двум:

.

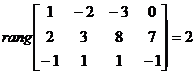Ответ: r = 2.

Метод окаймляющих миноров

Пусть в матрице найден минор к-го порядка М, отличный от нуля. Рассмотрим лишь те миноры (к+1)-го порядка, которые содержат в себе (окаймляют) минор М: если все они равны нулю, то ранг матрицы равен к. В противном случае среди окаймляющих миноров найдется ненулевой минор (к+1)-го порядка, и вся процедура повторяется.

Пример 3.Найти ранг матрицы .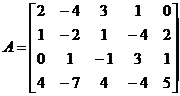

Решение.

Фиксируем минор 2-го порядка, отличный от нуля:

.

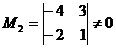Минор 3-го порядка, окаймляющий минор М₂, также отличен от нуля:

.

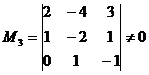Однако, оба минора 4-го порядка, окаймляющие М₃, равны нулю:

М₄ = 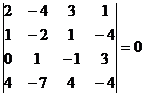, М₄ = .

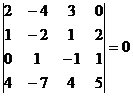Поэтому ранг матрицы равен трем (r = 3).

Ответ: r = 3

Метод элементарных преобразований

Метод элементарных преобразованийоснован на том факте, что элементарные преобразования не меняют её ранга. Используя эти преобразования, любую матрицу можно привести к трапециевидному виду, или к такому виду, когда все её элементы, кроме главных диагональных элементов 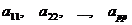, равны нулю.

Удобно, когда главные диагональные элементы трапециевидной матрицы равны единице, т.е. трапециевидная матрица имеет вид:

.

Тогда ранг матрицы равен числу главных диагональных элементов (в данном случае – единиц), отличных от нуля.

Пример 4. Найти ранг матрицы .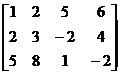

Решение.

Приведем исходную матрицу к трапециевидной форме.

® ® ® ® .

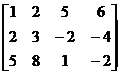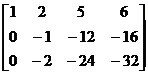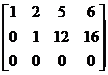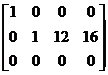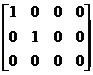Число единиц, стоящих на главной диагонали полученной трапециевидной матрицы равно двум, следовательно, ранг этой матрицы равен двум, таков же и ранг исходной матрицы, т.е. r = 2.

Ответ: r = 2.

Литература по теме:

а) основная

1. Кремер Н.Ш. Высшая математика для экономического бакалавриата: учебник и практикум. М.: Юрайт, 2014. – 909 с. (ЭБС ЮРАЙТ. – https://www.biblio-online.ru/viewer/EDF405ED-E895-42DE-9744-ED48C83187DC#/).

б) дополнительная

2. Красс М.С. Математика в экономике. Базовый курс. М.: Юрайт, 2015. – 471 с. (ЭБС ЮРАЙТ. – https://www.biblio-online.ru/viewer/8BD2AC05-D7E3-4B22-844C-3DC3D6F52A1B#/).