С постоянными коэффициентами
Неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами имеет вид 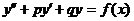 .
.
Общее решение данного уравнения находится по формуле 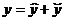 , где
, где 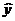 − общее решение соответствующего однородного уравнения
− общее решение соответствующего однородного уравнения 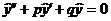 , а
, а 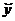 − частное решение неоднородного уравнения
− частное решение неоднородного уравнения 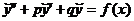 .
.
В простейших случаях, когда функция 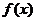 , входящая в исходное уравнение является многочленом, либо показательной функцией, либо тригонометрической функцией
, входящая в исходное уравнение является многочленом, либо показательной функцией, либо тригонометрической функцией 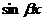 или
или 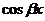 , либо линейной комбинацией перечисленных функций, то частное решение может быть найдено методом неопределенных коэффициентов, не содержащим процесса интегрирования.
, либо линейной комбинацией перечисленных функций, то частное решение может быть найдено методом неопределенных коэффициентов, не содержащим процесса интегрирования.
В дальнейшем будем употреблять символы 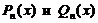 для обозначения многочленов степени
для обозначения многочленов степени 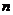 :
: 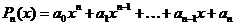 ,
, 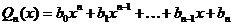 .
.
Рассмотрим некоторые виды правых частей неоднородного исходного уравнения, допускающие применение этого метода.
Правая часть имеет вид 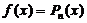
Частное решение 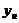 уравнения
уравнения 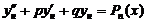 надо искать в виде
надо искать в виде

Во всех случаях 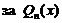 надо взять многочлен с неопределенными коэффициентами, которые находятся после подстановки
надо взять многочлен с неопределенными коэффициентами, которые находятся после подстановки 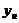 в уравнение.
в уравнение.
Правая часть имеет вид 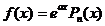
Частное решение 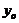 уравнения
уравнения 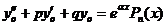 надо искать в виде
надо искать в виде

Во всех случаях 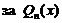 надо взять многочлен с неизвестными коэффициентами, которые определятся после подстановки
надо взять многочлен с неизвестными коэффициентами, которые определятся после подстановки 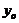 в уравнение.
в уравнение.
Правая часть имеет вид 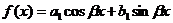
Частное решение 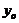 уравнения
уравнения 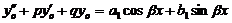 надо искать в виде
надо искать в виде
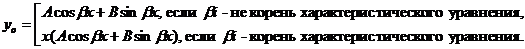
Коэффициенты A и B определяются после подстановки 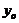 в уравнение.
в уравнение.
Правая часть имеет вид 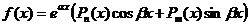 ,
,
где 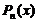 − многочлен степениn, а
− многочлен степениn, а 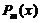 − многочлен степениm.
− многочлен степениm.
Частное решение 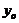 уравнения
уравнения 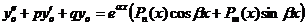 надо искать в виде
надо искать в виде
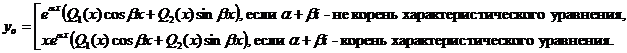
Зависимость частного решения от корней характеристического уравнения 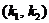 отражена в следующей таблице
отражена в следующей таблице
| Тип | Правая часть диф. уравнения 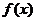 | Корни характеристического уравнения | Виды частного решения 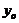 |
| I | 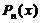 | 1. 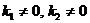 2. 2. 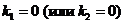  3. 3. 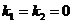 | 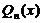 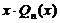 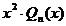 |
| II | 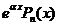 | 1. 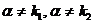 2. 2. 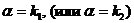 3. 3. 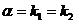 | 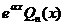 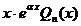 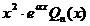 |
| III | 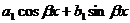 | 1. 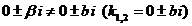 2. 2. 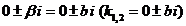 | 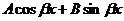 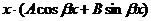 |
| IV | 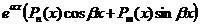 | 1.  2. 2. 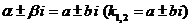 | 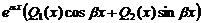 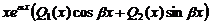 |
Здесь 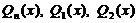 − многочлены, степень которых равна наивысшей степени многочленов
− многочлены, степень которых равна наивысшей степени многочленов 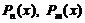 , а коэффициенты многочленов подлежат
, а коэффициенты многочленов подлежат 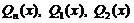 определению.
определению.
Для определения общего вида многочленов 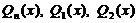 можно воспользоваться следующей таблицей
можно воспользоваться следующей таблицей
Данный многочлен в правой части уравнения 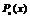 | Наивысшая степень данного многочлена 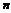 | Общий вид искомого многочлена 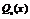 |
2; −37; 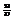 | 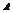 | |
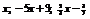 | 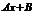 | |
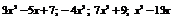 | 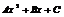 | |
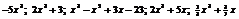 | 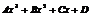 |
Неопределенные коэффициенты многочленов равенства находятся так.
1. В заданное уравнение подставляется частное решение 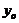 .
.
2. Сравниваются коэффициенты при одинаковых степенях независимой переменной в левой и правой частях.
Ниже на примерах укажем, как это выполняется практически.
Вопросы для самопроверки
1. Дайте определение дифференциального уравнения 1-го порядка.
2. Дайте определение общего решения дифференциального уравнения 1-го порядка.
3. Дайте определение частного решения дифференциального уравнения 1-го порядка.
4. Сформулируйте задачу Коши для дифференциального уравнения 1-го порядка.
5. Укажите геометрический смысл задачи Коши для дифференциального уравнения 1-го порядка.
6. Дайте геометрическое истолкование дифференциального уравнения 1-го порядка, выясните геометрический смысл общего и частного решения.
7. Сформулируйте теорему о существовании и единственности решения дифференциального уравнения 1-го порядка.
8. Найдите общее решение уравнения 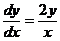 и укажите, где условия теоремы не выполняются.
и укажите, где условия теоремы не выполняются.
9. Дайте определение дифференциального уравнения с разделяющимися переменными.
10. Изложите метод нахождения общего решения дифференциального уравнения с разделяющимися переменными.
11. Дайте определение однородного дифференциального уравнения 1-го порядка.
12. Изложите метод нахождения общего решения однородного дифференциального уравнения 1-го порядка.
13. Дайте определение линейного дифференциального уравнения 1-го порядка.
14. Изложите метод нахождения общего решения линейного дифференциального уравнения 1-го порядка.
15. Дайте определение уравнения Бернулли.
16. Изложите метод нахождения общего решения уравнения Бернулли.
17. Дайте определение дифференциального уравнения в полных дифференциалах.
18. Изложите метод нахождения общего решения дифференциального уравнения в полных дифференциалах.
19. Что называется особым решением дифференциального уравнения?
20. Сформулируйте теорему о существовании и единственности решения дифференциального уравнения 2-го порядка.
21. Какие виды уравнений 2-го порядка допускают понижение порядка?
22. Как понизить порядок уравнения 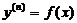 ?
?
23. Что называется частным решением уравнения 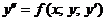 . Сколько начальных условий нужно для того, чтобы найти это частное решение?
. Сколько начальных условий нужно для того, чтобы найти это частное решение?
24. Как понизить порядок уравнения 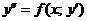 ?
?
25. Как понизить порядок уравнения 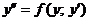 ?
?
26. Какие правила обращения с произвольной постоянной величиной вы усвоили?
27. Как решить задачу Коши для уравнений 2-го порядка?
28. Дайте определение линейного дифференциального уравнения n-го порядка (однородного и неоднородного).
29. Докажите основные свойства частных решений однородного линейного дифференциального уравнения.
30. Дайте определение линейно зависимых и линейно независимых функций.
31. Докажите, что для линейно зависимых функций определитель Вронского равен нулю.
32. Докажите теорему об общем решении однородного линейного дифференциального уравнения 2-го порядка.
33. Изложите метод нахождения общего решения однородного линейного дифференциального уравнения 2-го порядка, если известно одно его частное решение.
34. Выведите формулу для общего решения однородного линейного дифференциального уравнения 2-го порядка с постоянными коэффициентами в случае вещественных различных корней характеристического уравнения.
35. Выведите формулу для общего решения однородного линейного дифференциального уравнения 2-го порядка с постоянными коэффициентами в случае равных корней характеристического уравнения.
36. Выведите формулу для общего решения однородного линейного дифференциального уравнения 2-го порядка с постоянными коэффициентами в случае комплексных корней характеристического уравнения.
37. Докажите теорему об общем решении однородного линейного дифференциального уравнения 2-го порядка.
38. Изложите правило нахождения частного решения линейного дифференциального уравнения 2-го порядка с постоянными коэффициентами и правой частью вида 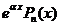 , где
, где 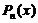 − многочлен степени
− многочлен степени 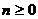 .
.
39. Изложите правило нахождения частного решения линейного дифференциального уравнения 2-го порядка с постоянными коэффициентами и правой частью вида
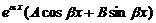 .
.
40. Докажите, что сумма частных решений уравнений
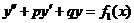 и
и 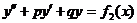
является решением уравнения 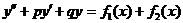 .
.
41. Что называется нормальной системой дифференциальных уравнений 1-го порядка? Сформулируйте задачу Коши для этой системы.
42. Изложите метод для нахождения общего решения нормальной системы дифференциальных уравнений 1-го порядка сведением системы к одному дифференциальному уравнению (метод исключения).
43. Изложите метод для нахождения общего решения нормальной системы двух однородных линейных дифференциальных уравнений с постоянными коэффициентами в случае простых корней характеристического уравнения.
44. Запишите в матричной форме нормальную систему и решение нормальной системы двух однородных линейных дифференциальных уравнений с постоянными коэффициентами
Примеры решения задач
