С постоянными коэффициентами

Методы решения дифференциальных уравнений высшего порядка.

Уравнение вида .

Простейшим уравнением n-го порядка является уравнение вида 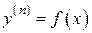. Запишем это уравнение в виде: 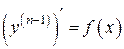. Интегрируя по 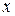левую и правую части выражения, получим 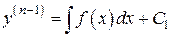. Интегрируя еще раз получим

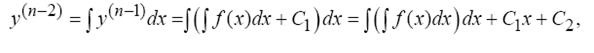
И так далее пока не будет найдено выражение общего интеграла y(x);

Некоторые типы дифференциальных уравнений второго порядка, приводимых к уравнениям первого порядка.

а). Уравнение вида 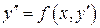(3)

не содержит явным образом искомой функции 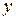. Тогда полагая 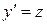, получим 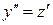. Подставляя эти выражения производных в уравнение (3)

получим 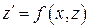– дифференциальное уравнение 1-го порядка относительно неизвестной функции 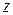от 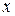. Проинтегрировав это уранение находим его общее решение 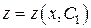, а затем из соотношения 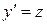получаем общий интеграл уравнения (3):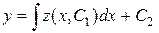

б). Уравнение вида 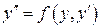не содержит явным образом независимого переменного 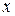. Положим 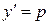, считая 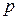– функцией от 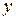, тогда 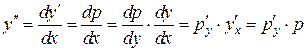. Уравнение приобретет вид 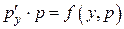, т.е. вид дифференциального уравнения 1-го порядка относительно 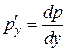. Вычислив 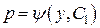будем иметь: 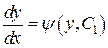или 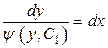. Итак, 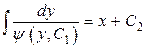– общий интеграл исходного уравнения.

Пример 1. Найти общее решение дифференциального уравнения .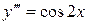

Это уравнение допускает понижение порядка. Перепишем его в виде: 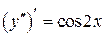или 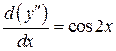, т.е. 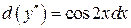. Интегрируя обе части последнего уравнения, получим 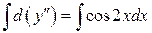или .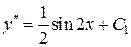

Далее применяем этот же метод еще раз: .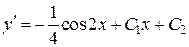

Затем аналогично получим ,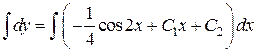

откуда .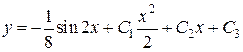

Общее решение примет вид: .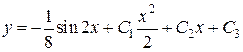

Пример 2. Найти общее решение дифференциального уравнения .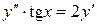

В этом уравнении явно не содержится переменная 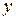, поэтому замена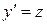 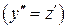обеспечивает понижение порядка дифференциального уравнения. Получим 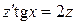или 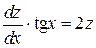, т.е. уравнение с разделяющимися переменными 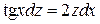. Разделим обе части на 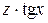и получим 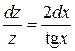. Интегрируем 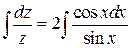или .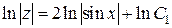

При интегрировании произвольную постоянную обозначим в виде 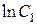для того, чтобы потенцированием упростить выражение:

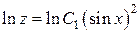или .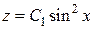

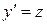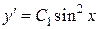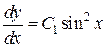Возвращаясь к обозначению , продолжим решение дифференциального уравнения: или , следовательно, 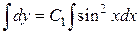. Вычисляя интеграл в правой части понижением порядка 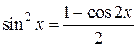, будем иметь: .

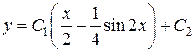Общее решение имеет вид .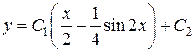

Пример 3. Найти общее решение дифференциального уравнения .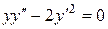

В этом уравнении в явном виде не содержится 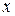, поэтому можно понизить порядок дифференциального уравнения.

Обозначим 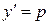, тогда 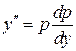. Подставляя эти выражения в исходное уравнение, получим 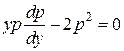, т.е. 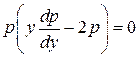. Уравнение распадается на два уравнения: 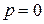и .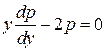

Для решения уравнения 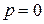запишем 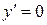, следовательно, .

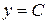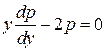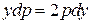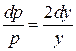Уравнение – уравнение с разделяющимися переменными: или , следовательно, 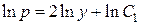. Потенцируя, получим 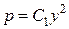, где 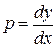. Интегрируя 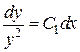, получим 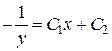или в явном виде .

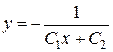Общее решение имеет вид .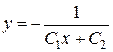

Линейные однородные уравнения n-го порядка

с постоянными коэффициентами

Это уравнения вида

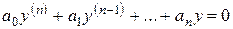, (4)

где 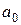, , 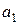,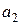…, 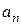– постоянные, .

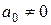Решение. 1. Составляем характеристическое уравнение

.

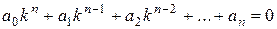Это алгебраическое уравнение будет иметь 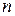корней.

2. Находим корни .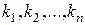

3. По характеру корней выписываем фундаментальную систему решений (ФСР), руководствуясь следующим:

а) каждому действительному однократному корню 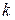соответствует решение .

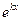б) каждой паре комплексно сопряженных корне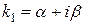й и 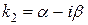соответствуют два частных решения 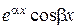и ;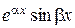

в) каждому действительному корню 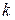кратности 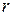соответствует 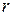линейно независимых частных решений .

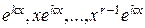г) каждой паре комплексных сопряженных корне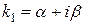й и 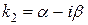кратности 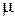соответствуют 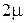частных решений:

, .

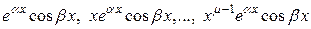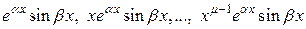ФСР состоит из 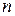составляющих ( 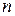– порядок уравнения (4), или степень характеристического уравнения). Эти решения линейно независимы.

4. Найдя 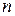линейно независимых решений 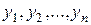, строим общее решение данного линейного уравнения 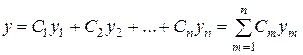, где 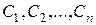– произвольные постоянные.

Пример 4. .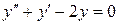

1. Составим характеристическое уравнение: .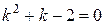

2. Находим корн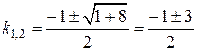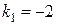и: , и .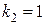

3. Корню 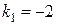соответствует решение 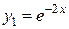, а корню 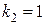– решение .

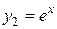4. Записываем общее решение данного дифференциального уравнения: 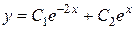, 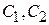-произвольные постоянные.

Пример 5. .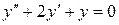

1. Составим характеристическое уравнение: .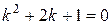

2. Находим корни: 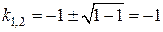, т.е. 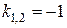– корни совпадают, значит, корень 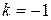– двукратный .

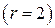3. Корню 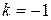кратности 2 соответствует два линейно независимых решения 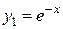и .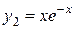

4. Записываем общее решение однородного дифференциального уравнения .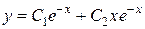

Пример 6. .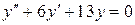

1. Составим характеристическое уравнение: .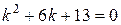

2. Находим корни: .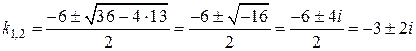

3. 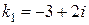, 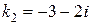– пара комплексно-сопряженных корней кратности 1, им соответствуют два частных линейно независимых решения: 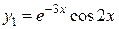и .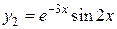

4. Записываем общее решение данного дифференциального уравнения: .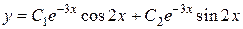

Пример 7. .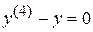

1. Составим характеристическое уравнение: .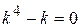

2. Находим корни: .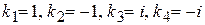

3. Записываем общее решение данного дифференциального уравнения: 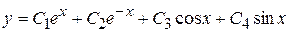.